算法设计与分析——贪心算法——活动安排问题

问题描述：设有n个活动的集合E={1,2,…,n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si<fi 。
如果选择了活动i，则它在半开时间区间[si, fi)内占用资源。

贪心算法总是做出在当前看来是最好的选择，也就是说，贪心算法并不从整体最优上加以考虑，所做出的的选择只是某种意义上的局部最优选择；
虽然贪心算法不是对所有的问题都能得到整体最优解，但对范围相当广的许多问题都能产生最优解，即使贪心算法不能得到整体最优解，但其最终结果却是最终结果却是最优解的很好的近似解。

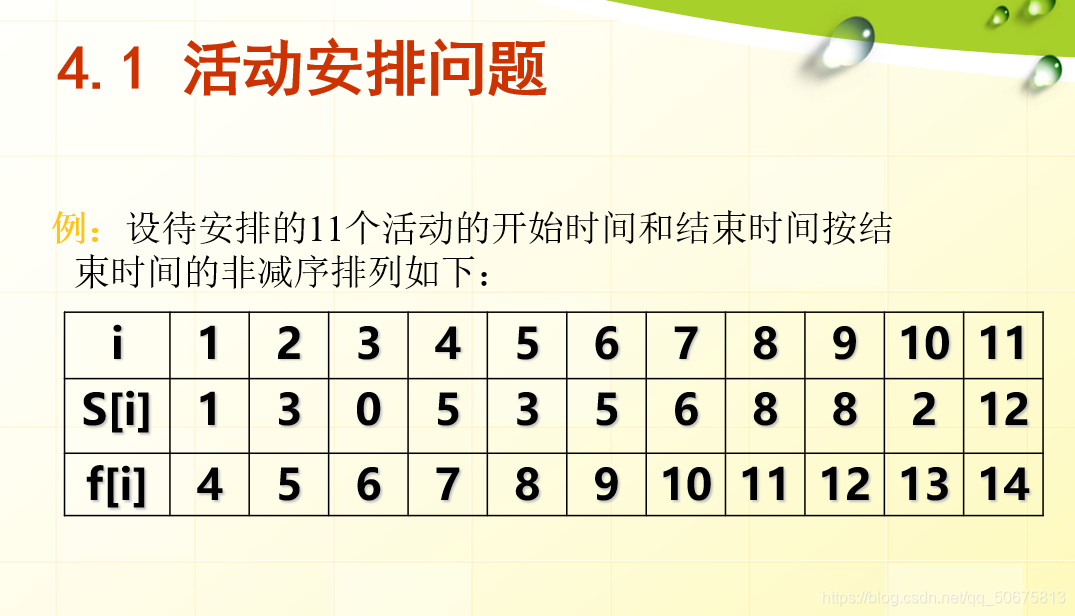
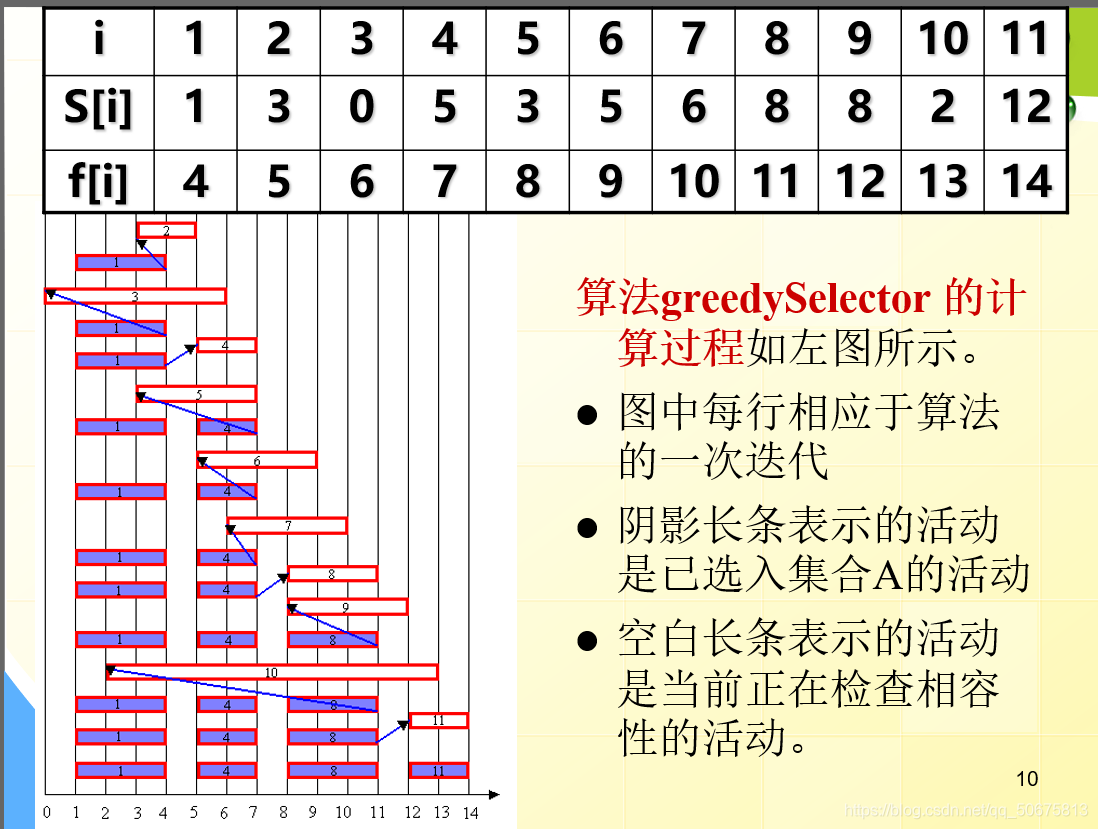
将活动按照结束时间进行从小到大排序。然后用i代表第i个活动，s[i]代表第i个活动开始时间，f[i]代表第i个活动的结束时间。按照从小到大排序，挑选出结束时间尽量早的活动，并且满足后一个活动的起始时间晚于前一个活动的结束时间，全部找出这些活动就是最大的相容活动子集合。

#include<iostream>
using namespace std;

void activity_arrangement(int n,int start[],int final[],bool result[])
{
   
   		//先按活动的结束时间排好序 
	int temp;
	 result[1]=true;
	 temp=1;
	 for(int i=2;i<=n;i++)
	 {
   
   
	 	if(final[temp]<=start[i])
	 	{
   
   
	 		result[i]=true;
	 		temp=i;
		}
		else
		{
   
   
			result[i]=false;
		}
	 }
	 
}

int main()
{
   
   
	int n;
	cout<<"输入活动的个数：";
	cin>>n; 
	
	int start[n+1];
	int final[n+1];
	cout<<"输入活动的开始时间序列：";
	for(int i=1;i<=n;i++)
	{
   
   
		cin>>start[i];
	}
	
	cout<<"输入活动的结束时间序列：";
	for(int i=1;i<=n;i++)