
**汉诺塔问题:**古代有一个梵塔,塔内有三个座A、B、C,A座上有64个盘子,盘子大小不等,大的在下,小的在上(如图)。有一个和尚想把这64个盘子从A座移到B座,但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘子始终保持大盘在下,小盘在上。我们的移动盘子的步骤为:
• 如果只有 1 个盘子,则不需要利用C塔,直接将盘子从A移动到B。
• 如果有 2 个盘子,可以先将盘子2上的盘子1移动到C;将盘子2移动到B;将盘子1移动到B。这说明了:可以借助C将2个盘子从A移动到B。
以此类推,上述的思路可以一直扩展到 n 个盘子的情况,将将较小的 n-1个盘子看做一个整体,也就是我们要求的子问题,以借助B塔为例,可以借助空塔B将盘子A上面的 n-1 个盘子从A移动到B;将A最大的盘子移动到C,A变成空塔;借助空塔A,将B塔上的 n-2 个盘子移动到A,将B最大的盘子移动到C,B变成空塔…
#include<bits/stdc++.h>
using namespace std;
int i = 1;
void move(char x,char y)
{
cout << "第"<<setw(4)<<i++<<"步,将盘子从" << x << "移动到" << y << endl;
}
void hanoi(int n,char a,char b,char c)
{
if(n>0)
{
hanoi(n - 1, a, c, b);
move(a, b);
hanoi(n - 1, c, b, a);
}
}
int main()
{
int n;
cout<<"请输入要进行hanoi问题的层数:"<<endl;
cin>>n;
hanoi(n, 'a', 'b', 'c');
system("pause");
return 0;
}
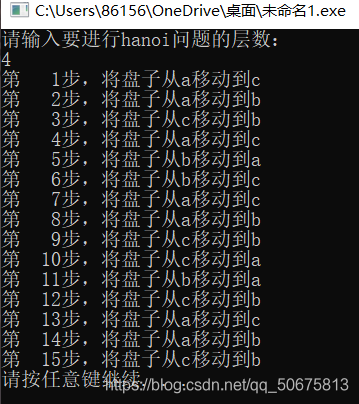





 本文详细介绍了汉诺塔问题的解决方案,通过递归算法实现将64个盘子从A座移动到B座的过程。文章首先阐述了问题的基本规则,然后逐步解析如何借助第三个座C来完成移动。最后,给出了C++代码实现,演示了如何用程序解决这一经典问题。
本文详细介绍了汉诺塔问题的解决方案,通过递归算法实现将64个盘子从A座移动到B座的过程。文章首先阐述了问题的基本规则,然后逐步解析如何借助第三个座C来完成移动。最后,给出了C++代码实现,演示了如何用程序解决这一经典问题。

















 2181
2181

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








