
#include<stdio.h>
#include<string.h>
#define INF 32767
#define MAXVEX 30
int dist[MAXVEX]; //建立dist数组
int path[MAXVEX]; //建立path数组
int S[MAXVEX]; //建立S数组
typedef char VertexType;
typedef struct graph
{
int n,e;
VertexType vexs[MAXVEX];
int edges[MAXVEX][MAXVEX];
}MGraph;
void CreateMGraph(MGraph &G)
{
int n,e;
int value;
char temp_i;
char temp_j;
printf("请输入图的顶点数和边数(以空格分隔):");
scanf("%d%d",&n,&e);
G.n=n;G.e=e;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(i==j)
G.edges[i][j]=0;
else
G.edges[i][j]=32767;
}
}
printf("输入顶点信息:");
for(int j=0;j<G.n;j++)
{
getchar();
scanf("%c",&G.vexs[j]);
}
int temp_number_i;
int temp_number_j;
printf("请输入每条边的权值:\n");
for(int j=0;j<e;j++)
{
getchar();
scanf("%c %c %d",&temp_i,&temp_j,&value);
for(int i=0;i<n;i++)
{
if(G.vexs[i]==temp_i)
temp_number_i=i;
if(G.vexs[i]==temp_j)
temp_number_j=i;
}
G.edges[temp_number_i][temp_number_j]=value;
}
}
void DispMGraph(MGraph &G)
{
printf("输出顶点信息:\n");
for(int i=0;i<G.n;i++)
{
printf("%c",G.vexs[i]);
}
printf("\n输出邻接矩阵:\n");
printf("\t");
for(int i=0;i<G.n;i++)
printf("%8c",G.vexs[i]);
for(int i=0;i<G.n;i++)
{
printf("\n%8c",G.vexs[i]);
for(int j=0;j<G.n;j++)
{
if(G.edges[i][j]==32767)
//两点之间无连接时权值为默认的32767,
// 在无向图中一般用"0"表示,在有向图中一般用"∞",
// 这里为了方便统一输出 "∞"
printf("%8s", "∞");
else
printf("%8d",G.edges[i][j]);
}
printf("\n");
}
}
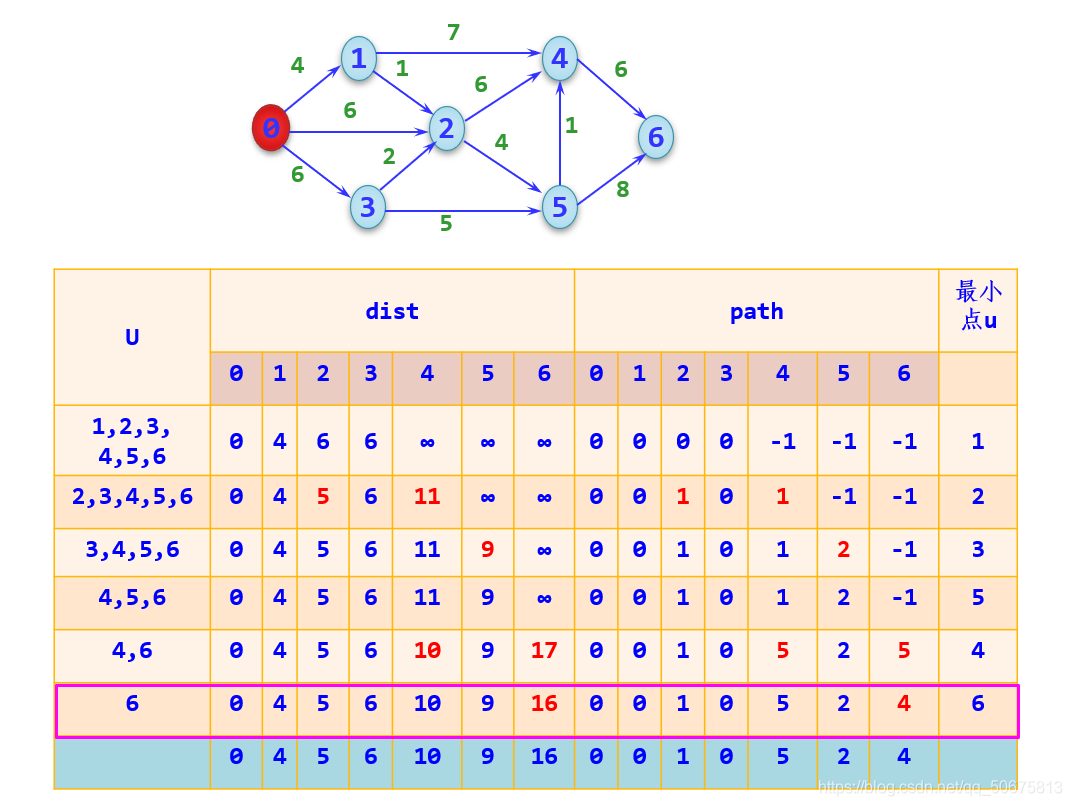
void Dijkstra(MGraph g, int v)
{
//求从v到其他顶点的最短路径
int mindis,i,j,u=0;
for (i=0;i<g.n;i++)
{ dist[i]=g.edges[v][i]; //距离初始化
S[i]=0; //S[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v; //v→i有边时,置i前一顶点为v
else //v→i没边时,置i前一顶点为-1
path[i]=-1;
}
S[v]=1; //源点编号v放入S中
for (i=0;i<g.n-1;i++) //循环向S中添加n-1个顶点
{ mindis=INF; //mindis置最小长度初值
for (j=0;j<g.n;j++) //选取不在S中且有最小距离顶点u
if (S[j]==0 && dist[j]<mindis)
{ u=j;
mindis=dist[j];
}
S[u]=1; //顶点u加入S中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (S[j]==0)
if (g.edges[u][j]<INF
&& dist[u]+g.edges[u][j]<dist[j])
{ dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
}
void Print(MGraph G,int v)
{
printf("\n");
for(int i=0;i<G.n;i++){
if(i!=v && dist[i]!=INF){
printf("%c到%c的最短距离为:%d\n",G.vexs[v],G.vexs[i],dist[i]);
}else if(dist[i]==INF){
printf("%c与%c之间无路径!\n",G.vexs[v],G.vexs[i]);
}
}
printf("\n");
}
/*------------------输出从顶点v出发的所有最短路径-------------------*/
static void Dispath(MGraph g, int v)
{
int i, j, k;
int apath[MAXVEX], d; //存放一条最短路径(逆向)及其顶点个数
//循环输出从顶点v到i的路径
for(i = 0; i < g.n; i++)
{
if(S[i] == 1 && i != v)
{
printf("从顶点%c到顶点%c的路径长度为:%d\t路径为:", g.vexs[v], g.vexs[i], dist[i]);
d = 0; apath[d] = i; //添加路径上的终点
k = path[i];
if(k == -1) //没有路径的情况
printf("无路径\n");
else //存在路径时输出该路径
{
while(k != v)
{
d++;
apath[d] = k;
k = path[k];
}
d++; apath[d] = v; //添加路径上的起点
printf("%c ", g.vexs[apath[d]]); //先输出起点
for(j = d - 1; j >= 0; j--) //再输出其余顶点
printf(" %c ", g.vexs[apath[j]]);
printf("\n");
}
}
}
}
static void Dispath2(MGraph g, int v,int w)
{
int i, j, k;
int apath[MAXVEX], d; //存放一条最短路径(逆向)及其顶点个数
//循环输出从顶点v到i的路径
for(i = 0; i < g.n; i++)
{
if(S[i] == 1 && i != v&&i==w)
{
printf("%d\n",dist[i]);
d = 0; apath[d] = i; //添加路径上的终点
k = path[i];
if(k == -1) //没有路径的情况
printf("无路径\n");
else //存在路径时输出该路径
{
while(k != v)
{
d++;
apath[d] = k;
k = path[k];
}
d++; apath[d] = v; //添加路径上的起点
printf("%c ", g.vexs[apath[d]]); //先输出起点
for(j = d - 1; j >= 0; j--) //再输出其余顶点
printf(" %c ", g.vexs[apath[j]]);
printf("\n");
}
}
}
}
void min_shortest_path(MGraph G,int v)
{
int mindist=dist[0];
int temp;
for(int i=1;i<G.n;i++)
{
if(mindist<dist[i])
{
mindist=dist[i];
temp=i;
}
}
printf("图中距离顶点%c最短路径长度中最大的为:",G.vexs[v]);
Dispath2(G, v,temp);
}
int main()
{
MGraph G;
CreateMGraph(G);
DispMGraph(G);
Dijkstra(G,0);
Print(G,0);
Dispath(G,0);
min_shortest_path(G,0);
}





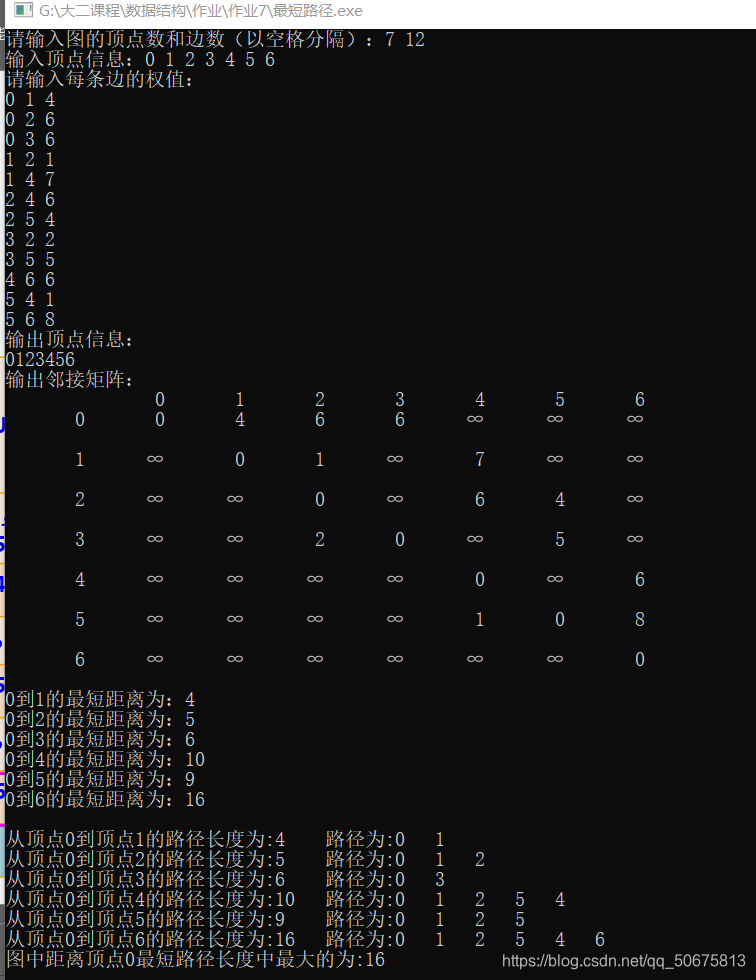
 本文介绍了一种使用C语言实现迪杰斯特拉算法的方法,该算法用于寻找加权图中两点之间的最短路径。文章详细展示了如何创建图的数据结构、输入顶点和边的信息,并通过示例演示了如何计算和输出所有顶点间的最短路径。
本文介绍了一种使用C语言实现迪杰斯特拉算法的方法,该算法用于寻找加权图中两点之间的最短路径。文章详细展示了如何创建图的数据结构、输入顶点和边的信息,并通过示例演示了如何计算和输出所有顶点间的最短路径。

















 700
700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








