数据结构：二叉树层序遍历和判断是否为完全二叉树

层序遍历

从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第二层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的节点的过程。

while(队列！=NULL)
{
1.从空间中取出一个节点cur，进行遍历
2.如果cur有左孩子，将其保存
3.如果cur有右孩子，将其保存
4.将刚刚遍历的节点从空间中删除掉
}

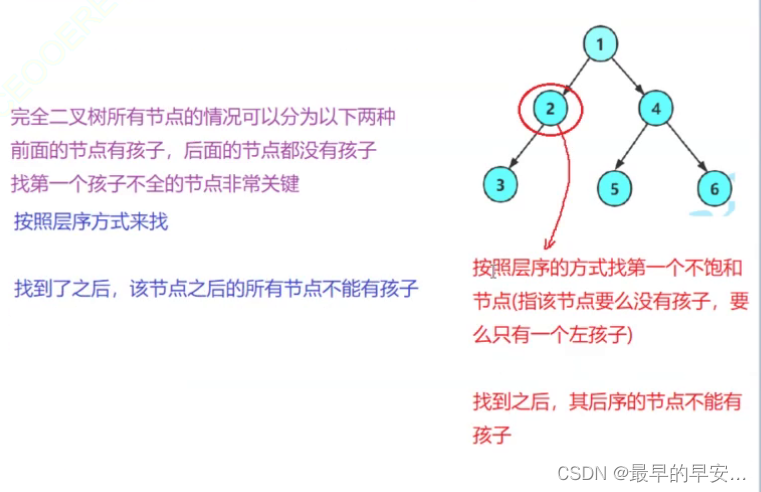
判断是否为完全二叉树

#include<stdio.h>
#include<assert.h> 
#include<stdlib.h>

typedef struct BTNode
{
    struct BTNode* left;
    struct BTNode* right;
    int data;
}BTNode;

typedef struct BTNode* QDataType;

typedef struct QNode
{
	QDataType data;
	struct QNode* next;
}QNode;

//队列的结构
typedef struct Queue
{
	QNode* front;   //指向队头
	QNode* back;    //指向队尾
}Queue;
//队列结构初始化
void QueueInit(Queue* q)
{
	assert(q);
	q->front = NULL;
	q->back = NULL;
}
//队列删除元素(头删)
void QueuePop(Queue* q)
{
	assert(q);
	//空链表,直接返回
	if (QueueEmpty(q))
	{
		return;
	}
	//只有一个节点
	else if (q->front == q->back)
	{
		free(q->front);
		q->front = NULL;
		q->back = NULL;
	}
	//多个节点（头删）
	else
	{
		QNode* delNode = q->front;
		q->front = q->front->next;
		free(delNode);
	}
}
//队列是否为空
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->front == NULL;
}
//查询队头(保证必须有元素)
QDataType QueueFront(Queue* q)
{
	assert(q);
	return q->front->data;
}
//销毁队列(头删)
void QueueDestroy(Queue* q)
{
	QNode* cur = q->front;
	while (cur)
	{
		q->front = q->front->next;
		free(cur);
		cur = q->front;
	}
	//当所有元素删完，队列成为空队列
	q->front = NULL;
	q->back = NULL;
}
//二叉树层序遍历
void BinaryLevelOrder(BTNode* root)
{
    if (root == NULL)
        return;
    //层序遍历需要借助队列
    Queue q;
    QueueInit(&q);
    //将树的根节点如果队列，然后当队列不空时，循环进行操作
    QueuePush(&q, root);
    while (!QueueEmpty(&q))
    {
        struct BTNode* cur = QueueFront(&q);
        //将该节点遍历
        printf("%d", cur->data);
        //如果cur有左孩子则入队，如果有右孩子则入队
        if (cur->left)
            QueuePush(&q, cur->left);
        if (cur->right)
            QueuePush(&q, cur->right);
        QueuePop(&q);
    }
    QueueDestroy(&q);
    printf("/n");
}

//是否为完全二叉树
int BinaryTreeComplete(BTNode* root)
{
    //空树也是完全二叉树
    if (root = NULL)
        return 1;
    //按照层序遍历的方式找到第一个不饱和的节点
    Queue q;
    int flag = 0;//标记第一个不饱和节点的位置
    int CompleteTree = 1;
    QueueInit(&q);
    QueuePush(&q, root);
    while (QueueEmpty(&q))
    {
        BTNode* cur = QueueFront(&q);
        QueuePop(&q);//队列中删除
        if (flag)//找到第一个不饱和节点
        {
            //不饱和节点之后所有的节点不能有孩子
            if (cur->left || cur->right)
            {
                CompleteTree = 0;
                break;
            }
        }
        else//寻找第一个不饱和节点
        {
            //检测cur是否为饱和的节点：一个的两个孩子为饱和节点
            if (cur->left && cur->right)
            {
                QueuePush(&q, cur->left);
                QueuePush(&q, cur->right);
            }
            else if (cur->left)//只有左孩子
            {
                //找到第一个不饱和节点
                QueuePush(&q, cur->left);
                flag = 1;
            }
            else if (cur->right)//只有右孩子
            {
                CompleteTree = 0;
                break;
            }
            else//cur左右孩子都不存在 
            {
                flag = 1;
            }
        }
    }
    QueueDestroy(&q);
    return CompleteTree;
}