完全二叉树与堆-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_50426849/article/details/127078120

堆

1.首先是完全二叉树（可以使用顺序结构存储）
2.完全二叉树的节点必须满足：
a.如果任意节点都比其孩子节点小，将其称为小堆（小根堆）
b.如果任意节点都比其孩子节点大，将其称为小堆（大根堆）
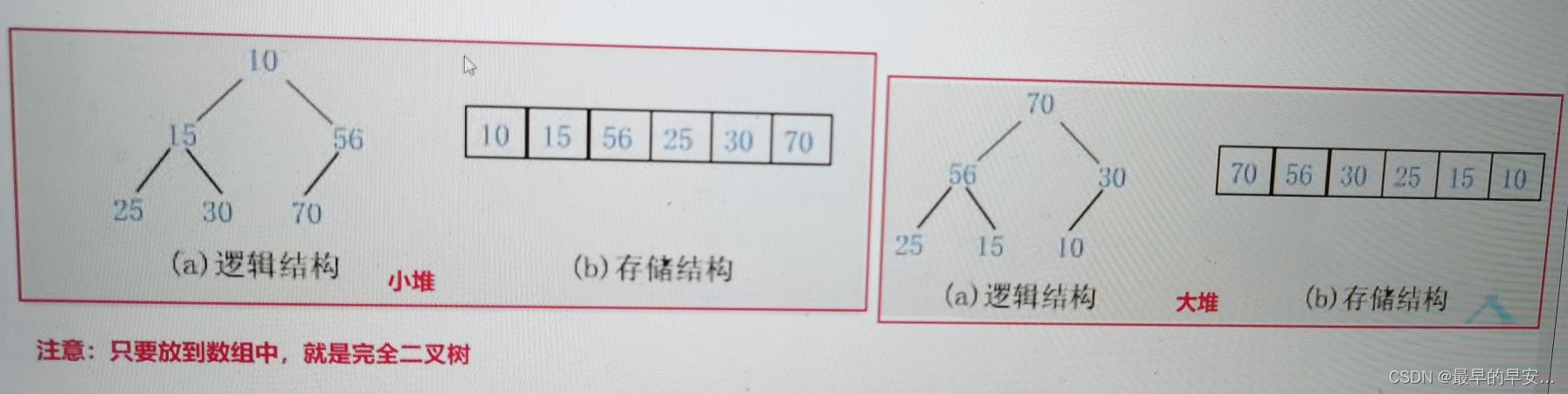
在这里插入图片描述

堆的特性

1.堆顶元素是集合中最大或最小的元素
2.堆中：任意节点都比其孩子节点大或小
3.从堆顶到任意孩子节点路径中所经的节点是降序或升序。

将完全二叉树转换为堆
在这里插入图片描述

//将完全二叉树转换为堆

void AdjustDown(int array[],int size,int parent)
{
 int child = parent*2+1;//优先让child标记左孩子
 while(child<size)
 {
//需要检测parent是否满足堆的特性
//与其孩子比较，如果不满足则交换：一定要较小的孩子
   if(array[child+1]<array[child])
    child=child+1;
//再检验双亲和较小孩子的关系，不满足则交换
   if(array[child]<array[parent])
  {
  Swap(&array[child],&array[parent]);
  //大的元素往下移动，可能会导致子树不满足堆特性
  parent = child;
  child = parent*2+1;
   }
   else 
     return;  
 }
}