动态规划讲解

动态规划

思维导图

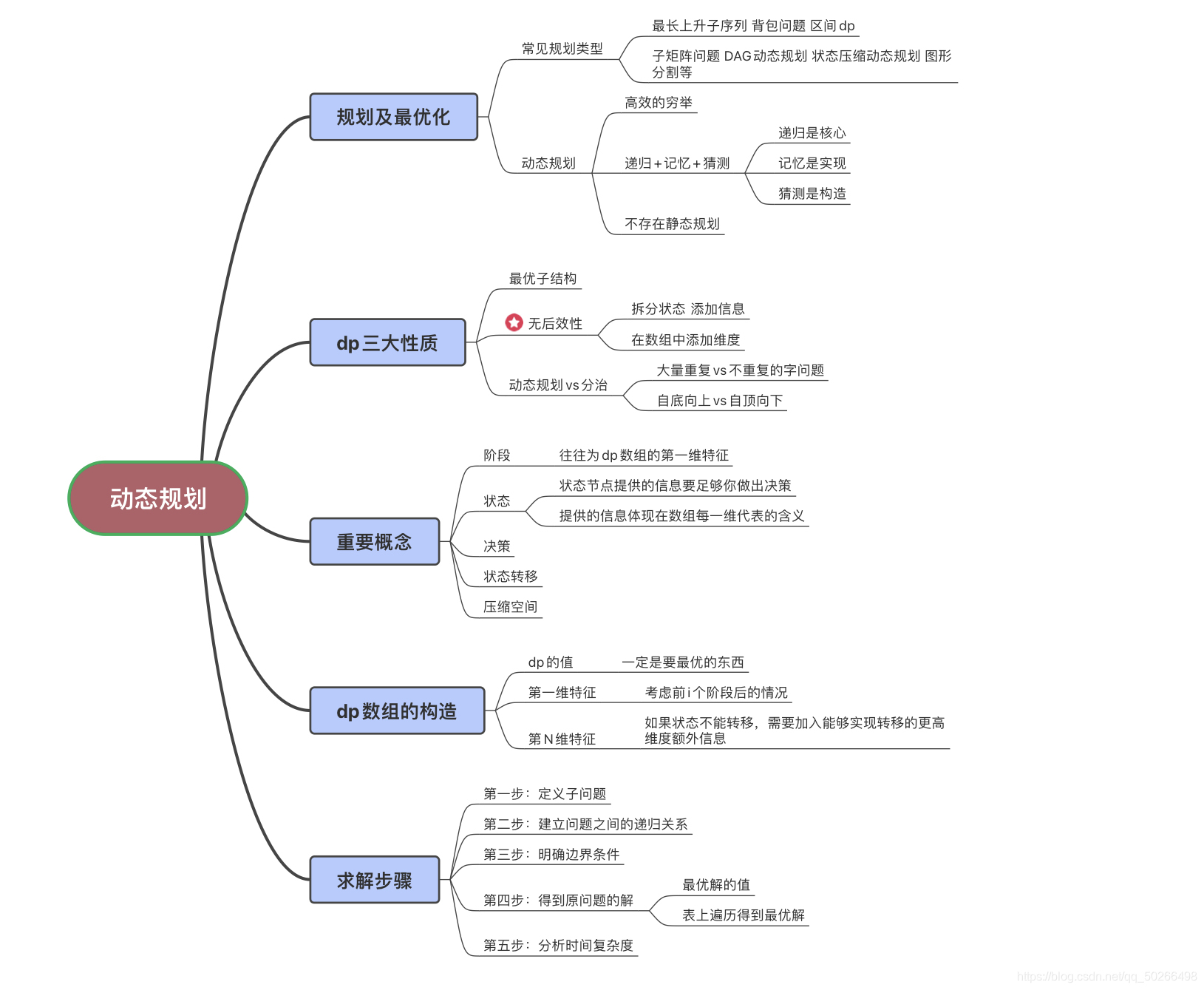
例题 最长公共子序列

1. 题目描述
   最长公共子序列问题，给定序列X=<x1,x2,…,xm>，Y=<y1,y2,…,yj>，求X和Y的最长公共子序列。
   设X和Z是两个序列，其中X=<x1,x2,…,xm>，Z=<z1,z2,…,zk>，如果存在X的元素构成的按下标严格排序递增序列<xi1,xi2,…,xik>，使得xij=zj，j=1,2,…,k，那么Z是X的子序列，Z含有的元素个数，称为子序列的长度。
   定义：设X和Y是两个序列，如果Z既是X的子序列，也是Y的子序列，则称Z是X和Y的公共子序列。

2. 解析
   Xi=<x1,x2,…,xi>
   Yj=<y1,y2,…,yj>
   Zk=<z1,z2,…,zk>
   如果Zk是Xi和Yj的最长公共子序列，
   （1）xi = yj，那么zk = xi = yj，Zk-1是Xi-1和Yj-1的最长公共子序列
   （2）xi ≠ yj，那么zk ≠ xi，Zk-1是Xi-1和Yj的最长公共子序列
   （3）xi ≠ yj，那么zk ≠ yi，Zk-1是Xi和Yj-1的最长公共子序列

3. 最优子结构和重叠子问题

最优子结构
设 X=(x1,x2,…xn) 和 Y={y1,y2,…ym} 是两个序列，将 X 和 Y 的最长公共子序列记为c(X,Y)，找出c(X,Y)就是一个最优化问题。因为，我们需要找到X 和 Y中最长的那个公共子序列。而要找X 和 Y的c，首先考虑X的最后一个元素和Y的最后一个元素。
1）如果 xn=ym，即X的最后一个元素与Y的最后一个元素相同，这说明该元素一定位于公共子序列中。因此，现在只需要找：c(Xn-1，Ym-1)。c(Xn-1，Ym-1)就是原问题的一个子问题。为什么叫子问题？因为它的规模比原问题小。为什么是最优的子问题？因为我们要找的是Xn-1 和 Ym-1 的最长公共子序列。
2）如果xn != ym，这下要麻烦一点，因为它产生了两个子问题：c(Xn-1，Ym) 和 c(Xn，Ym-1)，因为序列X 和 序列Y 的最后一个元素不相等嘛，那说明最后一个元素不可能是最长公共子序列中的元素嘛。c(Xn-1，Ym)表示：最长公共序列可以在(x1,x2,…x(n-1)) 和 (y1,y2,…ym)中找。而c(Xn，Ym-1)表示：最长公共序列可以在(x1,x2,…xn) 和 (y1,y2,…y(m-1))中找。
求解上面两个子问题，得到的公共子序列谁最长，那谁就是 c（X,Y）。用数学表示就是：
c=max{c(Xn-1，Ym)，c(Xn，Ym-1)}
由于条件 1) 和 2) 考虑到了所有可能的情况。因此，我们成功地把原问题转化 成了 三个规模更小的子问题。

重叠子问题
重叠子问题是啥？就是说原问题转化成子问题后，子问题中有相同的问题。
在此题中原问题是：c(X,Y)。子问题有 ❶c(Xn-1，Ym-1) ❷c(Xn-1，Ym) ❸c(Xn，Ym-1)。

初一看，这三个子问题是不重叠的。可本质上它们是重叠的，因为它们只重叠了一大部分。举例：第二个子问题：c(Xn-1，Ym) 就包含了：问题❶c(Xn-1，Ym-1)。因为，当Xn-1 和 Ym 的最后一个元素不相同时，我们又需要将c(Xn-1，Ym)进行分解：分解成：c(Xn-1，Ym-1) 和 c(Xn-2，Ym)。
也就是说：在子问题的继续分解中，有些问题是重叠的。

4. 状态转移方程
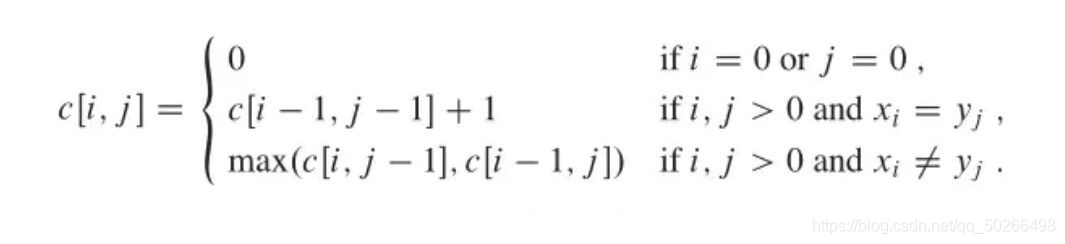
   *其中c[i,j]表示a串的前i项与b串的前j项的最长公共子序列

5. 代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int c[100][100],s[100][100];
void game(char *a,char *b,int m,int n);
void lcs(char *a,int i,int j);
int main()
{
​int n;
​scanf("%d",&n);
​getchar();
​while(n--)
​{
​char a[100];
​char b[100];
​gets(a);
​gets(b);
​int s1=strlen(a);
​int s2=strlen(b);
​game(a,b,s1-1,s2-1);
​}
​return 0;
}
void game(char *a,char *b,int m,int n)
{
​for(int i=0;i<=m;i++)
​c[i][0]=0;
​for(int i=0;i<=n;i++)
​c[0][i]=0;
​for(int i=0;i<=m;i++)
​for(int j=0;j<=n;j++)
​{
​if(a[i]==b[j])
​{
​c[i][j]=c[i-1][j-1]+1;
​s[i][j]=1;
​}
​else if(c[i-1][j]>c[i][j-1])
​{
​c[i][j]=c[i-1][j];
​s[i][j]=2;
​}
​else
​{
​c[i][j]=c[i][j-1];
​s[i][j]=3;
​}
​}
​printf("%d\n",c[m][n]);
​lcs(a,m,n);
​printf("\n");
}
void lcs(char *a,int i,int j)
{
​if(s[i][j]==1)
​{
​lcs(a,i-1,j-1);
​printf("%c",a[i]);
​ }
​ else if(s[i][j]==2)
​ ​lcs(a,i-1,j);
​ ​else if(s[i][j]==3)
​ ​lcs(a,i,j-1);
}

点击查看博客内容