图像拼接-APAP算法精读As-Projective-As-Possible Image Stitching with Moving DLT-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_48625029/article/details/144412350

主要思想：

使用单一的全局投影矩阵，只能应对平面场景的图像拼接，对于有视差的图像拼接，结果会有鬼影（ghosting artefacts）。作者针对这一问题，提出了将图像网格化，然后利用Moving DLT的获得每个网格的投影矩阵。

原文内容：“目前的大多数技术（包括Autostitch和Photosynth）将对齐函数建模为2D投影变换或同形变换（同形变换就是homography-单应矩阵）。只有当图像对应于纯粹因旋转而不同的视图时，或者如果成像的场景实际上是平面的（例如，当场景足够远时），单应矩阵的做法才被证明是合理的”

理解：首先来看单应矩阵的定义。单应矩阵可以理解为有2台相机，从不同的视角看同一个二维平面。如下图。

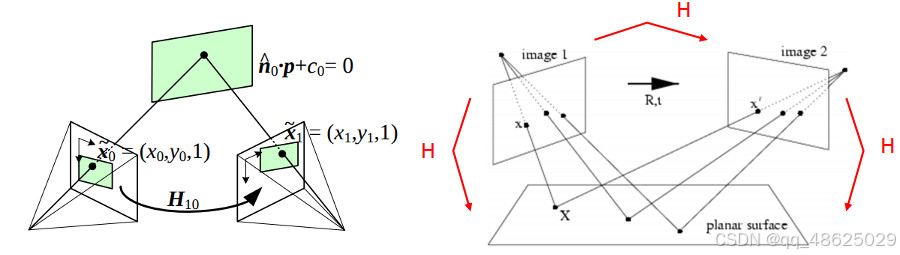
假设该二维平面上有一个点，落在相机A上的坐标为（x,y），落在相机B上的坐标为（x',y'），那么这2个点可以通过单应矩阵H进行映射。

由于观测对象是在同一平面，所以物体上的点都在同一平面上。只有当物体是平面，相机内参已知的情况下，相机的姿态才可以从单应矩阵中估计出来。到这里就可以得出结论了，因为转换的矩阵公式就是只针对二维平面的，所以在三维世界中存在缺陷。

超定方程组是指方程的个数多于未知数的个数的方程组，通常没有精确解。在这种情况下，最小二乘法提供了一种寻找最佳近似解的方法。这种方法的目标是最小化残差平方和，即找到参数，使得所有方程的残差（实际观测值与模型预测值之间的差异）的平方和最小。

求解出H之后，源图像中的点x就可以通过变换得到对应的位置x'=Hx

使用上一部分推导的普通投影变换，无法处理复杂场景，比如不是单纯旋转或者2个视角不在同一平面的时候，存在视差的情况下就会产生重影。为了解决这个问题，每一个网格使用一个独立的局部单应。其实就是多加了一个权重W，之前是Ah,现在是WAh，权重由每个像素与该像素格子左上角的距离确定。

在前面已经提到过，因为计算每个像素非常浪费，所以分块。

观察到许多权重 wi∗ 接近于一个偏移值 γ，这意味着许多权重实际上是相同的。因此，可以利用这个性质来更新WSVD，而不是从头开始计算。