求解方程(2x^3) +(4x^2)+3x-6=0
牛顿迭代法
牛顿迭代法公式:(以下图片均来源于百度)
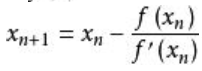
牛顿迭代法用递归实现解三元一次方程:
#include<stdio.h>
#include<math.h>
int main(){
int fx(double x1);
double x1=1.5;
printf("%.2f",fx(x1));
return 0;
}
int fx(double x1)
{
//X0为公式中的Xn,f表示f(Xn),fl表示f(Xn)的导数
double x0, f, fl;
//将求出的新X1赋值给X0
x0 = x1;
f = (2 * pow(x0, 3) - 4 * pow(x0, 2) + 3 * x0 - 6);
fl = (6 * pow(x0, 2) - 8 * x0 + 3);
x1 = x0 - f / fl;
//调自己实现迭代(即递归),当等于0时,求出值
if(fx(x1)==0)return x1;
}
二分法解方程
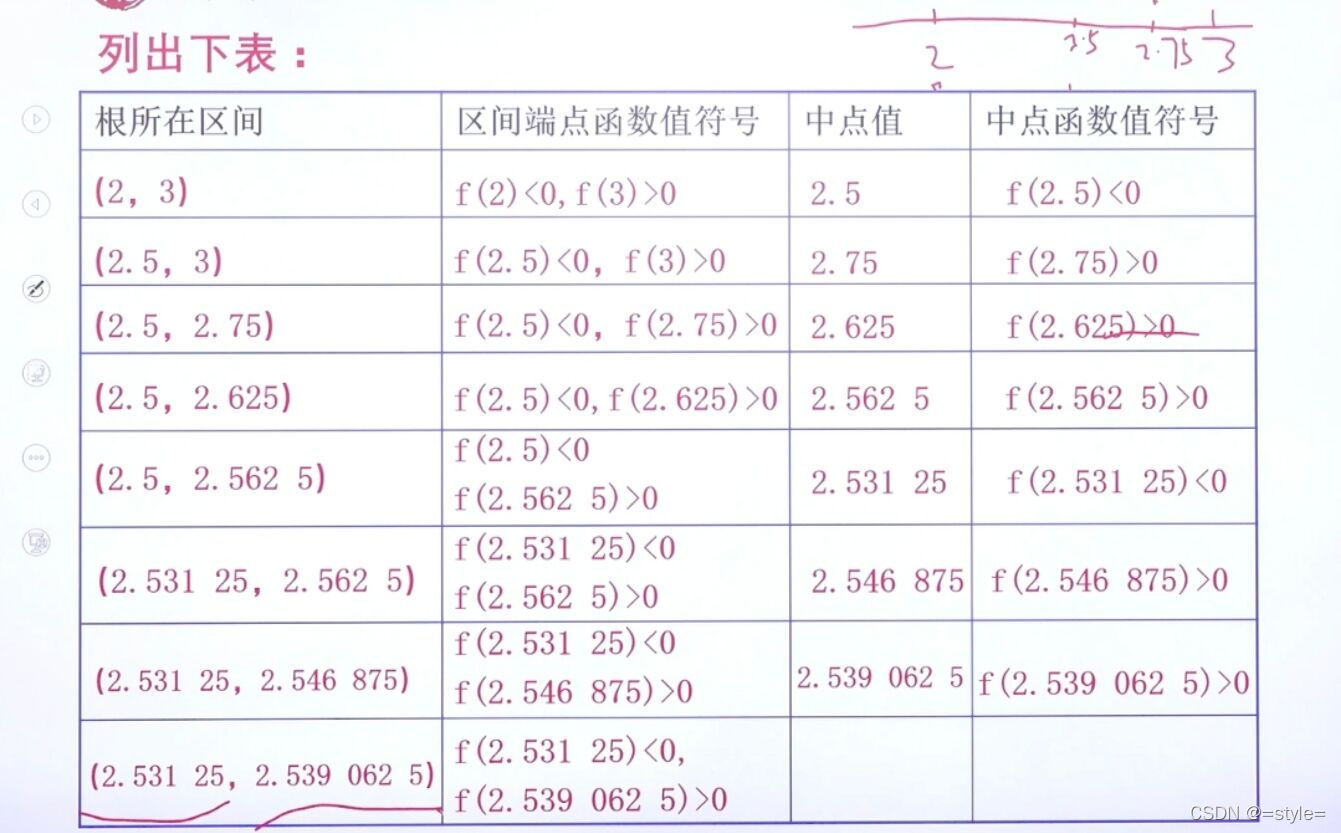
二分法用递归实现解三元一次方程:
#include <stdio.h>
#include <math.h>
double fun(double low, double high);
int main()
{
printf("%.2f", fun(-10, 10));
return 0;
}
double fun(double low, double high)
{
double mid,fm;
mid = (low + high) / 2;
fm = 2 * pow(mid, 3) - 4 * pow(mid, 2) + 3 * mid - 6;
if ((high-low)>1e-5)
{
if (fm < 0)
low = mid;
else if (fm > 0)
high = mid;
else return mid;
return fun(low, high);
}
return mid;
}








 这篇博客介绍了如何运用牛顿迭代法和二分法来解三次方程,提供了C语言实现的代码示例,分别展示了这两种数值方法在解决(2x^3)+(4x^2)+3x-6=0这个具体方程时的过程。通过递归迭代,找到方程的根。
这篇博客介绍了如何运用牛顿迭代法和二分法来解三次方程,提供了C语言实现的代码示例,分别展示了这两种数值方法在解决(2x^3)+(4x^2)+3x-6=0这个具体方程时的过程。通过递归迭代,找到方程的根。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










