图的两种遍历方法

图的遍历

图的遍历是指，从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历。

图的遍历过程根据搜索方法的不同，又可划分为两种搜索策略

1.深度优先遍历
2.广度优先遍历

算法思想

1.深度优先遍历（dfs）

深度优先遍历的步骤

• 访问顶点V
• 依次从顶点V的未被访问的邻节点出发，进行深度优先搜索，直至和V有路径相通的顶点都被访问到。
• 对于连通图进行遍历时，从一个顶点出发即可访问图中所有的顶点。
• 对于非连通图进行遍历时，若图中尚有顶点未被访问，则另选一未曾访问的顶点作为起始点，进行深度优先搜索，直至所有顶点都被访问

访问过程如图所示

遍历结果：v1,v2,v4,v8,v5,v3,v6,v7,v9,v10

2.广度优先遍历

从顶点V出发广度优先搜索的步骤

• 访问顶点V
• 依次访问顶点V的各个未被访问的临接点（横向访问）
• 从V的这些邻接点出发依次访问他们的邻接点，致使“先被访问的顶点的邻接点先于"后访问的顶点的邻接点"被访问，直至图中所有已被访问的顶点的邻接点均被访问。
• 对于非连通图进行遍历时，若图中尚有顶点未被访问，则另选一未曾访问的顶点作为起始点，进行广度优先搜索，直至所有顶点都被访问
  遍历的过程：
  
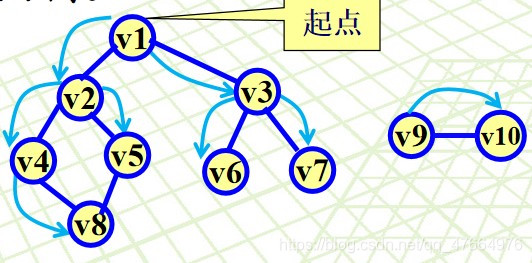
  遍历的结果：V1,V2,V3,V4,V5,V6,V7,V8,V9,V10

具体代码实现：

//深度优先搜索（DFS）
void DFS(AMGraph G, int v){
cout<<G.vex[v];
visit[v]=1;
for(j=0;j<G.vexnum;j++){
if(G.arcs[v][j]&&!visited[j]) DFS(G,j)
    }
}
void DFSTraverse(AMGraph G){
for(v=0;v<G.vexnum;v++) 
   visited[v]=0;
   for(v=0;v<G.vexnum;v++)
   if(!visited[v])DFS(G,v);
}



//广度优先搜索（BFS）
void BFSTracerse(AMGraph G){
for(v=0;v<G.vexnum;v++) visited[v]=0;
InitQueue(Q);
for(v=0;v<G.vexnum;v++){
     if(!visited[v])
     {
     cout<<G.vexs[v];  
     visited[v]=1;
     EnQueue(Q,v);
     while(!QueueEmpty(Q)){
     DeQueue(Q,u);
     for(j=0;j<G.vexnum;j++){
         if(G.arcs[u][j]==1&&!visited[j])
            {
                  cont<<G.vexs[j];
                  visited[j]=1;
                  EnQueue(Q,j);
                  }
                }
            }
        }
    }
}