信息安全数学基础知识点学习笔记（一）

第一章、整数的可除性

你好！ 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章，了解一下Markdown的基本语法知识。

整除的概念、欧几里得除法

整除的概念

梦的起点：整除的定义

定义1.1.1：设a,b是任意两个整数，其中b不为0，如果存在一个整数使得等式 a=q*b成立，就称为b整除a，或者a被b整除，记作 b|a ，并把b叫做a的因数，把a叫做b的倍数，人们长将q表示为 a/b ，否则就称b不能整除a，或a不能整除b记作b

整除的定义是信息安全数学的基础，之后的知识都建立在整除之上。

下面的是定义1的备注
同时

0是任何非零整数的倍数
1是任何整数的因数
任何非零整数a是其自身的倍数，也是自身的因数

反应一下就是，如果存在整除关系b|a，那么就有a=b*q，且q为一个整数。

定理1.1.1

设a，b，c不等于0，且都为整数，若 b|a , c|b ,那么c|a。（整除的传递性）

证明：

因为 c|b，b|a，有b=cq, a=bp
a=bp=(cq) p=cq
故c|a

定理1.1.2

设a, b, c≠0且是整数．若 c|a , c|b, 则 cl（a士b）.(加法运算)

证明：

因为c|a，c|b，有a=cq, b=cp
a士b= cq 士 cp =c(q 士p )
故c|a

定理1.1.3
定理1.1.4
实际上就是定理1.1.3的拓展定理1.1.5
以上说以定理皆可由整除的定义式证。

素数的概念

整除的提升：素数的定义

设整数n不等于0，正负1，如果除了显然因数：正负1,正负n以外，n没有其他因数，那么，n就叫做素数（或质数或不可约数），否则称为合数。

当没有特别申明的的时候，素数一般指的是正整数。

定理1.1.6
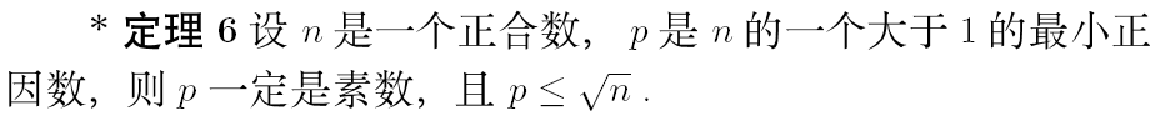证明

反证法：如果p不是素数，则有q，1<q<p, q|p ， q|n , 即n有小于p的正因数, 矛盾！

Eratoshenes筛法

当我们定义了整除，并依据整除的定义划分了素数与合数之后，自然而然的想法是，如何判断一个数是否是素数？这个时候希腊数学家埃拉托斯特尼提出了一种判断方法：即Eratoshenes筛法

定理1.1.7
证明：

用反证法, 设n是合数,取 p是n的大于1的最小正因数, 即p |n. 则由定理6, p 一定是素数, 与定理条件

那么知道了如何去判断一个数是否为素数之后，继续探索，在实数域内有多少素数呢？

定理1.1.8

证明：

反证法：假设只有有限个素数，设为：p1, p2…, pk
$n=p_1{p}_2\cdots p_k+1$
n>pi，n为合数，设最小素因子为p，p=pj
$p|n-p_1{p}_2\cdots p_k=1$
矛盾！故有无穷多个素数。

欧几里得除法——最小非负余数

因为并不是任意两个整数之间都是有整除关系的，因此我们引进欧几里得除法（也称为带余除法）
定理1.1.9
在有了带余除法之后，自然的，余下来的是什么呢？因此出现了定义1.1.3
定义1.1.3

定理1.1.9中的q称为a被b除所得的不完全商，r叫做a被b除的余数

由此我们可以将其与整除的概念相联系得到一个推论:
b整除于a的冲要条件是a被b除的余数为0

定义1.1.4

设x是实数，称x的整数部分为小于或等于x的最大整数，记为[x]，这时有
[x]<=x<[x]+1

素数的平凡判别

通过欧几里得除法与定理1.1.7，我们可以得到一个可以判断一个具体的数是否为素数的方法：

素数的平凡判别

对于给定的正整数N，设不大于根号N的所有素数p1…pn。如果N被所有pi除的余数都不为0，即pi不整除于n，那么N是素数。

欧几里得除法—— 一般余数

在实际运用欧几里得除法的时候，可以根据需求将余数取成其他形式。

定理1.1.10
一般来说对我们没有什么实质的影响，本质不变。
其余数的形式有很多种：

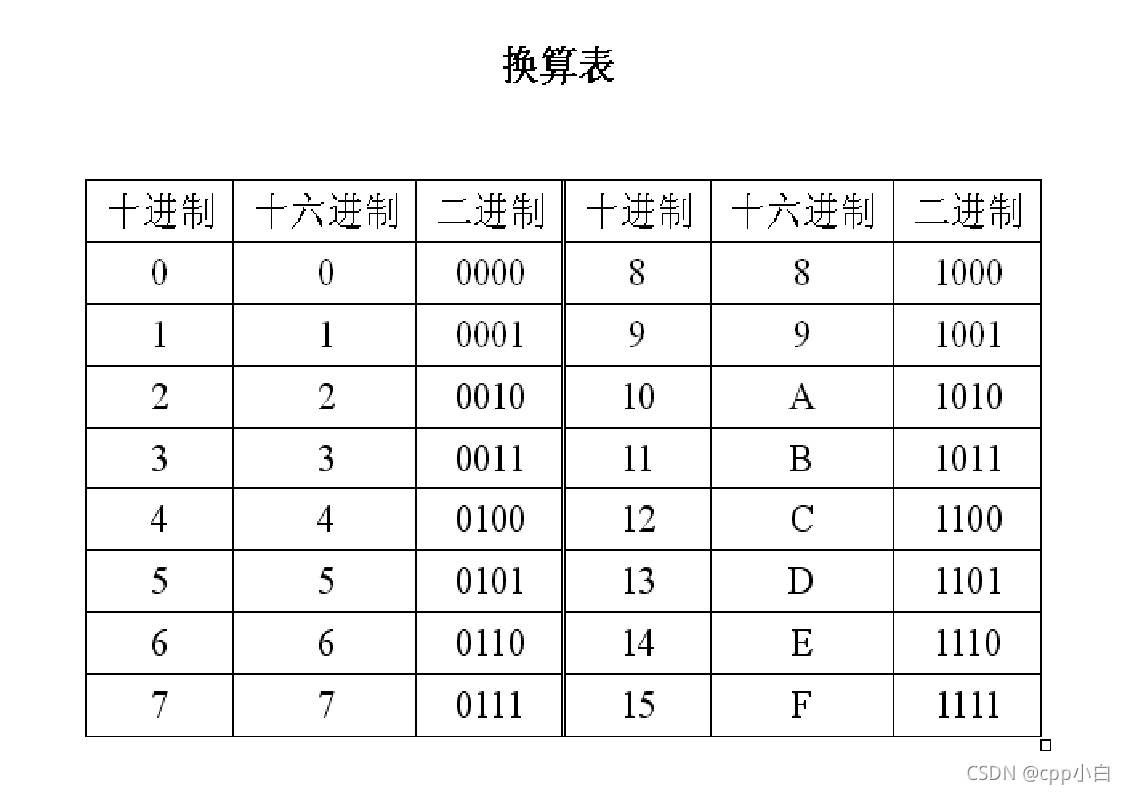
整数的表示形式

这里比较简单，只需要注意各个进制之间的转化即可。

最大公因数与广义欧几里得除法

注意，这里是后方知识的基石，要深刻理解公因数以及欧几里得除法！

最大公因数

定义1.3.1

通过定义可以清楚地了解到最大公因数的意义。当最大公因数为1的时候，我们就可以说这两个数互素。

关于最大公因数，我们有以下几个性质：

广义欧几里得除法与计算最大公因数

如何求解最大公因数，在高中的时候有欧几里得除法，有秦九韶算法。
在这里介绍的是广义欧几里得算法。
由刚刚的定理可以知道余数与商的最大公因数等于被除数与商的最大公因数由此我们可以将两个整数不断分解，最终求出两个整数的最大公约数。

熟练掌握广义欧几里得除法是我们求解最大公因数的基石。

从广义欧几里得除法中不难观察到如果我们将rn不断回带就可以逐次的消去中间量r最终得到最大公因数与两个整数之间的关系。
即贝祖定理

定理1.3.5（贝祖定理）

设a,b是两个正整数，存在整数s,t使得：sa+tb=(a,b)

这意味着整数和最大公因数有着直接的关系。最大公因数可以由两个整数和两个未知数表示，对证明一些结论有很大作用。
并且s，t是可以确定的。

最大公因数的进一步性质：

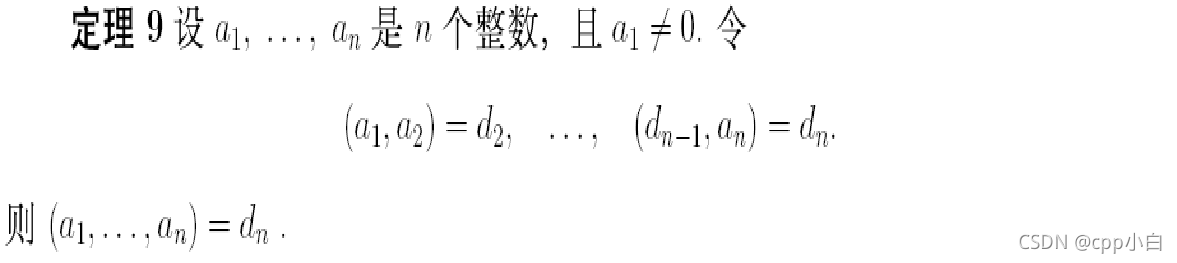
以上定理都可以用贝祖定理证明。

多个整数的最大公因数计算

可以利用广义欧几里得除法，先求出两个数的最大公因数，再将其带入到其他数中验证。

形如 2^a-1 的整数及其最大公因数
设a,b是两个正整数，则2^a-1 被 2^b-1 除的最小非负余数是2^r-1 ,其中r是a被b除的最小非负余数。

引理

设a,b是两个正整数，则2^a-1 被 2^b-1 的最大公因数是2^(a,b)-1

定理1.3.16

设a,b是两个正整数，则2^a-1 被 2^b-1互素的充要条件是a,b互素。

最小公倍数

最小公倍数和最大公因数有一些相同的地方，这里只表明他们的关系：

定理

设a，b是两个正整数，则ab=[a,b](a,b)

素数的算数基本定理

通过算数基本定理，我们可以将任何数分解成素数的幂次方乘积的形式。对后面的计算证明有很大帮助！

至此第一章主要知识点梳理完毕。