汉诺塔Tower of Hanoi_汉若塔怎么挪到制定位置-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_46660172/article/details/107522830

本文详细介绍了汉诺塔问题的背景、解决思路及Java代码实现。通过将问题分解为更小的部分，递归地解决了从A杆将金盘全部移动到C杆的问题，同时保持原有的顺序。文章提供了具体的操作步骤和代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

汉诺塔问题

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标:把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

解决思路

由于64个数量过于庞大，即使是很擅长重复运算的计算器运行64个也要花费几百年的时间，所以我们以四个为例子。
采用整体法看待，将4个盘子划分成两部分，部分一底下最大的那个盘子，部分二是其余盘子。

第一步：将部分二先移动到位置C再移动到位置B
（为什么不直接将部分二移动到位置B呢？
因为咱们是将其余盘子看作整体，方便理解，但实际情况是每次只能够移动一个盘子，所以小的盘子必须先要放到位置C，然后再将比它大一个盘子放到位置B）
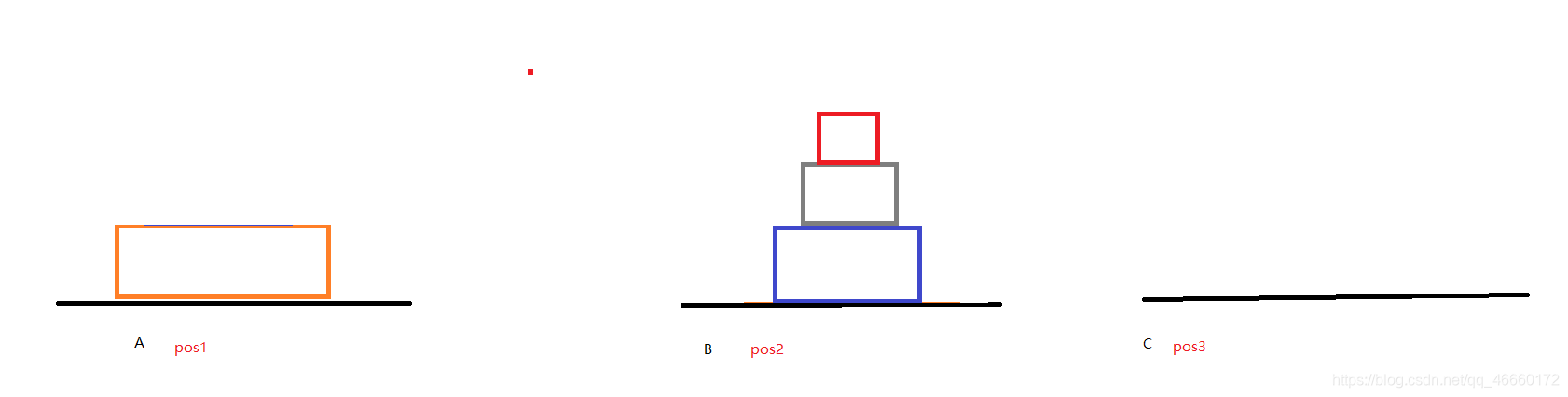
在这里插入图片描述
第二步：将部分二移动到位置C

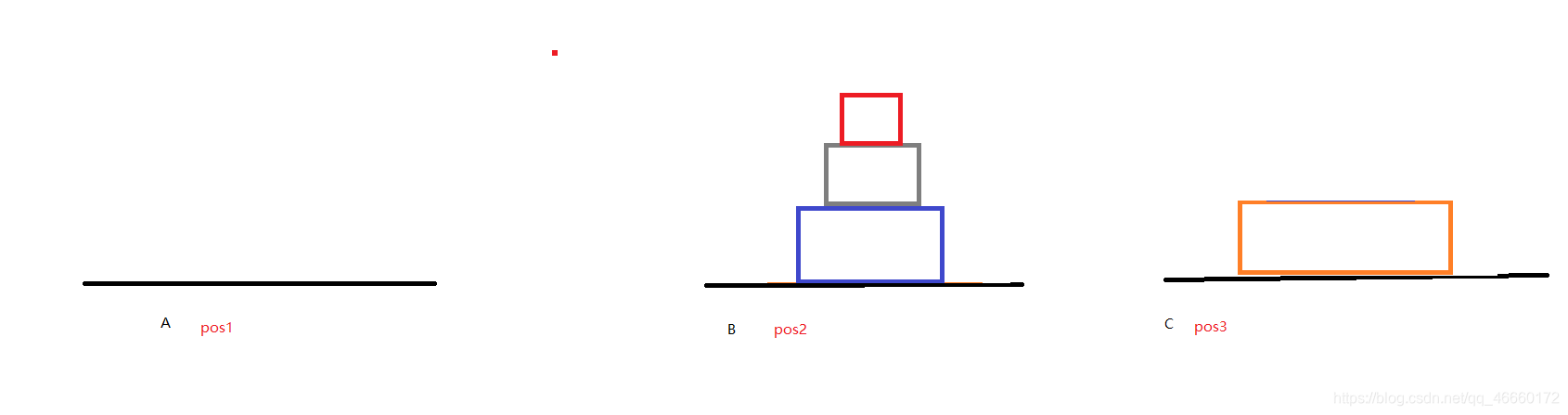
第三步：将部分二先移动到位置C再移动到位置A

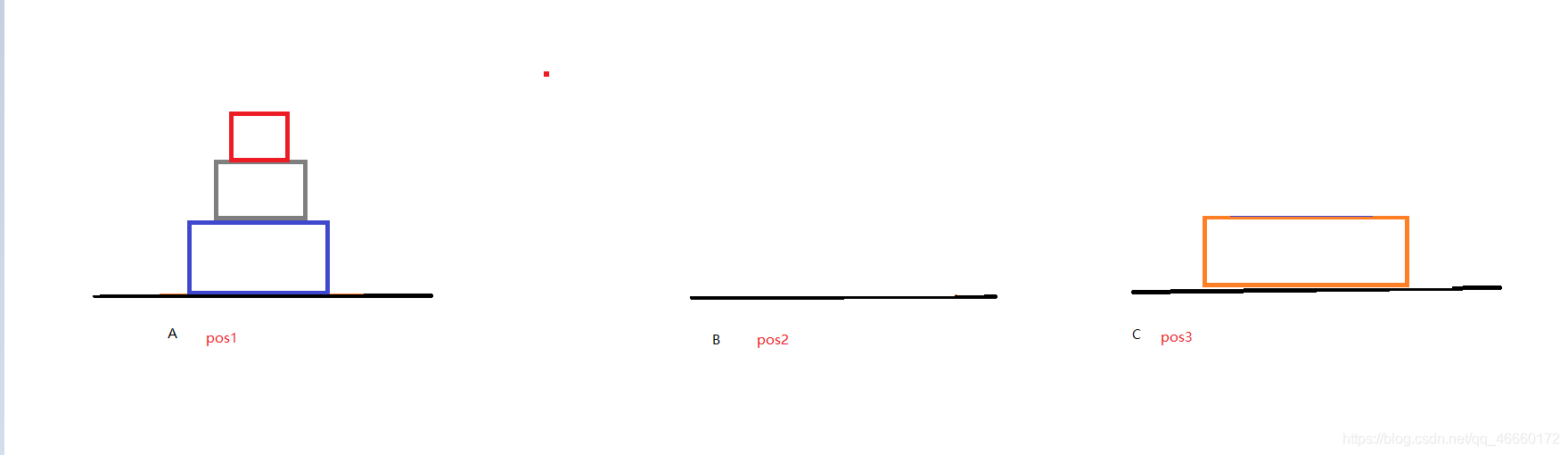
第四步：重复操作。

代码实现


```java

public class towerOfHanoi {
    public static void move(char pos1 , char pos2){         //pos分别表示位置A B C
        System.out.print(pos1 +"->" + pos2+" ");//将A上的盘子移动到C
    }
    public static void hanoi(int n ,char pos1 , char pos2,char pos3){
        if(n == 1){
            move(pos1, pos3);
        }
        else{
            hanoi(n-1,pos1,pos3,pos2);//执行第一步
            move(pos1,pos3);//执行第二步
            hanoi(n-1,pos2,pos3,pos1);//执行第三步

    }
    }

    public static void main(String[] args) {
        hanoi(3,'A','B','C');
    }
}