
开源内容:https://github.com/TommyZihao/zihao_course/tree/main/CS224W
子豪兄B 站视频:https://space.bilibili.com/1900783/channel/collectiondetail?sid=915098
斯坦福官方课程主页:https://web.stanford.edu/class/cs224w
图的基本表示
节点
N
N
N:nodes、vertices
边
E
E
E:links、edges
图
G
(
N
,
E
)
G(N,E)
G(N,E):network、graph
图的本体设计
如何设计本体图Ontology取决于我们将来想解决什么问题
- 本体图的设计可能是唯一的、无歧义(例如社交网络)
- 本体图的设计可能不是唯一的(例如红楼梦包括人物、地点、事件)

图的种类
-
无向图:连接是无方向的
-
有向图:连接是有方向的

-
异质图:节点或连接存在不同的类型

-
二分图(Bipartite Graph):节点只有两类,是一种特殊的异质图


节点连接数

- 无向图
- 节点的度 k i k_i ki:节点连接的边的数量
- 节点的平均度 k ˉ \bar{k} kˉ: k ˉ = ⟨ k ⟩ = 1 N ∑ i = 1 N k i = 2 E N \bar{k}=\langle k\rangle=\frac{1}{N} \sum_{i=1}^{N} k_{i}=\frac{2 E}{N} kˉ=⟨k⟩=N1∑i=1Nki=N2E
- 有向图
- 节点的入度/出度 k i i n / o u t k^{in/out}_{i} kiin/out:指向节点的边的数量/从节点射出的边的数量
- 节点平均度为 k ˉ i n / o u t = E N \bar{k}^{in/out}=\frac{E}{N} kˉin/out=NE
邻接矩阵


连接列表和邻接列表
连接列表:只记录存在连接的节点对

邻接列表:只记录相关连接的节点,每个节点占用一行

其它种类的图
- Unweighted(无权无向图)
- Weighted(带权无向图)
- Self-edges(self-loops)(带自环无向图)
- Multigraph(多通路无向图)


图的连通性
连通图和非连通图

连通图的邻接矩阵是分块对角的形式

有向图的可达性
强连通图:有向图中任意两个顶点可达
弱连通图:有向图的基图任意两个顶点可达

图中存在强连通子图,我们称这些子图为强连通域

传统图机器学习
即人工特征工程+机器学习,将节点、边和图设计为d维向量输入到机器学习算法中进行预测

特征分类
节点、连接、子图和全图都可以有特征,以银行的风控用户为例。
属性特征包括:收入、学历、年龄、婚姻状态、工作单位、征信、个性签名
连接特征包括:交易记录、是否违约等
图特征包括:共同客户、关联公司等
传统机器学习步骤

- 把节点、连接、全图变成D维向量
- 特征工程就是构造新的D维向量
- 将这些D维向量输入到机器学习模型中进行训练
- 给出一个新的图(节点、连接、全图)和特征,进行预测
特征工程
节点层面的特征工程
以节点预测任务为例
- 基本流程:已知 G = ( V , E ) G=(V,E) G=(V,E),通过机器学习算法学习一个方程 f : V ⟶ R f:V \longrightarrow \R f:V⟶R
- 任务:使用已知节点图,预测未知节点的类别
- 构造的节点特征:Node degree(节点的度)、Node centrality(节点重要度)、Clustering coefficient(聚集系数)、Graphlets(子图模式)
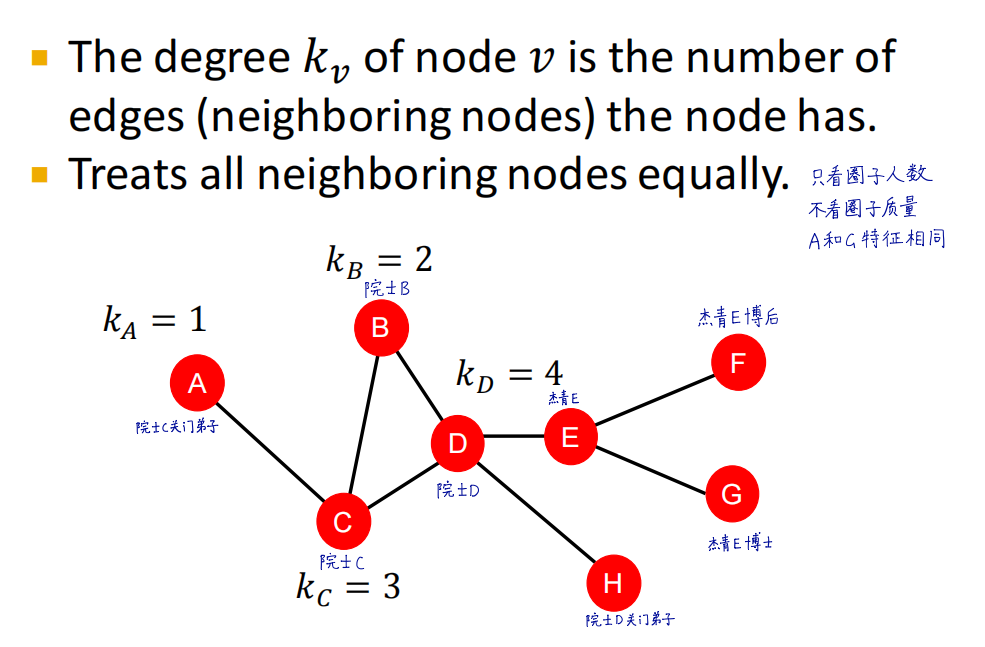
节点的度
A和G的度都是1,但是很明显A的节点重要程度要大于G
节点的重要度
节点的度只考虑了节点连接边的数量,但是忽视了节点的质量。节点的重要度 c v c_v cv考虑了图中节点的重要程度,有以下几种衡量节点重要程度的方式:
- Eigenvector centrality(特征向量中心性):选择
λ
m
a
x
\lambda_{max}
λmax对用的特征向量作为中心性向量,节点数值越大重要性越高


- Betweenness centrality(介数中心性):经过节点的其它任意两节点之间的最短路径条数越多,节点重要性越高

- Closeness centrailty(紧密中心性):节点到其它节点的最短路径之和越短,节点重要性越高

聚集系数(Clustering coefficient)

子图模式(Graphlets)

节点层面Graphlet是从局部(节点)的角度出发来描述节点。 用不同graphlet中的节点相对位置(局部信息),来形成一个节点的向量表示。
2个节点有1种节点角色;3个节点有2种节点角色;4个节点有5种节点角色。2-5个节点共有73种节点角色,标识的节点GDV具有73维向量。

GDV的定义:一个节点所在位置的频率组成的向量。通过计算一个节点所在的Graphlets中不同的非对称位置,可以对节点附近的局部结构进行衡量。
计算方式:选择
n
n
n个节点的Graphlet来标识一个节点的GDV,以下图为例:
这里选择三个节点的graphlets,有四种节点角色
a
、
b
、
c
、
d
a、b、c、d
a、b、c、d,分别数
u
u
u节点周围各种节点角色的数量,将结果组成一个GDV,维度为四维

比较两个节点的GDV向量,计算距离和相似度
连接层面的特征工程
任务:通过已知连接补全未知连接
方案:
- 直接提取link的特征,把link变成D维向量(更推荐使用)
- 把link两端的D维向量拼接在一起
连接预测的场景可以分为以下两种情况:
- 随时间不变的(蛋白质分子):随机删除一些连接,然后再预测这些连接
- 随时间变化的(论文引用、社交网络):使用上一个时间区段的图预测下一个时间区段的L个连接,选出
T
o
p
N
Top N
TopN个连接,将这些连接和下一个真实时刻的连接进行比较,用于评估模型性能
预测的具体步骤:- 提取连接特征,转变为D维向量,计算分数
- 根据分数对连接进行从高到低降序排列
- 预测 T o p N Top N TopN个连接
- 将预测的连接与真实连接进行比较,并评估算法性能
连接特征分类
基于两节点距离(Distance-based feature)
计算两点之间的最短路径,但是没有得到最短路径的条数

基于两节点局部连接信息(Local neighborhood overlap)
捕获两个节点之间公共的邻居节点,但是当没有公共的邻居节点时会失效

基于两节点在全图的连接信息(Global neighborhood overlap)
使用全图的信息信息(Katz系数)对两个节点的连接进行打分
Katz index:节点
u
u
u和节点
v
v
v之间长度为
K
K
K的路径个数之和,其中
K
=
1...
k
K=1...k
K=1...k
计算方法如下:



全图层面的特征工程
目标:提取出的特征
ϕ
(
x
)
\phi(x)
ϕ(x)可以反映全图的结构特点
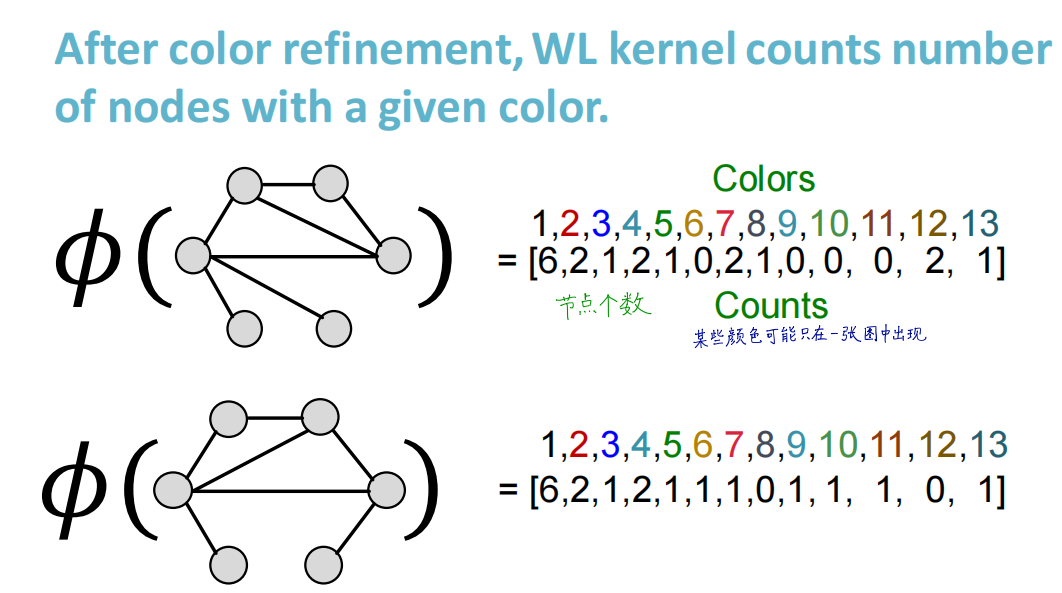
关键思想:将Bag-of-Words(BoW)算法应用在图上,把图看成文章,节点看成单词,这个算法关注了节点,但是无法表示连接结构,例如下图两个图节点相同,连接不同。

当我们使用Bag-of node degrees时,算法只关注了节点的度,忽略了节点和连接结构

我们可以对Bag of *的思想进行推广 ,有了Graphlet Kernel算法和Weisfeiler-Lehman (WL) Kernel算法
边层面的Graphlet
在介绍这两个算法之前,我们先介绍边层面的Graphlet,它和节点层面的Graphlet有一下两点不同:
- 可以存在孤立节点
- 计数全图的Graphlet个数而非特定节点邻域的Graphlet个数


Graphlet Kernel算法


Weisfeiler-Lehman (WL) Kernel算法
- 算法基本介绍

- 算法流程:

- 算法举例:




- 算法时间复杂度:由于每一轮迭代主要处理的是排序,那么假设对于某个图 G G G,每一次迭代可以生成的复合集中有 m m m个元素,根据计数排序,迭代时间复杂度就是 O ( m ) O(m) O(m)。每一轮生成的复合集的元素数量 m m m ≥ \ge ≥结点数 n n n的,因为每个结点的复合集都至少包含自己的标签。
如果迭代次数为h,那么威斯费勒-莱曼算法计算复杂度就是O(hm)

总结
本文介绍图的基本表示包括无向图、有向图、二分图、有权图、邻接矩阵,同时对图的连通性进行了介绍。
本文还介绍了传统的图机器学习,传统的图机器学习的关键在于特征工程,图的特征工程主要包括节点、连接和全图三个层面。
- 节点层面的特征工程:Node degree(节点的度)、Eigenvector centrality(特征向量中心性),Betweenness centrality(介数中心性)、loseness centrailty(紧密中心性)、Clustering coefficient(聚集系数)、Graphlets(子图模式)
- 连接层面的特征工程:基于两节点距离(Distance-based feature)、基于两节点局部连接信息(Local neighborhood overlap)、基于两节点在全图的连接信息(Global neighborhood overlap)
- 全图层面的特征工程:Graphlet Kernel算法和Weisfeiler-Lehman Kernel算法都是通过Bag of *的思想泛化而来的,后者的计算效率更高,而且和GNN的思想很接近。










 文章详细介绍了图的基本概念,如无向图、有向图、节点度和邻接矩阵,以及图的连通性。在机器学习的上下文中,重点讨论了特征工程在节点、连接和全图层面的应用,包括节点的度、重要度、聚集系数、子图模式,以及连接层面的特征如距离和局部连接信息。此外,还提到了全图层面的GraphletKernel和Weisfeiler-LehmanKernel算法。
文章详细介绍了图的基本概念,如无向图、有向图、节点度和邻接矩阵,以及图的连通性。在机器学习的上下文中,重点讨论了特征工程在节点、连接和全图层面的应用,包括节点的度、重要度、聚集系数、子图模式,以及连接层面的特征如距离和局部连接信息。此外,还提到了全图层面的GraphletKernel和Weisfeiler-LehmanKernel算法。

















 1348
1348

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










