多维随机变量及其分布
二维随机变量及其分布
二维随机变量定义
X,Y均为一维随机变量，则(X,Y)称为二维随机变量。
分布函数
F ( x , y ) = P ( X ≤ x , Y ≤ y ) , − ∞ < x < + ∞ , − ∞ < y < + ∞ F(x,y)=P(X\le x,Y\le y),-\infin<x<+\infin,-\infin<y<+\infin F(x,y)=P(X≤x,Y≤y),−∞<x<+∞,−∞<y<+∞
分布函数的性质
二维随机变量的边缘分布
二维随机变量的条件分布
二维离散型随机变量
如果随机变量(X,Y)可能取值为有限个或可数无穷个 ( x i , y i ) , i , j = 1 , 2 , . . . , (x_i,y_i),i,j=1,2,..., (xi,yi),i,j=1,2,...,，则称为二维离散型随机变量。
概率分布
性质
边缘概率分布
条件概率分布
二维连续型随机变量
概率密度函数的性质
边缘密度
条件概率
随机变量的独立性
二维均匀分布和二维正态分布
二维均匀分布
二维正态分布
性质：
（1）
X
∼
N
(
μ
1
,
σ
1
2
)
,
Y
∼
N
(
μ
2
,
σ
2
2
)
X\thicksim N(\mu_1,\sigma_1^2),Y\thicksim N(\mu_2,\sigma_2^2)
X∼N(μ1,σ12),Y∼N(μ2,σ22)
（2）X与Y相互独立的充分必要条件是
ρ
=
0.
\rho=0.
ρ=0.
随机变量函数的分布
X,Y均为离散型随机变量
Z=(X,Y)的分布律球阀与以为离散型类似。
X,Y均为连续型随机变量
公式法
分布函数法
具体步骤：
最值函数
X离散，Y连续
特殊情况——可加性分布
X,Y独立
则：
扫一扫
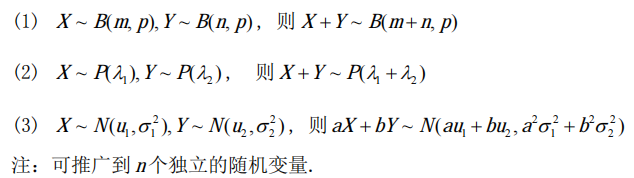
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
