随机变量及其概率分布
随机变量及其分布函数
随机变量
在样本空间 Ω \varOmega Ω上的实值函数 X = X ( ω ) , ω ∈ Ω X=X(\omega),\omega\in\varOmega X=X(ω),ω∈Ω,称 X ( ω ) X(\omega) X(ω)为随机变量，简记 X X X。
分布函数
F ( x ) = P ( X ≤ x ) F(x)=P(X\le x) F(x)=P(X≤x)即F(x)的值为 X 在(−∞, x]内取值的概率.
分布函数的性质
概率计算
F
(
x
−
0
)
=
P
(
X
<
x
)
F(x-0)=P(X<x)
F(x−0)=P(X<x)
离散型随机变量和连续型随机变量
离散型随机变量
定义
X可能取值是有限多个或可数无穷多个。
概率分布
分布律性质
连续型随机变量
定义
如果对随机变量 X X X的分布函数 F ( x ) F(x) F(x)，存在一个非负可积的函数 f ( x ) f(x) f(x)，使得对任意实数 x x x，都有
F
(
x
)
=
∫
−
∞
x
f
(
t
)
d
t
,
−
∞
<
x
<
+
∞
F(x)=\int_{-\infin}^xf(t)dt,-\infin<x<+\infin
F(x)=∫−∞xf(t)dt,−∞<x<+∞
称
X
X
X为连续型随机变量，函数
f
(
x
)
f(x)
f(x)称为
X
X
X的概率密度。
概率密度的性质
常用分布
离散型随机变量
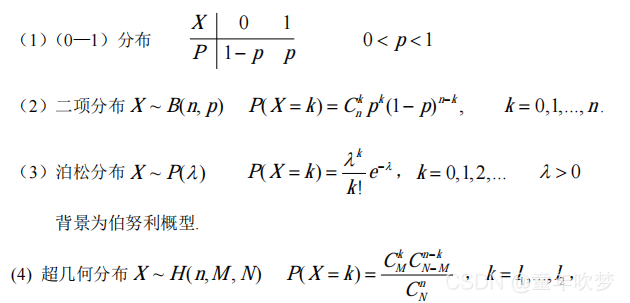
泊松定理
在伯努利试验中，
p
n
p_n
pn代表事件A在实验中出现的概率，它与实验总数n有关，如果
lim
n
→
+
∞
n
p
n
=
λ
\lim\limits_{n\to{+\infin}}np_n=\lambda
n→+∞limnpn=λ,则
lim
n
→
+
∞
C
n
k
p
n
k
(
1
−
p
n
)
n
−
k
=
λ
k
k
!
e
−
λ
\lim\limits_{n\to{+\infin}}C_n^kp_n^k(1-p_n)^{n-k}={\lambda^k \over {k!}}e^{-\lambda}
n→+∞limCnkpnk(1−pn)n−k=k!λke−λ
应用泊松定理的要求：
n较大，p较小，np不太大。
连续型随机变量（均匀、指数）
正态分布
随机变量函数的分布
离散型
P
(
X
=
x
k
)
=
p
k
,
k
=
1
,
2
,
.
.
.
P(X=x_k)=p_k,k=1,2,...
P(X=xk)=pk,k=1,2,...
连续型
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
