事件
基本概念

(1)由一个样本点组成的子集是最简单时间,称为基本事件。
(2)每次实验必有
Ω
\varOmega
Ω中某一基本事件(样本点)发生,也就是每次实验
Ω
\varOmega
Ω必然发生,称
Ω
\varOmega
Ω为必然事件。
(3)把不包含任何样本点的空集
∅
\varnothing
∅看成一个事件,每次实验
∅
\varnothing
∅必然不发生,称
∅
\varnothing
∅为不可能事件。
事件的关系

事件的运算律
( ∪ = + , ∩ = ∙ \cup=+,\cap=\bullet ∪=+,∩=∙)
- 交换律: A ∪ B = B ∪ A , A ∩ B = B ∩ A A\cup B=B\cup A,A\cap B=B\cap A A∪B=B∪A,A∩B=B∩A
- 结合律: A ∪ ( B ∪ C ) = ( A ∪ B ) ∪ C , A ∩ ( B ∩ C ) = ( A ∩ B ) ∩ C A\cup (B\cup C)=(A\cup B)\cup C,A\cap (B\cap C)=(A\cap B)\cap C A∪(B∪C)=(A∪B)∪C,A∩(B∩C)=(A∩B)∩C
- 分配律: A ( B + C ) = A B + A C A(B+C)=AB+AC A(B+C)=AB+AC
- 对偶律: A + B ‾ = A ‾ ∙ B ‾ \overline{A+B}=\overline{A}\bullet\overline{B} A+B=A∙B, A ∙ B ‾ = A ‾ + B ‾ \overline{A\bullet B}=\overline{A}+\overline{B} A∙B=A+B
概率、条件概率、独立性
概率的定义
满足三个条件:
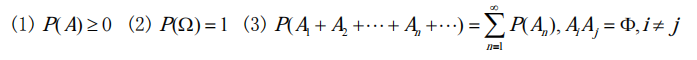
概率的性质
条件概率

乘法公式

全概率公式
知因索果
贝叶斯公式
执果索因

事件的独立性

古典概型与伯努利概型
古典概型

几何概型

伯努利概型









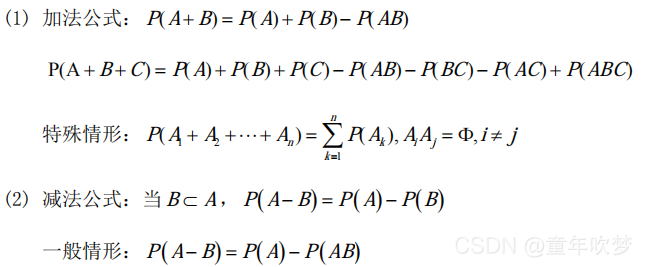



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








