GBDT-2

最新推荐文章于 2023-01-10 12:58:49 发布
原创 最新推荐文章于 2023-01-10 12:58:49 发布 · 242 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

该博客深入探讨了GBDT（梯度提升决策树）中的CART树构造过程，包括在回归和分类问题中的应用。对于回归问题，GBDT通过拟合残差来构建树；而在分类问题中，利用Softmax处理概率映射，迭代拟合概率差值。内容涉及特征选择、损失函数最小化和树的构建策略，并阐述了预测阶段的实现。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

多分类实例

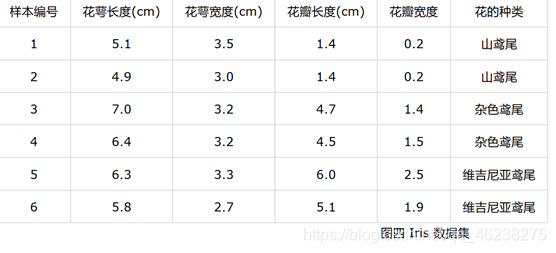
在这里插入图片描述
[1,0,0] 表示样本属于山鸢尾，[0,1,0] 表示样本属于杂色鸢尾，[0,0,1] 表示属于维吉尼亚鸢尾。
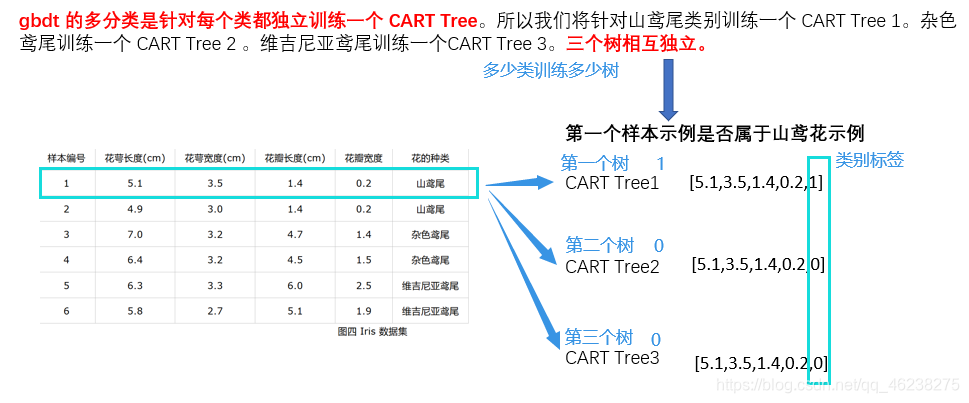
在这里插入图片描述
Cart Tree1生成过程
遍历所有样本对应的所有特征，找其最好的切分条件给其分成树
考虑问题：
1.是哪个特征最合适? 2.是这个特征的什么特征值作为切分点?
举例：
构建第一棵树时，首先遍历到花萼长度，遍历到5.1，假如以5.1作为切分点，小于5.1为一类，大于等于5.1为一类
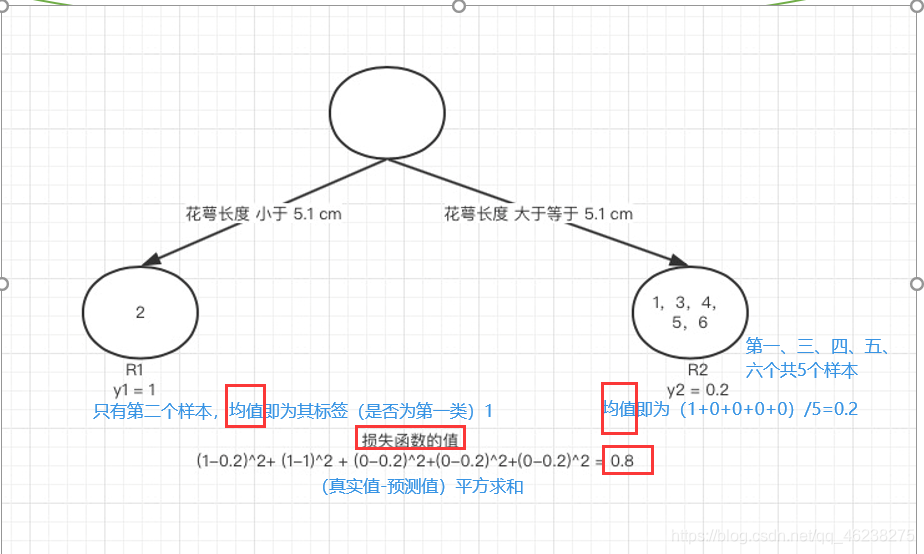在这里插入图片描述y1 为 R1 所有样本的label 的均值 1/1=1。y2 为 R2 所有样本的label 的均值(1+0+0+0+0)/5=0.2

随后，遍历到花萼长度特征的第二个样本的值4.9
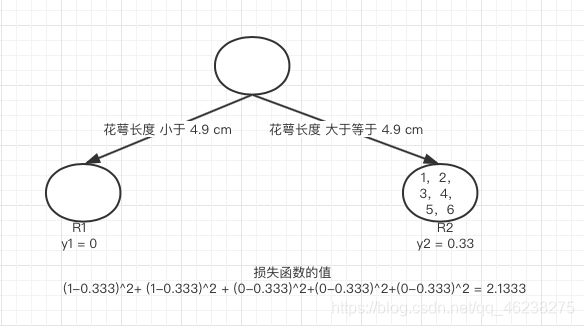
在这里插入图片描述
显然，以4.9切分，其损失值大于特征一的第一个特征值的损失值-舍弃；之后依次遍历，找出最小的损失值对应的切分方式来构建cart tree1,cart tree2、cart tree3 类同
Cart Tree的预测函数
GBDT累加时累加的是f(x)，因此需要对每个树进行表达f(x) 举例
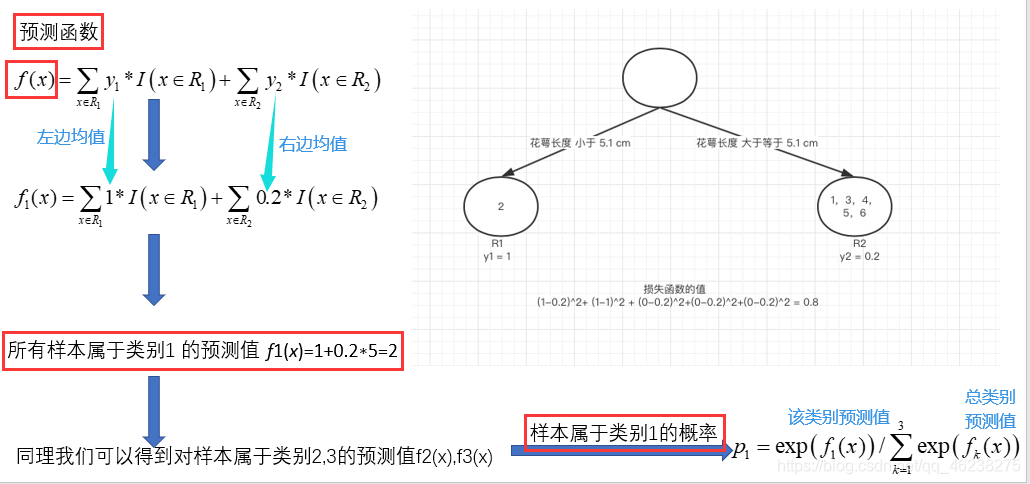
在这里插入图片描述
有了类别概率后即可进行迭代
在这里插入图片描述

GBDT用于回归时使用CART回归树，每次对残差（负梯度）进行拟合。而分类问题要怎么每次对残差拟合？
分类问题：类别相减没有意义。因此，可以用Softmax进行概率的映射，然后每轮拟合概率的残差，不断迭代。
如实际是A类，但构建树预测其是A类的概率为0.8，故下次要拟合概率差值0.2

回归案例

数据
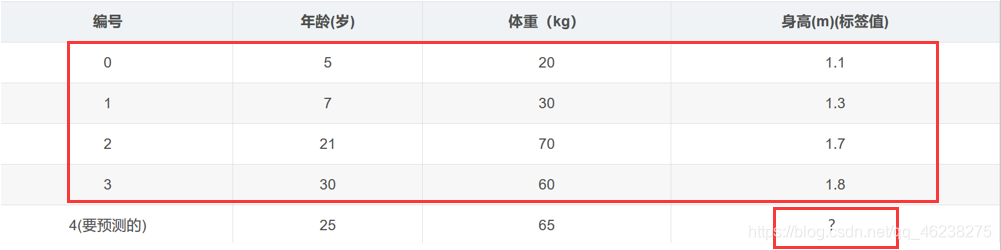
在这里插入图片描述
训练
在这里插入图片描述
1.初始化弱学习器
在这里插入图片描述
2.迭代轮数m=1,2…，M n_trees=5 所以M=5
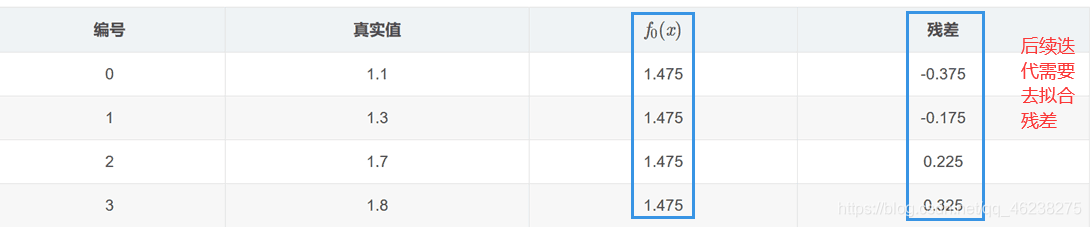
在这里插入图片描述
在这里插入图片描述
将残差作为样本的标签值来训练弱学习器f1(x)
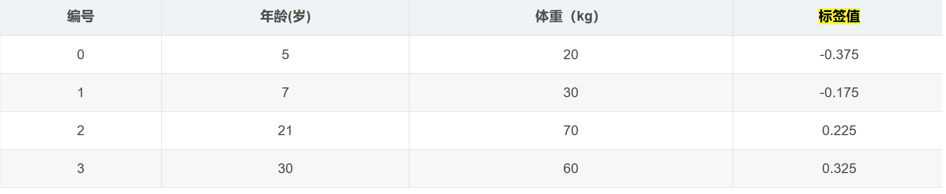
在这里插入图片描述
寻找回归树的最佳划分节点，遍历每个特征的每个可能取值,从年龄特征的5开始，到体重特征的70结束，分别计算分裂后两组数据的平方损失。
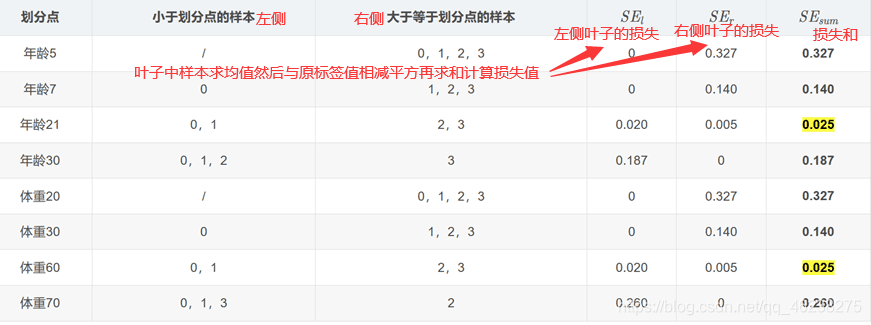
在这里插入图片描述
寻找总平方损失最小为0.025有两个划分点：年龄21和体重60，所以随机选一个作为划分点
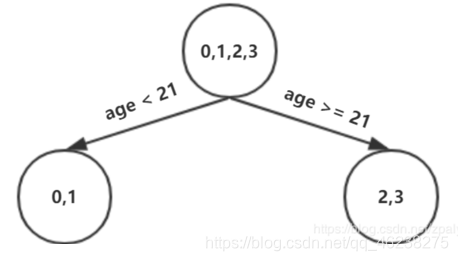
在这里插入图片描述
设置的参数中树的深度max_depth=3，现在树的深度只有2，需要再进行一次划分。这次划分要对左右两个节点分别进行划分：
即重复上述过程，对左节点中样本0，1继续划分；对右节点中样本2，3继续划分
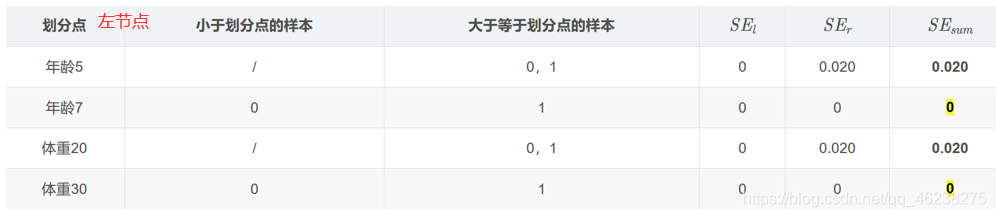
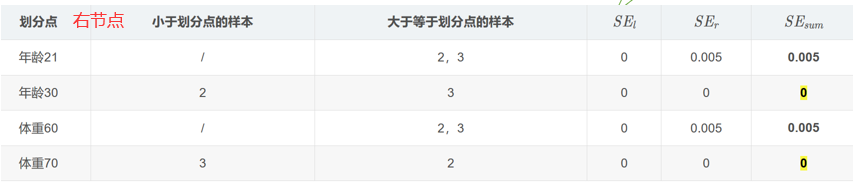
在这里插入图片描述
在这里插入图片描述
从而构造第一棵树
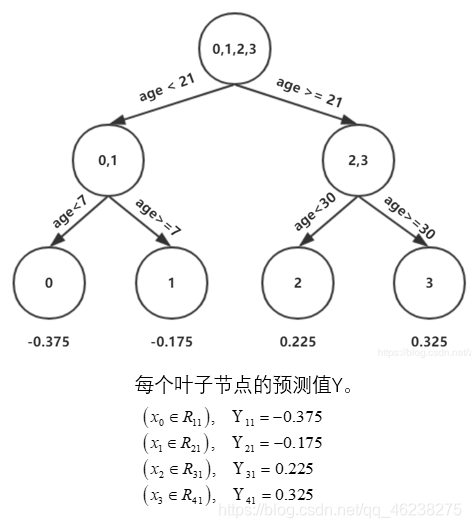
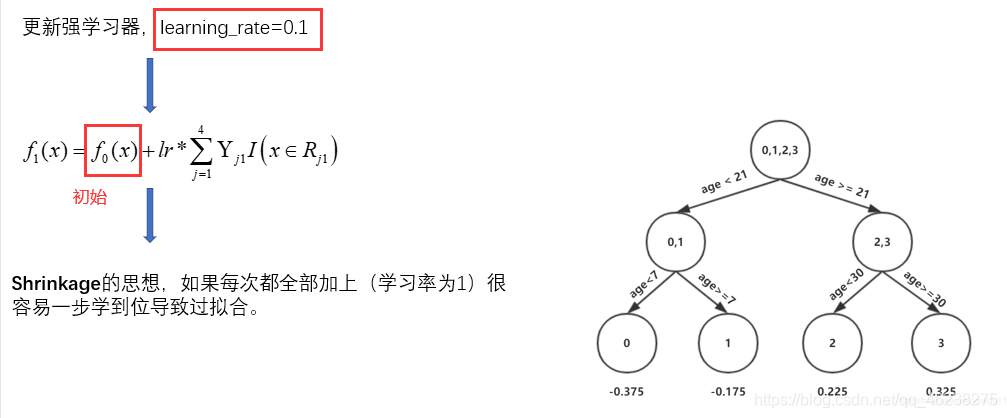
在这里插入图片描述
在这里插入图片描述
设置学习率-防止过拟合
迭代建树
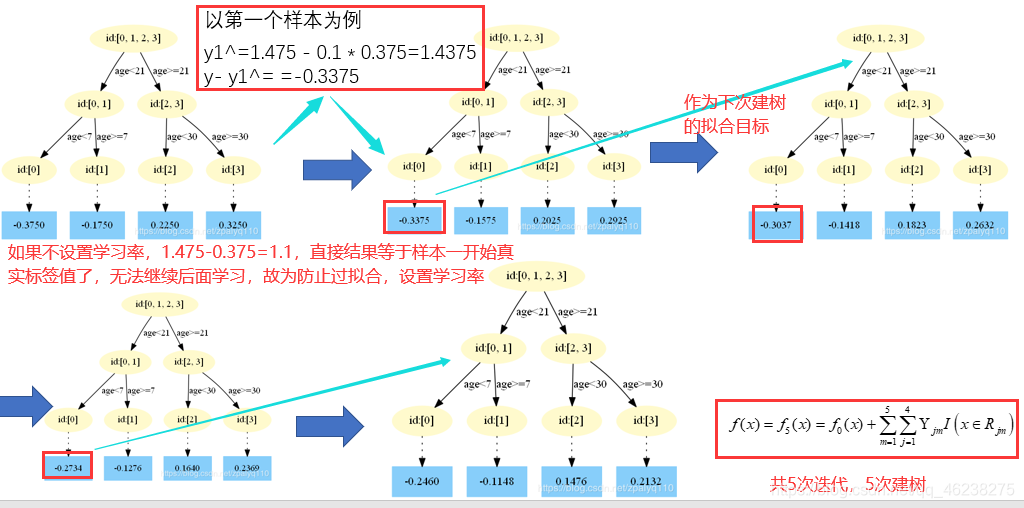
在这里插入图片描述
预测阶段
在这里插入图片描述
利用上面样本建立好的树来进行预测
在这里插入图片描述

算法梳理2：GBDT
harperyeung的博客
01-07 695
目录 1. GBDT概述 2. 前向分步算法 3. 负梯度拟合 5. 回归 6. 二分类，多分类 7. 正则化 8. 优缺点 9. sklearn参数 10. 应用场景 梯度提升树(Gradient Boosting Decison Tree, 以下简称GBDT)，又称GBT（Gradient Boosting Tree）, GTB（Gradient Tree Boosting ），GBRT（G...
GBDT之二分类算法
blinkyou001的博客
01-22 1995
GBDT，全称Gradient Boosting Decision Tree，梯度提升决策树。该算法于1999年由Friedman最早提出。GBDT算法的基本思路是通过对负梯度的不断拟合，实现学习器的更新，得到最终的强学习器。GBDT算法支持回归算法和分类算法，其分类算法支持二分类和多分类。本文介绍其中的二分类算法。对于二分类算法，得到最终的强学习器后，将其转化为正样本事件发生的概率。
GBDT
weixin_43555099的博客
10-10 289
决策树 决策树是一种自上而下，对样本数据进行树形分类的过程，由结点和有向边组成。结点分为内部结点和叶结点，其中每个内部结点表示一个特征或属性。叶节点表示类别。从顶部根节点开始，所有样本聚在一起，经过根节点的划分，样本被划分到不同的子结点中，再根据子结点的特征进一步划分，直至所有样本都被归到某一个类别中。 它是一种监督学习模型，常被用于分类问题和回归问题。 决策树+集成学习------->随机...
GBDT提升树
weixin_46556352的博客
04-05 942
1. 提升树¶ 梯度提升树（Grandient Boosting）是提升树（Boosting Tree）的一种改进算法，所以在讲梯度提升树之前先来说一下提升树。 先来个通俗理解：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。 上面提到的残差是什么呢？ 假设:
随机森林
weiwei19890308的博客
10-01 895
随机森林 随机森林与集成学习的关系： 说到随机森林，就不得不提一下机器学习中的集成学习方法 .随机性： 随机体现在两个方面，生成单颗决策树时，需要进行样本的有放回抽样（自助采样法）， 在生成单颗决策树时，每个结点处，进行特征的随机抽样。 .out-of-bag估计: 每颗决策树的生成都需要自助采样，这时就会有1/3的数据未被选中，这部分数据称为袋外数据。 可以根据这部分数据进行 森林泛...
GBDT-master_机器学习_
09-29
在这个"GBDT-master"项目中，重点是利用GBDT进行机器学习的预测和分类任务，特别是二分类问题。 GBDT的基本原理： 1. **梯度提升**：GBDT的核心思想是通过梯度下降法逐步减小训练数据的损失函数。每次迭代，GBDT...
H-GBDT-master 使用文档1
08-08
**H-GBDT 使用文档1** H-GBDT（可能是基于梯度提升决策树的算法实现）的使用...以上是关于H-GBDT-master的使用文档的主要内容，涵盖了Python环境搭建、依赖库安装以及测试流程，帮助用户顺利地运行和测试H-GBDT算法。
【时间序列预测】MATLAB实现基于GBDT-LSTM梯度提升树（GBDT）结合长短期记忆网络（LSTM）进行时间序列预测的详细项目实例（含完整的程序，GUI设计和代码详解）
最新发布
06-21
内容概要：本文详细介绍了基于GBDT-LSTM梯度提升树（GBDT）结合长短期记忆网络（LSTM）进行时间序列预测的项目实例，涵盖了从项目背景、目标与意义、挑战及解决方案、模型架构、代码实现到部署与应用的全流程。...
基于三维荧光光谱和GBDT-LR的褐潮藻辨识.docx
02-23
本文提出的“基于三维荧光光谱和GBDT-LR的褐潮藻辨识”方法，旨在提高识别的准确性和效率。以下是该研究的关键知识点： 1. **三维荧光光谱技术**：这是一种非破坏性的分析方法，能够获取样本的详细光谱信息。在海洋...
使用GBDT算法对新闻数据集进行多分类任务_GBDT-20news-bydate.zip
10-01
GBDT（Gradient Boosting Decision Tree）是一种利用梯度提升技术的决策树算法，它是一种集成学习方法，通过在每一轮中增加新的弱分类器来改进模型性能，每个分类器都会针对前一个分类器的残差进行学习。在处理多...
GBDT算法
PanDawson的博客
03-19 4486
GBDT算法 Gradient Boosting Decision Tree 以梯度为优化目标，以提升为手段（前面讲到的集成算法中的串联），基础模型为决策树（这里用的是回归树）的算法 GBDT简单来说，就是用多个树串联，提升模型的效果 以下是学习唐宇迪老师的GBDT算法的理解，文末有其他直接更详细的的关于GBDT算法的实现 回归树的形式是CART 即二叉树 使用回归树做分类和回归都...
【基础算法】 GBDT/XGBoost 常见问题
fengdu78的博客
04-20 2385
原文作者：Jack Stack原文：https://zhuanlan.zhihu.com/p/81368182在非深度学习的机器学习模型中，基于GBDT算法的XGBoost、lightg...
GBDT算法梳理
xiu351084315的博客
04-07 1545
1、GBDT基础概念与理解分析 GBDT(Gradient Boosting Decision Tree)又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力（generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模...
机器学习-随机森林（Random Forest）
happy game
02-18 1572
一、回归树的缺点 1、回归树算法的方差大 2、一种降低方差的方式是平均多个模型的预测：Bagging（Bootstrap Aggregating） 3、随机森林：Bagging多棵树 二、Bootstrap Aggregating 通过对原始数据D= {x1,x2,x3,...,xn}进行n次有放回采样n个数据集D，得到Bootstrap样本。（对原始数据进行有放回随机采样，抽取数量等于原始数据样本数，可能出现重复数据） 例：原始样本为：D{x1,x2,x3} 则bootstrap可能为：D.
机器学习算法（十五）：GBDT
weixin_39910711的博客
02-15 8561
关于树的几个ensemble模型的比较（GBDT、xgBoost、lightGBM、RF）： https://blog.youkuaiyun.com/xwd18280820053/article/details/68927422 1 决策树 决策树详见：https://blog.youkuaiyun.com/weixin_39910711/article/details/79468798 ...
机器学习笔记
提子同学是我
01-10 2671
机器学习笔记
机器学习之集成学习算法
黑马程序员官方博客
12-30 1199
集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生。
（六）如何利用Python从头开始实现随机森林算法
CoderPai的博客
07-19 3341
作者：chen_h 微信号 & QQ：862251340 微信公众号：coderpai （一）机器学习中的集成学习入门 （二）bagging 方法 （三）使用Python进行交易的随机森林算法 （四）Python中随机森林的实现与解释 （五）如何用 Python 从头开始实现 Bagging 算法 （六）如何利用Python从头开始实现随机森林算法 介绍 随机森林是集成学习中一个主要...
从零开始构建随机森林并了解真实数据产品
weixin_41697507的博客
04-27 792
Introduction 作为数据科学家和机器学习从业者，我们遇到并学习了大量的算法。 你有没有想过每个算法的真正用处在哪里？ 大多数机器学习技术的主要目的是扩展黑客马拉松的排行榜吗？ 不必要。 检查和了解机器学习在现实世界的行业场景中的使用位置和方式非常重要。 这就是我们大多数人正在工作的地方（或最终会工作）。 这就是我打算在我们流行系列的第3部分中展示的内容，其中包括fast.ai机器学习课程...
GBDT-MO
03-25
### GBDT多目标优化（GBDT-MO）的解释与实现 Gradient Boosting Decision Trees (GBDT) 是一种强大的机器学习算法，广泛应用于回归和分类任务。当扩展到多目标场景时，即 Gradient Boosting Decision Tree Multi-Objective (GBDT-MO)，其核心思想在于通过集成多个弱学习器来逼近复杂的多维目标函数。 #### 多目标优化背景 在传统的单目标优化中，模型的目标是最小化单一损失函数。然而，在实际应用中，许多问题涉及多个相互冲突或互补的目标。例如，在金融领域可能需要同时最大化收益并最小化风险；或者在工程设计中平衡性能、成本和可靠性等多个指标[^1]。 为了应对这些挑战，GBDT-MO 将标准 GBDT 的框架推广至能够处理多个目标的情况。具体来说，它试图找到一组 Pareto 最优解，使得任何进一步改进某个目标都会导致其他目标变差。 #### 实现细节 以下是构建 GBDT-MO 的几个关键技术要点： 1. **目标定义** 需要明确定义所有待优化的目标及其对应的度量方式。对于 k 个目标 \( f_1(x), f_2(x), ..., f_k(x) \)，可以采用加权求和法或将它们转化为约束条件的形式。 2. **树结构更新机制** 在每一轮迭代过程中，基于当前残差计算新的决策树，并将其加入现有模型集合中。针对多目标情况下的残差估计方法有多种选择，比如利用梯度向量的方向信息作为指导信号[^2]。 3. **分裂准则调整** 原始 GBDT 使用的是单一目标导向的信息增益衡量节点划分质量。而在 MO 版本里，则需考虑综合各个子目标的表现差异来进行更合理的切分操作。 下面给出一段 Python 示例代码展示如何自定义一个多目标版本的 XGBoost 或 LightGBM 训练流程： ```python import numpy as np from sklearn.datasets import make_regression from lightgbm import LGBMRegressor def multi_objective_loss(y_true, y_pred): """Custom loss function combining multiple objectives.""" residuals = [] for i in range(len(objectives)): residual_i = objectives[i](y_true[:,i], y_pred[:,i]) residuals.append(residual_i) combined_residual = sum([w*r for w,r in zip(weights,residuals)]) grad = -np.sign(combined_residual) hess = np.ones_like(grad) return grad.flatten(), hess.flatten() # Example usage with synthetic data X, Y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42) objectives = [lambda yt, yp: abs(yp-yt)**2, lambda yt, yp: max((yt-yp)/abs(t),0)] # Define your own objective functions here. weights=[0.7, 0.3] model = LGBMRegressor(boosting_type='gbdt', num_leaves=31, learning_rate=0.05, n_estimators=100, reg_alpha=0., reg_lambda=0.) model.set_params(**{'objective':multi_objective_loss}) model.fit(X,Y.reshape(-1,len(objectives))) ``` 上述代码片段展示了如何定制适合特定应用场景的需求组合而成的新颖评价体系，并据此训练得到满足预期效果的最佳参数配置方案。 #### 总结 通过对传统 GBDT 方法稍作修改即可轻松支持多目标情形下复杂关系建模需求。这种方法不仅保留了原有技术优势特性——诸如高效性、鲁棒性和灵活性等优点外，还额外增加了适应多样化业务诉求的能力。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值