同余问题-快速幂

同余问题

---

一：同余

A: 概念

​ 给定整数m，整数a,b，若a%m=b%m,称a,b对m同余，记作 a$\equiv$b(mod m)

重要定理：

1: 对称性a$\equiv$b(mod m) => b$\equiv$a(mod m) 自反性a$\equiv$a(mod m) 传递性a$\equiv$b(mod m),b$\equiv$c(mod m) =>a$\equiv$c(mod m)

2: a$\equiv$b(mod m) 且 c $\equiv$ d(mod m) 则ax+cy $\equiv$ bx+dy (mod m) x,y为任意整数； ac $\equiv$ bd (mod m); $a^n$ $\equiv$ $b^n$(mod m)

3：a $\equiv$ b (mod m) 则(a,m)=(b,m)

4: 若 ac $\equiv$ bc (mod m),且(c,m)=d,则a$\equiv$b(mod m/d)

B:应用

Fibonacci Again(hdu 1021)
Problem Description：
There are another kind of Fibonacci numbers: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2).

Input：
Input consists of a sequence of lines, each containing an integer n. (n < 1,000,000).

Output：
Print the word “yes” if 3 divide evenly into F(n).
Print the word “no” if not.

由同余基本性质有 F(n) $\equiv$ (F(n-1)+F(n-2))(mod 3) , 根据前两项算出当前项F(n)对3取余的结果

#include <cstdio>
using namespace std;
const int MAXN=1000005;
int f[MAXN];
int main()
{
    f[0]=7%3;
    f[1]=11%3;
    for(int i=2;i<1000000;i++)
        f[i]=(f[i-1]%3+f[i-2]%3)%3;
        
    int n;
    while(scanf("%d",&n)!=EOF){
        if(f[n]==0) printf("yes\n");
        else printf("no\n");
    }
    return 0;
}

同理，对于 $a^b$%m

同余性质有 ab $\equiv$ (a%m)(b%m)(mod m)

二：线性同余方程

​ a,b是整数，m是正整数，形如 ax $\equiv$ b(mod m),且x是未知整数的同余式是一元线性同余方程

求解：
由同余方程可得 ax + my =b (y为整数), 这个方程称为二元一次不定方程

​ 设 d=(a,m) ,如果不满足d|b，则方程无解
反之，*a = $a_0$*d ; m = $m_0$*d; 则 $a_0$x + $m_0$y = b/d
​ 此时($a_0$,$m_0$) = 1,利用扩展欧几里得算法得出方程的解x，虽然x不唯一但是同属于一个模m剩余系。

---

扩展欧几里得算法是求 ax+by=c；

其中c%gcd(a,b)==0;不满足就无解

一般的，我们都让这些常量互质，即让a,b,c都除以gcd(a,b);

这时，我们可以得出两个方程：

ax+by=1;

bx1+a%by1=1;

之所以等于1是因为好求，并且最后得出x乘c就好了。

采用第二个式子的原因是，如果一直迭代下去，就会得到一个值，y的系数为1；

此时令当前方程的x=1,y=1-a(当前的a)再递归回去就能解出最开始的x

方法大致是这样的

令 x=y1;

解出当前y与x1之间的关系 然后就一步一步迭代，直到y的系数为1时，再回溯回来就是解了；

当然解不是唯一的 x的解系为x + b/gcd(a,b)*k k为整数。

模板：

void _gcd(long long a,long long b,long long &x,long long &y){
    if(b==1){
        x=1;
        y=1-a;
        return;
    }
    else{
        long long x1,y1;
        _gcd(b,a%b,x1,y1);
        x=y1;
        y=x1-(a/b)*y1;
    }
}

解一元线性同余方程组

​ 任何一个一元同余方程都可变成若干个形如 x $\equiv$ b(mod m) 的方程

​ 对于模线性方程组，可以进行方程组合并，求出合并后方程的解，就可以很快推出方程的最终解。

​ x $\equiv$ $b_1$(mod $m_1$)

​ x $\equiv$ $b_2$(mod $m_2$)

令 m =[$m_1$ , $m_2$] , 此方程组有解的充要条件是($m_1$ , $m_2$) | ($b_1$ - $b_2$) , 此时方程仅有一个小于m的非负整数解

=> x = $b_1$ + $m_1$$y_1$

​ x = $b_2$ + $m_2$$y_2$**

=> $b_1$ + $m_1$$y_1$ = $b_2$ + $m_2$$y_2$

=> $m_1$$y_1$ - $m_2$$y_2$ = $b_2$ - $b_1$ 利用欧几里得算法求出$y_1$,代入方程组得小于m的非负整数解解为 x = ($b_1$ + $m_1$$y_1$)%m

合并：

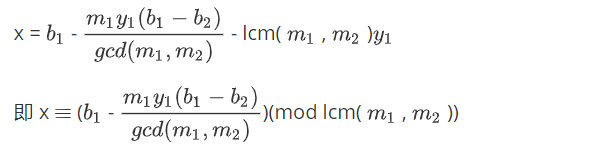
因此不管方程有多少个，都可以两两合并解决，求得最终解

Hello Kiki (hdu 3579)

Description
Hello Kiki is such a lovely girl that she loves doing counting in a different way. For example, when she is counting X coins, she count them N times. Each time she divide the coins into several same sized groups and write down the group size Mi and the number of the remaining coins Ai on her note.
One day Kiki’s father found her note and he wanted to know how much coins Kiki was counting.
Input
The first line is T indicating the number of test cases.
Each case contains N on the first line, Mi(1 <= i <= N) on the second line, and corresponding(相当的) Ai(1 <= i <= N) on the third line.
All numbers in the input and output are integers.
1 <= T <= 100, 1 <= N <= 6, 1 <= Mi <= 50, 0 <= Ai < Mi
Output
For each case output the least positive integer X which Kiki was counting in the sample output format. If there is no solution then output -1.

#include<bits/stdc++.h> 
using namespace std;
#define N 10005
#define ll __int64
ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
void extend_gcd (ll a , ll b , ll& d, ll &x , ll &y) {  
	if(!b){d = a; x = 1; y = 0;}
	else {extend_gcd(b, a%b, d, y, x); y-=x*(a/b);}
}
ll inv(ll a, ll n) {
	ll d, x, y;
	extend_gcd(a, n, d, x, y);
	return d == 1 ? (x+n)%n : -1;
}
ll n[N],b[N],len,lcm;
ll work(){
	for(ll i = 2; i <= len; i++) {
		ll A = n[1], B = n[i], d, k1, k2, c = b[i]-b[1];
		extend_gcd(A,B,d,k1,k2);
		if(c%d)return -1;
		ll mod = n[i]/d;
		ll K = ((k1*(b[i]-b[1])/d)%mod+mod)%mod;
		b[1] = n[1]*K + b[1];
		n[1] = n[1]*n[i]/d;
	}
	if(b[1]==0)return lcm;
	return b[1];
}
int main(){
	ll i,T,Cas=1;cin>>T;
	while(T--){
		cin>>len;
		lcm = 1;
		for(i=1;i<=len;i++) {
			cin>>n[i];
			lcm = lcm / gcd(lcm,n[i]) * n[i];
		}
		for(i=1;i<=len;i++)cin>>b[i];
		cout<<"Case "<<Cas++<<": ";
		cout<<work()<<endl;
	}
	return 0;
}

三：快速幂模m算法

A:整数快速幂

$a^b$ = $a^{b_n{2}^n+b_{n-1}{2}^{n-1}+\cdots +b_{1}2+b_0}$ = $a^{b_n{2}^n}$$a^{b_{n-1}{2}^{n-1}}$$\cdots$$a^{b_{1}2}$$a^{b_0}$

若$b_n$ = $b_{n-1}$=1 , 则$a^{b_n{2}^n}$ = $a^{b_{n-1}{2}^{n-1}}$$a^{b_{n-1}{2}^{n-1}}$

#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
int qpow (int a,int b)
{
	int ans,base;
	ans=1;
	base=a;
	while(b)
	{
		if(b&1) ans=(ans*base)%mod;  //取二进制b的末位 
		base=(base*base)%mod;       //翻倍 
		b>>=1;                     //移位 
	}
	return ans%mod;
}
int main()
{
	int a,b;
	cin>>a>>b;
	cout<<qpow(a,b)<<endl;
}

B:矩阵快速幂

形如 求A^b //A是矩阵

在斐波拉契数列中
$$\left[\begin{array}{c}F(n)\\ F(n-1)\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]\ast \left[\begin{array}{c}F(n-1)\\ F(n-2)\end{array}\right]$$

$$\left[\begin{array}{c}F(n)\\ F(n-1)\end{array}\right]=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]{}^{n-1}\ast \left[\begin{array}{c}F(n-1)\\ F(n-2)\end{array}\right]$$

include<bits/stdc++.h>
using namespace std;
 
const int maxn=2;//阶数 
const int mod=100007;
 
//矩阵结构体 
struct ma//matrix矩阵 
{
    int a[maxn][maxn];
    void init()
	{    //初始化为单位矩阵 
        memset(a,0,sizeof(a));
        for(int i=0;i<maxn;++i) a[i][i] = 1;
    }
};
 
//矩阵乘法 
ma mul(ma a, ma b)
{
    ma ans;
    for(int i=0;i<maxn;++i)
	{
        for(int j=0;j<maxn;++j)
		{
            ans.a[i][j] = 0;
            for(int k=0;k<maxn;++k)
			{
                ans.a[i][j]+=a.a[i][k]*b.a[k][j];
                ans.a[i][j]%=mod; 
            }
        }
    } 
    return ans;
}
 
//矩阵快速幂 
ma qpow(ma a,int n)
{
    ma ans;
    ans.init();
    while(n)
	{
        if(n&1) ans=mul(ans,a);
        a=mul(a,a);
        n>>=1;
    } 
    return ans;
}
 
void output(ma a)
{
    for(int i=0;i<maxn;++i)
	{
        for(int j=0;j<maxn;++j) cout<<a.a[i][j]<<" ";
        cout<<endl;
    }
}
 
int main()
{
	int n;
    ma a;
    a.a[0][0]=1;
    a.a[0][1]=1;
    a.a[1][0]=1;
    a.a[1][1]=0;
    cin>>n;
    ma ans=qpow(a,n); 
    output(ans);//第n个矩阵 
    cout<<ans.a[0][1];//第n个斐波那契数 
    return 0;
}

四：中国剩余定理

中国剩余定理学习