
Author| Rickyの水果摊
Time | 2022.9.3
Lecture 3: Multiplication and inverse matrices
Lecture Info
-
Instructor: Prof. Gilbert Strang
-
Course Number: 18.06
-
Topics: Linear Algebra
-
Official Lecture Resource: Resource Index of Linear Algebra
Excellent Notes on GitHub
There are some classic, excellent notes from other authors on GitHub, wihch I highly recommend you to star ⭐️ and read 📖
notes-linear-algebra (A systematic notes written in Chinese)
The-Art-of-Linear-Algebra (Focus on visualization of important concept of Linear Algebra)
Video Link
Key Points
-
4 ways to understand matrix multiplication
-
matrix inverses
-
magic of Guass - Jordan Guess
Active Recall Questions
- What’s the underlying fundamentals behind 4 ways of matrix multiplication ? (Hint: draw the multiplication pictures)
- When we talk about A − 1 A^{-1} A−1 , what’s the premise of A A A ? (Hint: size of A, invertibility) ❗️
- When is a square matrix not invertible?
- If A , B A,B A,B are inverseble, how to deduce the formula ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1 ?
- If A , B A,B A,B are inverseble, how to deduce the formula ( A B ) T = B − T A − T (AB)^{T}=B^{- T}A^{- T} (AB)T=B−TA−T ?
- How to determine A − 1 A^{-1} A−1 ? Can you replay the process of Guass - Jordan guess ? Why we can determine A − 1 A^{-1} A−1 by Guass - Jordan guess ?
Answer
-
Figures below are from kenjihiranabe 's excellent repository The-Art-of-Linear-Algebra (Which I highly recommend you to star ⭐️)
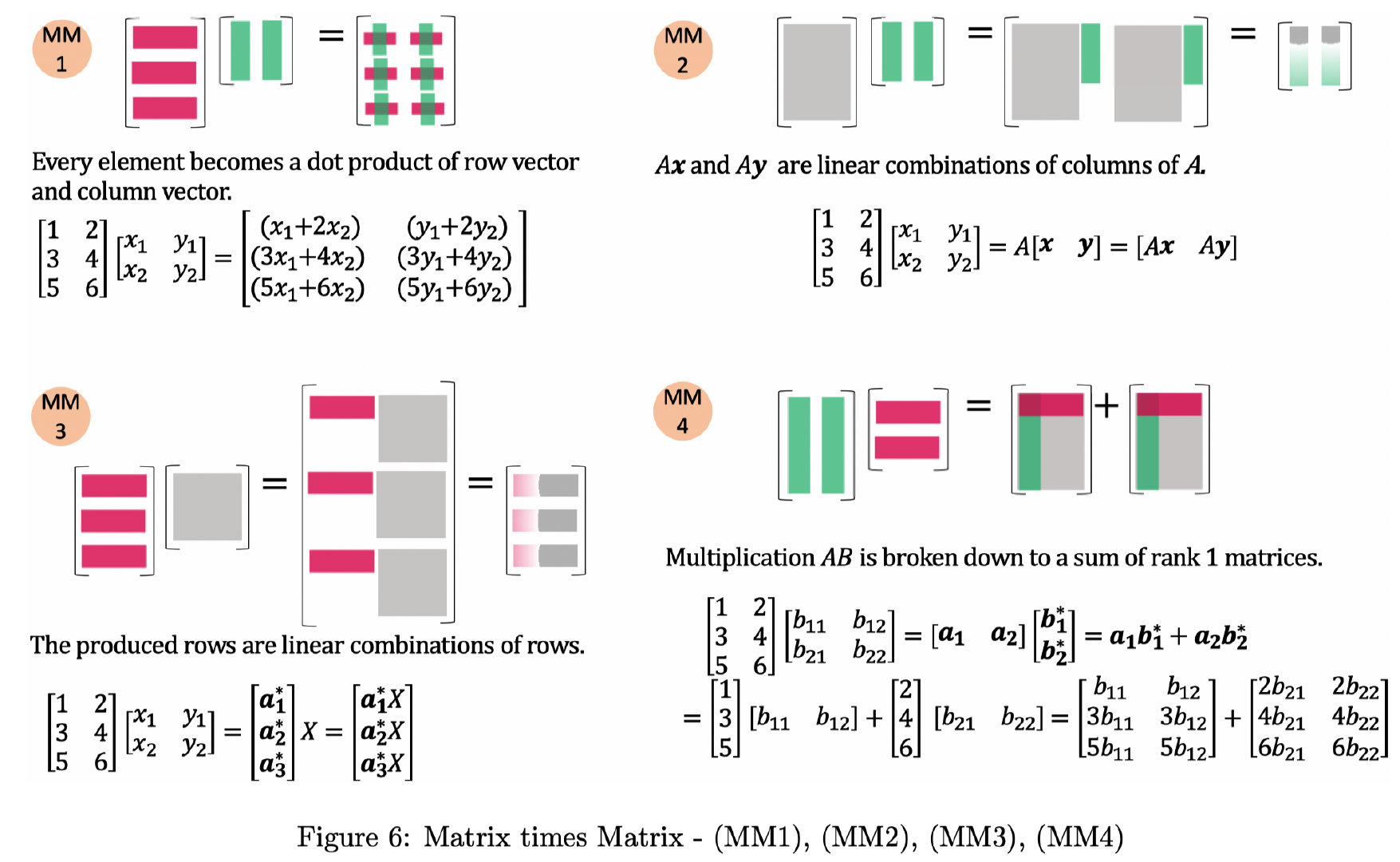
-
A A A must be an invertible square matrix. (or non-singular matrix)
-
A n ∗ n A_{n*n} An∗n have n pivots / r a n k ( A ) = n rank(A)=n rank(A)=n / all the column vectors in A A A are independent
-
Here is the derivation:
- A B AB AB
- B − 1 A − 1 ( A B ) = B − 1 ( A − 1 A ) B = B − 1 I B = B − 1 B = I B^{-1}A^{-1}(AB)=B^{-1}(A^{-1}A)B=B^{-1}IB=B^{-1}B=I B−1A−1(AB)=B−1(A−1A)B=B−1IB=B−1B=I
- ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
-
We know on the one hand that ( A B ) j i T = ( A B ) i j T , (AB)_{ji}^T=(AB)_{ij}^T, (AB)jiT=(AB)ijT, hence
( A B ) i j T = ( A B ) j i = ∑ k = 1 n a j k b k i (A B)_{i j}^{T}=(A B)_{j i}=\sum_{k=1}^{n} a_{j k} b_{k i} (AB)ijT=(AB)ji=k=1∑najkbki
on the other hand
( B T A T ) i j = ∑ k = 1 n b i k T a k j T = ∑ k = 1 n b k i a j k = ∑ k = 1 n a j k b k i \left(B^{T} A^{T}\right)_{i j}=\sum_{k=1}^{n} b_{i k}^{T} a_{k j}^{T}=\sum_{k=1}^{n} b_{k i} a_{j k}=\sum_{k=1}^{n} a_{j k} b_{k i} (BTAT)ij=k=1∑nbikTakjT=k=1∑nbkiajk=k=1∑najkbki
so, since ( A B ) i j T = ( B T A T ) i j (A B)_{i j}^{T}=\left(B^{T} A^{T}\right)_{i j} (AB)ijT=(BTAT)ij for all i = 1 , … m i=1,\dots m i=1,…m and j = 1 , … n j=1,\dots n j=1,…n we have
( A B ) T = B T A T (AB)^T=B^TA^T (AB)T=BTAT -
[ A ∣ I ] = > [ I ∣ A − 1 ] \begin{bmatrix} A|I \end{bmatrix}=>\begin{bmatrix} I|A^{-1}\end{bmatrix} [A∣I]=>[I∣A−1]
- When we do row elimination, we are actually multiply a sets of elementary matrices E n ∗ n . . . E 31 E 21 = E f i n a l E_{n*n}...E_{31}E_{21}=E_{final} En∗n...E31E21=Efinal to [ A ∣ I ] \begin{bmatrix} A|I \end{bmatrix} [A∣I].
- We get [ E f i n a l × A ∣ E f i n a l × I ] = [ I ∣ ? ] \begin{bmatrix} E_{final} \times A|E_{final} \times I \end{bmatrix}=\begin{bmatrix} I|?\end{bmatrix} [Efinal×A∣Efinal×I]=[I∣?]
- E f i n a l × A = I = > E f i n a l = A − 1 E_{final} \times A=I=>E_{final}=A^{-1} Efinal×A=I=>Efinal=A−1, at the same time E f i n a l × I = E f i n a l = ? = A − 1 E_{final} \times I = E_{final}=?=A^{-1} Efinal×I=Efinal=?=A−1
- That the magic of Guass - Jordan guess

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








