一、基本思路
1、应用条件
- 值域很大,如 0 ~ 10^9
- 个数很少,如 0 ~ 10^5
2、举例
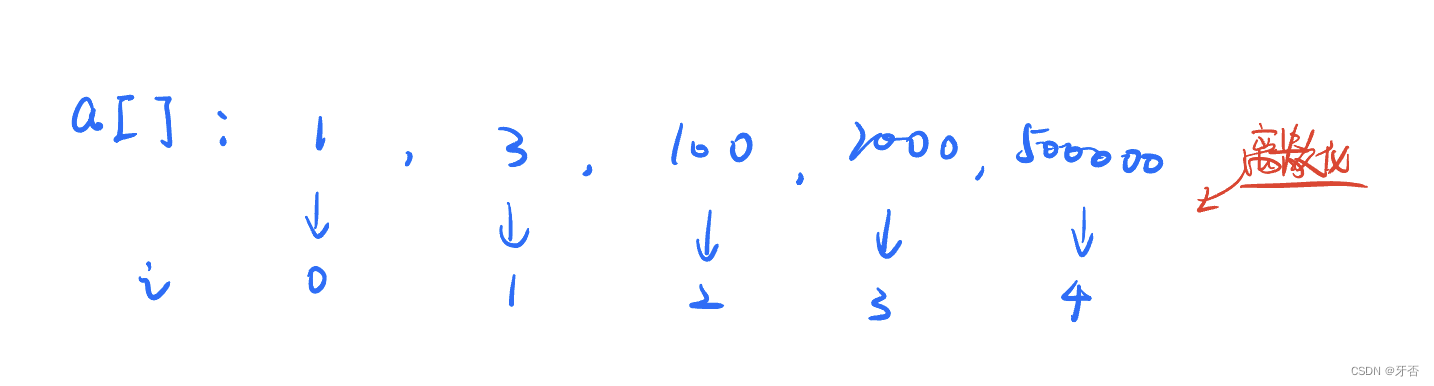
- 注意此处是进行 index 的离散化,并且还需要进行一个离散化后的数组存储
3、算法原理
(1)a[ ] 可能存在重复元素
(2)如何计算原序列 index 离散化之后的值
-
1. 对原数组插入索引(包括需要查询的索引)进行排序
-
2. 进行索引判重 unique,返回非重复元素的离散数组的索引
-
3. 根据返回索引,删除重复元素
-
4. 根据二分法求解原序列索引 index 对应的离散化值(找到从左向右第一个大于等于index的离散化值对应的新索引)
-
5. 对需要查询的值也进行二分查找离散化值
二、Java、C语言模板实现
import java.util.*;
public class Main {
public static int unique(List<Integer> list){
int j = 0;
for (int i = 0; i < list.size(); i++) {
if (i == 0 || list.get(i) != list.get(i - 1)){
list.set(j, list.get(i));
j++;
}
}
return j;
}
public static int find(int index, List<Integer> list){
int left = 0;
int right = list.size() - 1;
while (left < right){
int mid = left + right >> 1;
if (list.get(mid) >= index){
right = mid;
}else {
left = mid + 1;
}
}
return left + 1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int N = 3000010;
int[] a = new int[N];
int[] s = new int[N];
List<Integer> allIndex = new ArrayList<>();
List<Pair> add = new ArrayList<>();
List<Pair> query = new ArrayList<>();
for (int i = 0; i < n; i++) {
int x = scanner.nextInt();
int c = scanner.nextInt();
add.add(new Pair(x, c));
allIndex.add(x);
}
for (int i = 0; i < m; i++) {
int left = scanner.nextInt();
int right = scanner.nextInt();
query.add(new Pair(left, right));
allIndex.add(left);
allIndex.add(right);
}
Collections.sort(allIndex);
int end = unique(allIndex);
allIndex = allIndex.subList(0, end);
for (Pair item : add) {
int index = find(item.first, allIndex);
a[index] += item.second;
}
for (int i = 1; i <= allIndex.size(); i++) {
s[i] = s[i - 1] + a[i];
}
for (Pair item : query) {
int left = find(item.first, allIndex);
int right = find(item.second, allIndex);
System.out.println(s[right] - s[left - 1]);
}
}
}
class Pair{
int first;
int second;
Pair(int x, int y){
this.first = x;
this.second = y;
}
}
```c
vector<int> alls;
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
int find(int x)
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
三、注意事项
- 主要算法步骤:排序 + 去重 + 二分索引离散化
- 其余细节问题在代码注释中已经体现
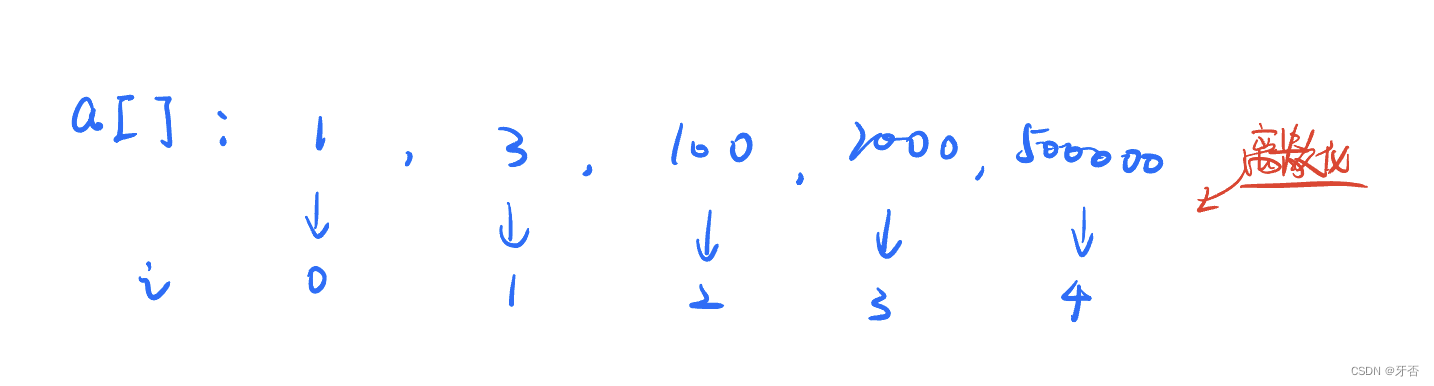








 文章介绍了离散化算法的基本思路,包括应用条件、举例和算法原理,特别强调了处理重复元素和计算离散化值的方法。提供了Java和C语言的模板实现,涉及排序、去重、二分查找等技术,并通过前缀和计算区间和。
文章介绍了离散化算法的基本思路,包括应用条件、举例和算法原理,特别强调了处理重复元素和计算离散化值的方法。提供了Java和C语言的模板实现,涉及排序、去重、二分查找等技术,并通过前缀和计算区间和。

















 1384
1384

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










