数据结构：图（附C++实现代码）

图的定义

• 由非空顶点集V和边集E组成，记为$G=(V,E)$，$E(G)$表示图G中顶点间的关系几何， E = { ( u , v ) ∣ u ∈ V , v ∈ V } E=\left \{ (u,v) | u \in V, v \in V \right \} E={(u,v)∣u∈V,v∈V}。根据边是否有方向分为无向图和有向图。根据是否有重复边可以分为简单图和多重图。
  
• 相关定义：
  • 依附于顶点的边的个数，被称为顶点的度；
  • 定点间如果有可达路径，被称为连通，如果两个顶点互相都可达，称为强连通。对于无向图，如果任意顶点间都是连通的，称为连通图。对于有向图，如果任意间都是强连通的称为强连通图
  • 对于边较多的称为稠密图，边较少的称为稀疏图，二者没有明确边界

图的存储方法

• 邻接矩阵法：存储一个$n\times n$的矩阵，点$(i,j)$代表顶点i与顶点j之间有无边，无向图的邻接矩阵是对称矩阵。如果是有权图，矩阵中可以存储边的权值。这种方法复杂度为$O(n^2)$比较适合存储稠密图，
  

  • 如果用0来表示无边，1表示有边，邻接矩阵A的n次方中的点(i,j)表示从i到j长度为n的路径数量。

• 邻接表：定义顶点类和边类，顶点类存储顶点信息维护一个指针指向边类，边类存储边的信息维护一个指针指向下一条边。与树的孩子表示法类似。
  

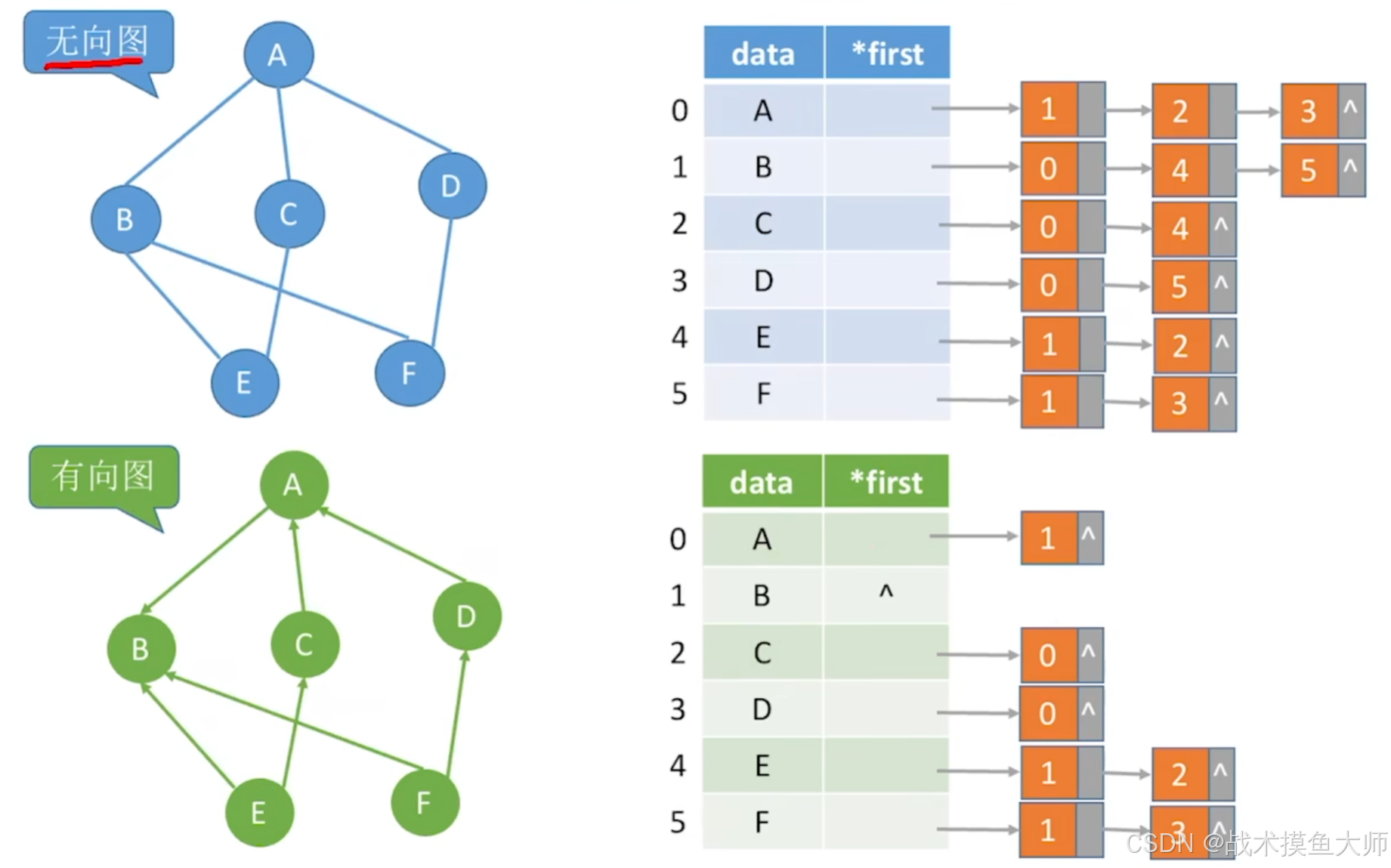
  • 复杂度$O(V+E)$，适合存储稀疏图，找指向某个顶点的所有边不太方便。

• 十字链表(只能用于存储有向图)：跟上面的邻接表类似，在尾节点相同的边之间也维持了一个链表
  

• 邻接多重表(无向图)：跟十字链表类似
  

图的相关操作

图的应用

• 深度学习：神经网络在训练时需要进行反向传播更新梯度，可以使用图的形式存储神经网络，每个中间数据就是图的一个节点，每个操作就是一条边，这样设计便于进行i求导和梯度更新。在推理时，可以将图中可以合并的多个边和节点合并成一个，提高计算效率，这一步骤称为模型推理的图优化阶段。例如$z=sigmod(y),y=wx+b$，可以合并成$z=sigmod(wx+b)$。
• 自动驾驶：路径规划时，可以将路径空间建模为一个图，在图中查找满足约束的最优路径，将路径规划问题建模为查找图中最短路径的问题。

C++代码实现

邻接矩阵存储

#include <iostream>
#include <vector>
#include <unordered_map>

using namespace std;

constexpr int kNoEdge = 0;
enum class GraphType{
    kDigraph,
    kUndigraph,
};

/// @brief 邻接矩阵法实现，临界矩阵中0表示无边，其他表示权重
template<typename T>
class Graph{
public:
    Graph(vector<T> vertexs, vector<vector<int>> edges, GraphType graphtype) : vertexs_(vertexs), edges_(edges), graphtype_(graphtype) {
        for(int i=0;i<vertexs_.size();i++){
            vertex_indexs_[vertexs_[i]] = i;
        }
    }
    bool Adjacent(T x,T y) const;
private:
    GraphType graphtype_;
    vector<T> vertexs_;
    unordered_map<T, int> vertex_indexs_;
    vector<vector<int>> edges_;
};

template<typename T>
bool Graph<T>::Adjacent(T x, T y) const
{
    auto iter = vertex_indexs_.find(x);
    if(iter == vertex_indexs_.end()){
        cout << "Error Vertex" << endl;
        return false;
    }
    int index1 =  iter->second;
    iter = vertex_indexs_.find(y);
    if(iter == vertex_indexs_.end()){
        cout << "Error Vertex" << endl;
        return false;        
    }
    int index2 = iter->second;
    return edges_[index1][index2];
}

int main()
{
    vector<string> vertexs = {"home","school","KTV"};
    vector<vector<int>> edges = {{0,1,1},{1,0,0},{1,0,0}};
    Graph<string> test_map(vertexs,edges,MapType::kUndigraph);
    cout << test_map.Adjacent("school","KTV") << endl;
    cout << test_map.Adjacent("school","home") << endl;
    return 0;
}

邻接表实现

#include <iostream>
#include <vector>
#include <unordered_map>
#include <string>
#include <memory>

using namespace std;

enum class MapType{
    kDigraph,
    kUndigraph
};

class Edge{
public:

    Edge(int start_vertex_id,int end_vertex_id) : 
        value_(1.0),
        next_edge_(nullptr),
        start_vertex_id_(start_vertex_id),
        end_vertex_id_(end_vertex_id) {}
    ~Edge() {
        if(next_edge_ != nullptr){
            delete next_edge_;
        }
    };
// private:
    double value_;
    int start_vertex_id_;
    int end_vertex_id_;
    Edge* next_edge_;
};

// 定义图中顶点的数据结构
template<typename T>
class Vertex {
public:
    Vertex(T data) : data_(data) {}
    Vertex(T data, int id) : data_(data), vertex_id_(id) {}
    bool AddEdge(int end_vertex_id){
        if(edges_ == nullptr){
            edges_ = make_shared<Edge>(vertex_id_,end_vertex_id);
        }else{
            Edge* temp = edges_.get();
            while(temp->next_edge_ != nullptr){
                if(temp->end_vertex_id_ == end_vertex_id) { return false;}
                temp = temp->next_edge_;
            }
            if(temp->end_vertex_id_ == end_vertex_id) { return false;}
            temp->next_edge_ = new Edge(vertex_id_,end_vertex_id);
        }
        return true;
    }

    bool Adjacent(int end_vertex_id){
        Edge* temp = edges_.get();
        while(temp != nullptr){
            if(temp->end_vertex_id_ == end_vertex_id) { return true;}
            temp = temp->next_edge_;
        }
        return false;
    }
// private:
    T data_;
    int vertex_id_;
    shared_ptr<Edge> edges_;
};

template<typename T>
class Graph {
public:
    Graph() : type_(MapType::kDigraph) {};
    bool AddVertex(Vertex<T> input){
        if(vertex_index_.find(input.data_) != vertex_index_.end()){return false;}
        vertex_index_[input.data_] = vertexs_.size();
        input.vertex_id_ = vertexs_.size();
        vertexs_.emplace_back(input);
        return true;
    }
    bool AddEdge(T start, T end){
        auto iter = vertex_index_.find(start);
        if(iter == vertex_index_.end()){return false;}
        int start_id = iter->second;
        iter = vertex_index_.find(end);
        if(iter == vertex_index_.end()){return false;}
        return vertexs_[start_id].AddEdge(iter->second);
    }
    bool Adjacent(T start, T end){
        auto iter = vertex_index_.find(start);
        if(iter == vertex_index_.end()){return false;}
        int start_id = iter->second;
        iter = vertex_index_.find(end);
        if(iter == vertex_index_.end()){return false;}
        return vertexs_[start_id].Adjacent(iter->second);
    }
// private:
    MapType type_;
    vector<Vertex<T>> vertexs_;
    unordered_map<T,int> vertex_index_;

};

int main() {
    Vertex<string> home("home");
    Vertex<string> school("school");
    Vertex<string> KTV("KTV");
    Graph<string> graph;
    graph.AddVertex(home);
    graph.AddVertex(school);
    graph.AddVertex(KTV);
    graph.AddEdge("home","school");
    graph.AddEdge("home","KTV");
    cout << graph.Adjacent("home","school") << endl;
    return 0;
}

Ref

王道考研408-数据结构