递归调用实例

• 迷宫问题：规定0表示没有障碍，而1表示有障碍

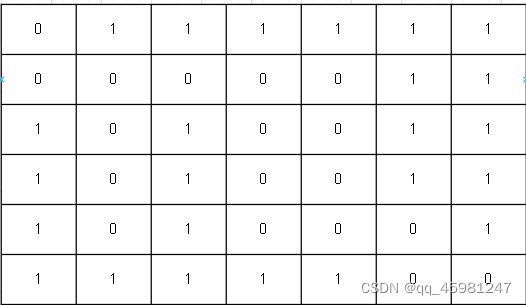
要求从左上角到达右下角：

1）先将这个“迷宫”存储到二维数组中

int [][]arr= {	
				{0,1,1,1,1,1,1,},
				{0,0,0,0,0,1,1,},
				{1,0,1,0,0,1,1,},
				{1,0,1,0,0,1,1,},
				{1,0,1,0,0,0,1,},
				{1,1,1,1,1,0,0,},
									};
		
		for(int i=0;i<arr.length;i++) {//输出康康
			for(int j=0;j<arr[i].length;j++) {
				System.out.print(arr[i][j]+" ");
			}
			System.out.println();
		}

2）创建一个迷宫类，定义一个方法GetWay

3）确定方法的返回值类型以及参数，且定返回值为boolean，找到了即返回true，没有找到则返回false。传入参数为，迷宫的二维数组，以及当前数组进行遍历的位置。

4）将走过且能走通的路将0赋值为2，当走过却不能走通的路赋值为3.我们是从arr[0][0]开始走的，而终止条件就是能够遍历到arr[6][5]且其值为2的时候。

5）确定遍历的方向，一次只能从上下左右中挑取一个方向进行操作，暂且将遍历方向定位上，右，下，左即顺时针方向，这里会有一个问题，如果进行方向操作会有可能出现数组溢出的异常，所以我们再进行操作的时候还需要判定进行操作的位置是否合法，如不合法直接退出

现在先明确目标是解决这个问题，先找出一条路。所以不要想得太多，优先解决问题

public boolean GetWay(int [][]arr,int i,int j) {
		if(arr[5][6]==2) {//判定的终结条件
			return true;//返回成功到达终点
		}else {//如果并没有遍历到最后的终点，则继续进行下一个点的递归操作
			if(arr[i][j]==0) {//判断当前点是否能走，能走进行递归操作，
                              //不能则注意配对的else进行什么操作-》
				arr[i][j]=2;//假定该位置可以走
				//那么进行下一个位置的判定，则开始递归，递归方向为上、右、下、左
				//在进行判断之前，先要判断被判断的位置是否是在该数组中
				if(In(arr,i-1,j)&&GetWay(arr,i-1,j)) {//后面递归的位置其实是它的上面一个
					return true;//这里你可以将(i,j)看作一个坐标，它的上方即坐标为(i-1,j)
				}else if(In(arr,i,j+1)&&GetWay(arr,i,j+1)) {//同理这里进行遍历它的右边
					return true;
				}else if(In(arr,i+1,j)&&GetWay(arr,i+1,j)) {//同理这里进行遍历它的下边
					return true;
				}else if(In(arr,i,j-1)&&GetWay(arr,i,j-1)) {//同理这里进行遍历它的左边
					return true;
				}else {
					arr[i][j]=3;//添加一个遍历过的标记
					return false;
				}	
			}
			else {//-》与上面配对的if操作，这里代表的是遍历到arr[i][j]的值为1或2或3
                  //为1代表障碍不能进行操作，为2或者3均代表了这里已经被遍历过了，
                  //再次遍历,直接结束。
				return false;
			}
		}
	}
	public boolean In(int [][]arr,int i,int j) {//判定arr[i][j]是否越界
		if(i>=0&&i<arr.length&&j>=0&&j<arr[i].length) {
			return true;
		}else {
			return false;
		}
	}

输出的结果为：

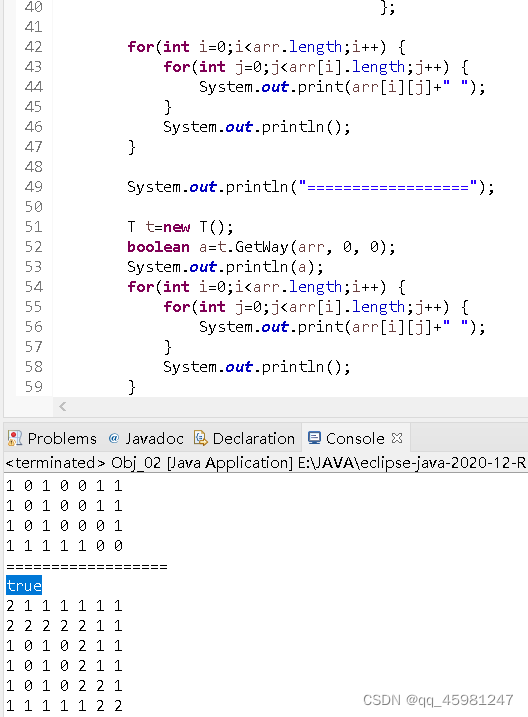
 有人可能就会问：为啥你的地图上没有3嘞，

我们就需要站在程序的角度思考一下，我们是先对这个“迷宫”的一个点进行的上、右、下、左这个顺序进行遍历的，第一个点只能向下，成功到达下一个点则再对其进行上、右、下、左刚好直接一条路就通过了，不妨将顺序换一下。将其转化为上、左、下、右的顺序即逆时针。

结果：

果然，这个3就有了，需要注意补3其实体现出了一种回溯的思想，在哪里补，用什么补，在不同的题目是不同的，这里补的3，就相当于是程序遍历过这里所留下的一个标记。

这只是我的思路进行解决这个问题，现在我对解题方法的解释就是“管他黑猫，白猫能抓到老鼠就是好猫”。找到一种解决方法就进行尝试，能解决我当前问题即可，对程序的优化那都是后话。