文章索引
写在前面
本文主要描述二叉树的创建和遍历,并以此加深对dfs和bfs的理解。
二叉树的创建一般分为从根开始插入(多用于创建搜索树及其分化),和不断连接子树多用于创建一般树。
不论怎么遍历二叉树,都是从根开始并且每个结点都仅仅是被访问一次,只是算法和访问顺序的变化才形成前、中、后、层序遍历这几种遍历说法罢了。究其本质:就是bfs和dfs,因此加深对dfs和bfs的理解才是最主要的。
二叉树的创建
1.如何创建二叉树
①前面 https://editor.youkuaiyun.com/md/?articleId=107633966 谈到二叉树有顺序和链式存储方式,但顺序存储方式不适合普通的二叉树,因此我们采用链式存储方式;
②建二叉树,既然是树,可以首先从根考虑。然后便可以通过向这个树一直插入结点即可创建一颗树,例如:构建一颗二叉查找树的过程

第二:也可以通过从叶结点开始,制造出一颗颗小树最后连成一颗大树

二叉树的遍历
1、二叉树的遍历一般可分为 前序遍历,中序遍历,后序遍历,层序遍历。
① 虽然是4中遍历,但其实前三种就是深度优先搜索算法的应用(dfs),后者为广度优先算法的应用(bfs)
只要理解这两种算法,那这几种遍历都可以理解了。
一:深度优先搜索算法(英语:Depth-First-Search,简称DFS)是一种用于遍历或树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n),DFS搜索的过程访问可以称之为DFS序。
简单说来就是:从起始结点开始朝一个方向一直深入(向下),然后回头继续走上一段路的邻路又一直深入……,直到走完所有路 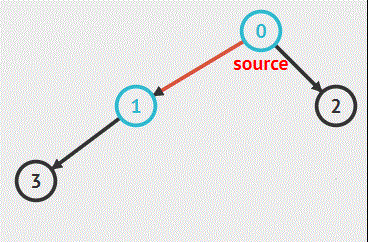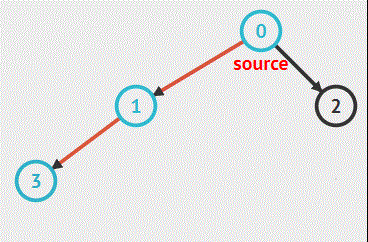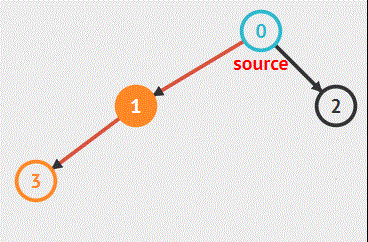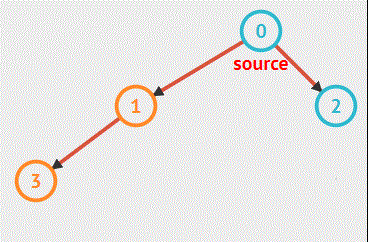

因此这样就可以用递归实现dfs了;
2、前序中序后序的实现原理
而前序、中序、后序遍历是什么呢?
前序遍历:访问根结点;按前序遍历左子树 ;按前序遍历右子树。
中序遍历:按中序遍历左子树;访问根结点;按中序遍历右子树。
后序遍历:按后序遍历左子树; 按后序遍历右子树; 访问根结点。
从定义不难发现,这是一个递归的定义 ,也就是在dfs的基础上多加了一个visit
那完全也可以按dfs的流程来理解 这三种遍历方法。
!
比如这颗数的前、中、后序遍历结果为:
ABDFECGHI
DBEFAGHCI
DEFBHGICA
✧图中在从入口到出口的曲线上用区、★和△三种符 号分别标
记出了先序、中序和后序访问各结点的时刻 从以上结果不难发现,dfs遍历顺序会经过同一个结点三次,前序就是第一次经过结点时访问,中序是第二次经过结点时访问,而后序则是第三次经过结点时访问;
从以上结果不难发现,dfs遍历顺序会经过同一个结点三次,前序就是第一次经过结点时访问,中序是第二次经过结点时访问,而后序则是第三次经过结点时访问;
例如分析B结点:A->B 一次,D->B回溯一次,F->B回溯一次,共三次。
也就是说: 其父节点向下遍历经过一次,其两个子节点回溯两次,共三次
从以上分析:实现难点也就是上一个结点(父节点信息保存),以便遍历完子树进行回溯,而这恰好就是一个先进后出的模型。因此可用递归和栈实现。
3.递归实现先、中、后序遍历
只用改变Visit的相对位置放到前、中、后,就可以做到先、中、后序遍历了, 递归的先中后遍历,才用定义的先序先访问后递归访问,中序先递归访问再访问,后序先两次递归访问再访问’
4.栈实现先中后序
1.先、中序实现
实现栈的代码,则考虑用第二种理解方式。也就是:前序就是第一次经过结点时访问,中序是第二次经过结点时访问,而后序则是第三次经过结点时访问 ;
利用栈先进后出保存父节点,实现dfs;
可怎么入栈呢?
通过第二种理解方式,遇到结点第一次便是入栈,第二次遇到结点便出栈这样就可以实现这先、中序,这样便保留了一次遍历,一次回溯的时刻,即可完成先、中序


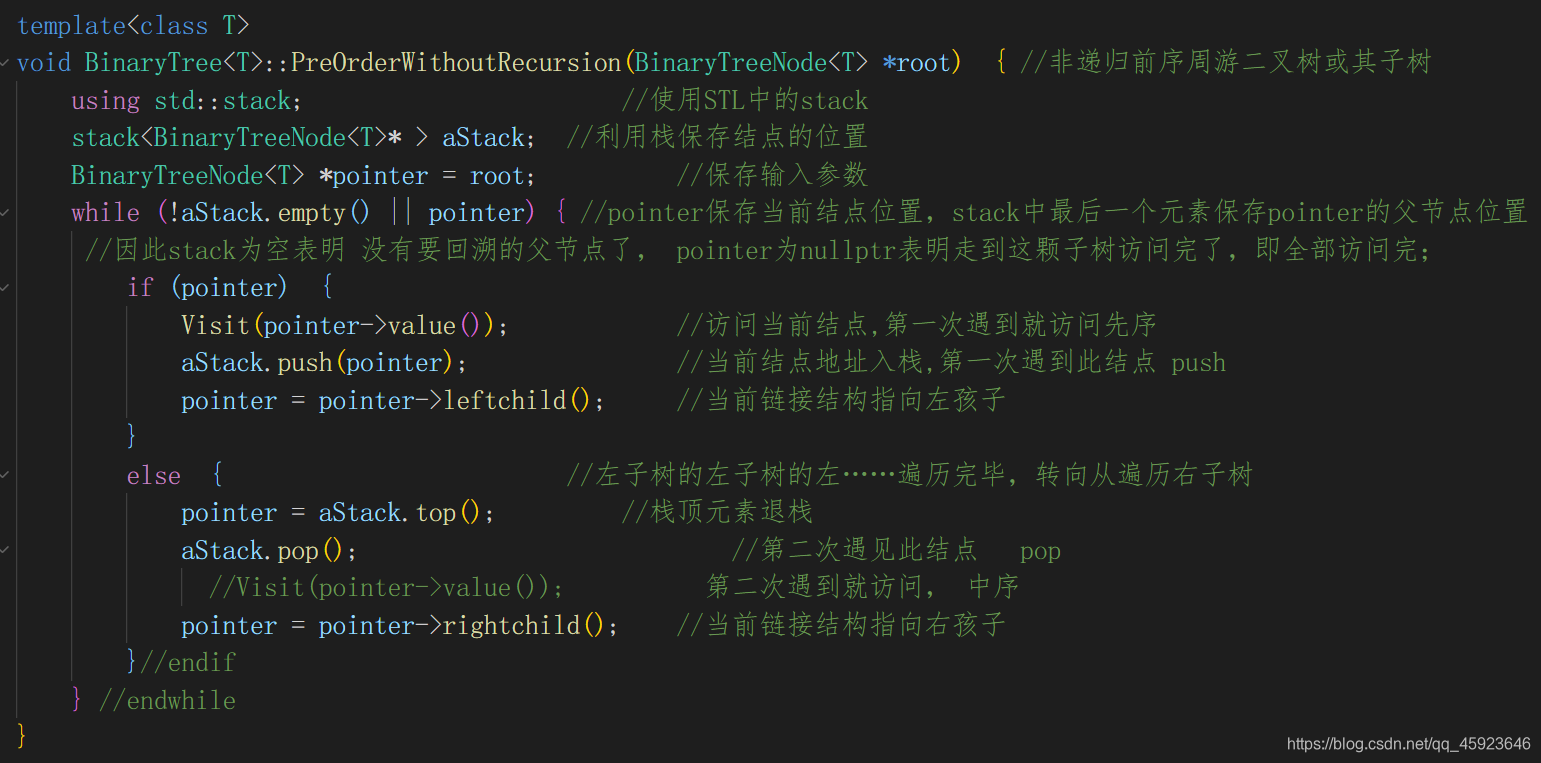
2.栈实现二叉树后序遍历
先序、中序已经保留前两次遇到的位置的时刻了,要实现后序,那就是要再多保存一个第三次遇到的时刻即可
那如何保存第三次结点的时刻呢? 不妨再看一遍这幅图,会发现第一次回溯是遍历完了左子树,第二次则是遍历完了右子树,因此引入一个标记变量即可判断是否是第二次回溯

在保留指针的基础上,多加一个枚举类型即可(普通类型也无大碍)

前一次遍历,和回溯是和前后序类似的。

判断是哪次回溯只需引入一个if即可

enum Tags {Left, Right}; //枚举类型
//用于非递归的后序遍历
template <class T>
class StackElement { //StackElement
public:
BinaryTreeNode<T> *pointer; //保存当前结点
Tags tag; //标志位,在非递归后序周游二叉树时 用来判断是Left还是Right回溯
};
template<class T>
void BinaryTree<T>::PostOrderWithoutRecursion(BinaryTreeNode<T> *root) {//非递归后序周游二叉树或其子树
using std::stack; //使用STL栈部分
StackElement<T> element; //中间变量
stack<StackElement<T > > aStack; //栈申明
BinaryTreeNode<T> *pointer;
if (root == nullptr)
return; //空树即返回
else pointer = root; //保存输入参数
while (!aStack.empty() || pointer) {
while (pointer != nullptr) { //深度一直搜直到左子树的左子树……为nullptr
element.pointer = pointer; //保留当前结点信息
element.tag = Left; //标记为 左孩子
aStack.push(element); //第一次遇到此结点,push
pointer = pointer->leftchild(); //沿左子树方向向下周游
}
element = aStack.top(); //开始回溯
aStack.pop(); //托出栈顶元素,第二次遇到此结点pop()
pointer = element.pointer;
if (element.tag == Left) { //标记位位 Left 从左子树回来(是第一次回溯),接着去访问右子树
element.tag = Right; //标记为右子树
aStack.push(element); //相当于把刚才 出栈的那个元素 换一个标记
pointer = pointer->rightchild(); //同样方式遍历右孩子
}
else { //从右子树回来 ,第三次遇到此节点
Visit(pointer->value()); //第二次回溯了,可以访问当前结点了
pointer = nullptr; //以为着一颗子树已经遍历完了,可以 回溯了(如果未遍历完)
}
}
}
5.二叉树的层序遍历
层序遍历:从二叉树的第0层(根结点)开始,自上至下逐层遍历;在同一层中,按照从左到右的顺序对结点逐一访问。 简而言之:从根节点开始一层一层从左往右走到无路可走,又从下一层开始这样走,直到走完这棵树
例如遍历这样一棵二叉树:
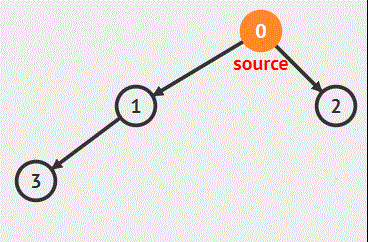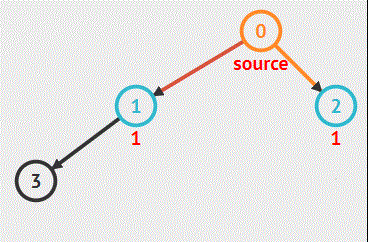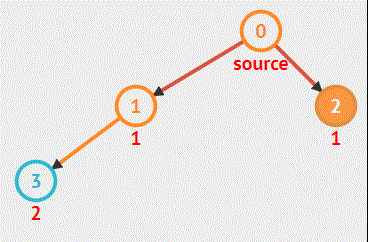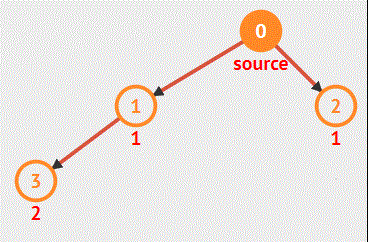
而这正好就是 宽度优先搜索算法的一种表现形式、宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一。
层序基本过程:
①先根结点入队
②从队列中取出一个元素;
③访问该元素所指结点;
④若该元素所指结点的左、右孩子结点非空,则将其左、右孩子的指针顺序入队。

简而言之就是, 借助队列的先进先出的特点存储儿子结点,然后遍历完这层的所有兄弟结点,再出队从左往右遍历儿子结点,以此往复直到遍历完整棵树。

二叉树的创建和遍历代码
1. c实现
#include<stdio.h>
#include<stdlib.h>、
#include"Queue.h"
typedef char ElementType;
typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
typedef struct TNode { /* 树结点定义 */
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
} T;
BinTree CreateTree( ElementType info, BinTree LeftChild, BinTree RightChild)
{
//由左子树leftTree、右子树rightTree和数据元素info创建一棵新树,根结点、是info
//其中this、leftTree、rightTree必须是不同的三棵树
BinTree root = malloc(sizeof(T));
root->Left = LeftChild;
root->Right = RightChild;
root->Data = info;
return root;
}
void InorderTraversal( BinTree BT ) //中序遍历
{
if ( BT ) {
InorderTraversal( BT->Left );
/* 此处假设对BT结点的访问就是打印数据 */
printf("%c ", BT->Data); /* 假设数据为整型 */ //访问完做子树再访问结点
InorderTraversal( BT->Right );
}
}
void PreorderTraversal( BinTree BT ) //前序遍历
{
if ( BT ) {
printf("%c ", BT->Data ); //先访问结点然后再对 左右子树遍历
PreorderTraversal( BT->Left );
PreorderTraversal( BT->Right );
}
}
void PostorderTraversal( BinTree BT ) //后序遍历 ,先遍历完左右子树 再访问结点
{
if ( BT ) {
PostorderTraversal( BT->Left );
PostorderTraversal( BT->Right );
printf("%c ", BT->Data);
}
}
void LevelorderTraversal ( BinTree BT ) //层序遍历, 一层一层地逐层遍历
{
Queue Q; //利用队列 对结点进行保存
BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue(); /* 创建空队列Q */
enQueue( Q, BT ); //入队保存结点
while ( !IsEmpty(Q) ) {
T = deQueueAndFront( Q ); //出队并返回队头元素
printf("%d ", T->Data); /* 访问取出队列的结点 */
if ( T->Left ) enQueue( Q, T->Left ); //左儿子先入队
if ( T->Right ) enQueue( Q, T->Right ); //右儿子后入队 先访问左儿子后访问右儿子
}
}
int main()
{
BinTree a, b, c, d, e, f, g, h, i, nulltree;
a = b = c = d = e = f = g = h = i = nulltree = NULL;
d = CreateTree( 'D', nulltree, nulltree);
g = CreateTree( 'G', nulltree, nulltree);
h = CreateTree( 'H', nulltree, nulltree);
i = CreateTree( 'I', nulltree, nulltree);
f = CreateTree( 'F', h, i);
e = CreateTree( 'E', g, nulltree);
b = CreateTree( 'B', d, e);
c = CreateTree( 'C', nulltree, f);
a = CreateTree( 'A', b, c); //A为根
printf("Preorder sequence is: \n");
InorderTraversal(a);
printf("\n");
//中序周游二叉树
printf( "Inorder sequence is:\n ");
PreorderTraversal(a); //递归
printf("\n");
//后序周游二叉树
printf("Postorder sequence is: \n");
PostorderTraversal(a); //递归
printf("\n");
return 0;
}
2. c++实现
//************SearchBinaryTree****************// 建议分成二个文件
/* BinaryTreeNode.h */
#ifndef BINARY_TREE
#define BINARY_TREE
#include <stack>
#include <queue>
#include<iostream>
template <class T> class BinaryTree; //先声明此类
template <class T>
class BinaryTreeNode {
friend class BinaryTree<T>; //声明二叉树为结点类的友元类,便于访问私有数据成员
private:
T info; //二叉树结点数据域
BinaryTreeNode<T> *left; //二叉树结点指向左子树的指针
BinaryTreeNode<T> *right; //二叉树结点指向左子树的指针
public:
BinaryTreeNode(); //缺省构造函数
BinaryTreeNode(const T &inf); //给定数据的构造函数
BinaryTreeNode(const T &inf, BinaryTreeNode<T> *l, BinaryTreeNode<T> *r); //给定了结点值和左右子树的构造函数
T value() const; //返回当前结点的数据的拷贝
BinaryTreeNode<T> *leftchild() const; //返回当前结点左子树的地址的拷贝
BinaryTreeNode<T> *rightchild() const; //返回当前结点右子树的地址的拷贝
void setLeftchild(BinaryTreeNode<T> *) ; //设置当前结点的左子树
void setRightchild(BinaryTreeNode<T> *) ; //设置当前结点的右子树
void setValue(const T &val); //设置当前结点的数据域
bool isLeaf() const; //判定当前结点是否为叶结点,若是返回true
BinaryTreeNode (const BinaryTreeNode<T> &Node):
info(Node.info), left(Node.left), right( Node.right) { }
//重载赋值操作符
BinaryTreeNode<T> &operator=(const BinaryTreeNode<T> &Node) {//拷贝赋值运算符
info = Node->info;
left = Node.left;
right = Node.right;
return *this;
}
};
//****** BinaryTreeNode Implementation *******//
template<class T>
BinaryTreeNode<T>::BinaryTreeNode(): left(nullptr), right(nullptr) {} //默认初始化
template<class T>
BinaryTreeNode<T>::BinaryTreeNode(const T &inf): info(inf), left(nullptr), right(nullptr) {} //给定数据的构造函数
template<class T>
BinaryTreeNode<T>::BinaryTreeNode(const T &inf, BinaryTreeNode *l, BinaryTreeNode *r) :
info(inf), left(l), right(r) { } //给定数据的左右指针的构造函数
template<class T>
T BinaryTreeNode<T>::value() const { //返回当前结点的数据的拷贝
return info;
}
template<class T>
BinaryTreeNode<T> *BinaryTreeNode<T>::leftchild() const { //返回当前结点指向左子树的指针的拷贝
return left;
}
template<class T>
BinaryTreeNode<T> *BinaryTreeNode<T>::rightchild() const { //返回当前结点指向右子树的指针的拷贝
return right;
}
template<class T>
void BinaryTreeNode<T>::setLeftchild(BinaryTreeNode<T> *subroot) { //设置当前结点的左子树
left = subroot;
}
template<class T>
void BinaryTreeNode<T>::setRightchild(BinaryTreeNode<T> *subroot) { //设置当前结点的右子树
right = subroot;
}
template<class T>
void BinaryTreeNode<T>::setValue(const T &val) { //设置当前结点的数据域
info = val;
}
template<class T>
bool BinaryTreeNode<T>::isLeaf() const { //判定当前结点是否为叶结点,若是返回true
return (left == nullptr) && (right == nullptr);
}
//************BinaryTree****************//
enum Tags {Left, Right}; //枚举类型
//用于非递归的后序遍历
template <class T>
class StackElement { //StackElement
public:
BinaryTreeNode<T> *pointer; //保存当前结点
Tags tag; //标志位,在非递归后序周游二叉树时 用来判断是Left还是Right回溯
};
using namespace std;
template <class T>
class BinaryTree {
private:
BinaryTreeNode<T> *root; //二叉树根结点
public:
BinaryTree(): root(nullptr) {} //构造函数
~BinaryTree() {
DeleteBinaryTree(root); //析构函数,删掉整个二叉树即可
}
void DeleteBinaryTree(BinaryTreeNode<T> *root); //删除二叉树或其子树
void CreateTree(const T &info, BinaryTree<T> &leftTree, BinaryTree<T> &rightTree);
//构造一棵以info为根、leftTree和rightTree为左右子树的新二叉树
BinaryTreeNode<T> *Parent(BinaryTreeNode<T> *current);//返回current的父结点
BinaryTreeNode<T> *LeftSibling(BinaryTreeNode<T> *current); //返回current结点的左兄弟
BinaryTreeNode<T> *RightSibling(BinaryTreeNode<T> *current);//返回current结点的右兄弟
void PreOrder(BinaryTreeNode<T> *root); //前序周游二叉树或其子树
void InOrder(BinaryTreeNode<T> *root); //中序周游二叉树或其子树
void PostOrder(BinaryTreeNode<T> *root); //后序周游二叉树或其子树
void PreOrderWithoutRecursion(BinaryTreeNode<T> *root); //非递归前序周游二叉树或其子树
void InOrderWithoutRecursion(BinaryTreeNode<T> *root); //非递归中序周游二叉树或其子树
void PostOrderWithoutRecursion(BinaryTreeNode<T> *root); //非递归后序周游二叉树或其子树
void LevelOrder(BinaryTreeNode<T> *root); //按层次周游二叉树或其子树
bool isEmpty() const; //判定二叉树是否为空树
BinaryTreeNode<T> *Root() { //返回二叉树根结点
return root;
};
void Visit(T Value) {
std::cout << Value << std::ends;
}; //访问
};
//********** BianryTree Implementation ***********//
template<class T>
bool BinaryTree<T>:: isEmpty() const { //判定二叉树是否为空树
return ( root ? false : true);
}
template<class T>
BinaryTreeNode<T> *BinaryTree<T>::Parent(BinaryTreeNode<T> *current) { //类似于前序遍历寻找current的父结点
using std::stack; //使用STL中的stack
stack<BinaryTreeNode<T>* > aStack;
BinaryTreeNode<T> *pointer = root; //保存输入参数
if (nullptr != root && nullptr != current) { //空树 和空节点没有 父结点
while (!aStack.empty() || pointer) {
if (pointer) {
if (current == pointer->leftchild() || current == pointer->rightchild())
return pointer; //如果当前pointer的孩子就是current,返回parent
aStack.push(pointer); //当前结点地址入栈
pointer = pointer->leftchild(); //当前链接结构指向左孩子
}
else { //左子树的左子树的左……完毕,转向最后的左子树的右子树
pointer = aStack.top(); //栈顶元素退栈
aStack.pop();
pointer = pointer->rightchild(); //当前链接结构指向右孩子
}//endif
} //endwhile
}//endif
std::cerr << "Error,this is a empty tree or empty node!" << std::endl;
}
template<class T>
BinaryTreeNode<T> *BinaryTree<T>::LeftSibling(BinaryTreeNode<T> *current) { //返回current结点的左兄弟
if (current) {
BinaryTreeNode<T> *temp = Parent(current); //返回current结点的父结点
if ((temp == nullptr) || current == temp->leftchild())
return nullptr; //如果父结点为空,或者current就是左结点,返回空
else return temp->leftchild();
}
return nullptr;
}
template<class T>
BinaryTreeNode<T> *BinaryTree<T>::RightSibling(BinaryTreeNode<T> *current) { //返回current结点的右兄弟
if (current) {
BinaryTreeNode<T> *temp = Parent(current);//返回current结点的父结点
if (temp == nullptr || current == temp->rightchild())
return nullptr; //如果父结点为空,或者current没有右兄弟
else return temp->rightchild();
}
return nullptr;
}
template<class T>
void BinaryTree<T>:: CreateTree (const T &info, BinaryTree<T> &leftTree, BinaryTree<T> &rightTree) {
//由左子树leftTree、右子树rightTree和数据元素info创建一棵新树,根结点数据是info
//其中this、leftTree、rightTree必须是不同的三棵树
root = new BinaryTreeNode<T>(info, leftTree.root, rightTree.root); //创建新树
leftTree.root = rightTree.root = nullptr; //原来两棵子树的根结点指空,避免访问
}
template<class T>
void BinaryTree<T>:: DeleteBinaryTree(BinaryTreeNode<T> *root) { //以 后序周游的方式删除二叉树
if (root) {
DeleteBinaryTree(root->left); //递归删除左子树
DeleteBinaryTree(root->right); //递归删除右子树
delete root; //删除父(根)结点
}
}
template<class T>
void BinaryTree<T>::PreOrder (BinaryTreeNode<T> *root) { //前序周游二叉树
if (root != nullptr) {
Visit(root->value()); //访问当前结点,先序
PreOrder(root->leftchild()); //遍历左子树
//Visit(root->value()); //访问当前结点,中序
PreOrder(root->rightchild()); //遍历右子树
//Visit(root->value()); //访问当前结点,后序
}
}
template<class T>
void BinaryTree<T>:: InOrder (BinaryTreeNode<T> *root) { //中序周游二叉树
if (root != nullptr) {
InOrder (root->leftchild()); //遍历左子树
Visit(root->value()); //访问当前结点
InOrder (root->rightchild()); //遍历右子树
}
}
template<class T>
void BinaryTree<T>:: PostOrder (BinaryTreeNode<T> *root) { //后序周游二叉树
if (root != nullptr) {
PostOrder(root->leftchild()); //遍历左子树
PostOrder (root->rightchild()); //遍历右子树
Visit(root->value()); //访问当前结点
}
}
template<class T>
void BinaryTree<T>::PreOrderWithoutRecursion(BinaryTreeNode<T> *root) { //非递归前序周游二叉树或其子树
using std::stack; //使用STL中的stack
stack<BinaryTreeNode<T>* > aStack; //利用栈保存结点的位置
BinaryTreeNode<T> *pointer = root; //保存输入参数
while (!aStack.empty() || pointer) { //pointer保存当前结点位置,stack中最后一个元素保存pointer的父节点位置
//因此stack为空表明 没有要回溯的父节点了, pointer为nullptr表明走到这颗子树访问完了,即全部访问完;
if (pointer) {
Visit(pointer->value()); //访问当前结点,第一次遇到就访问先序
aStack.push(pointer); //当前结点地址入栈,第一次遇到此结点 push
pointer = pointer->leftchild(); //当前链接结构指向左孩子
}
else { //左子树的左子树的左……遍历完毕,转向从遍历右子树
pointer = aStack.top(); //栈顶元素退栈
aStack.pop(); //第二次遇见此结点 pop
//Visit(pointer->value()); 第二次遇到就访问, 中序
pointer = pointer->rightchild(); //当前链接结构指向右孩子
}//endif
} //endwhile
}
template<class T>
void BinaryTree<T>::InOrderWithoutRecursion(BinaryTreeNode<T> *root) { //非递归中序周游二叉树或其子树
using std::stack; //使用STL中的stack
stack<BinaryTreeNode<T>* > aStack;
BinaryTreeNode<T> *pointer = root; //保存输入参数
while (!aStack.empty() || pointer) {//pointer保存当前结点位置,stack中最后一个元素保存pointer的父节点位置
//因此stack为空表明 没有要回溯的父节点了, pointer 为nullptr表明走到这颗子树访问完了,即全部访问完;
if (pointer) {
aStack.push(pointer); //当前结点地址入栈,第一次遇到此结点 push
pointer = pointer->leftchild(); //当前链接结构指向左孩子
}
else { //左子树访问完毕,转向访问右子树
pointer = aStack.top();
aStack.pop(); //栈顶元素退栈 第二次遇见此结点 pop
Visit(pointer->value()); //访问当前结点
pointer = pointer->rightchild(); //当前链接结构指向右孩子
}
} //endwhile
}
template<class T>
void BinaryTree<T>::PostOrderWithoutRecursion(BinaryTreeNode<T> *root) {//非递归后序周游二叉树或其子树
using std::stack; //使用STL栈部分
StackElement<T> element; //中间变量
stack<StackElement<T > > aStack; //栈申明
BinaryTreeNode<T> *pointer;
if (root == nullptr)
return; //空树即返回
else pointer = root; //保存输入参数
while (!aStack.empty() || pointer) {
while (pointer != nullptr) { //深度一直搜直到左子树的左子树……为nullptr
element.pointer = pointer; //保留当前结点信息
element.tag = Left; //标记为 左孩子
aStack.push(element); //第一次遇到此结点,push
pointer = pointer->leftchild(); //沿左子树方向向下周游
}
element = aStack.top(); //开始回溯
aStack.pop(); //托出栈顶元素,第二次遇到此结点pop()
pointer = element.pointer;
if (element.tag == Left) { //标记位位 Left 从左子树回来(是第一次回溯),接着去访问右子树
element.tag = Right; //标记为右子树
aStack.push(element); //相当于把刚才 出栈的那个元素 换一个标记
pointer = pointer->rightchild(); //同样方式遍历右孩子
}
else { //从右子树回来 ,第三次遇到此节点
Visit(pointer->value()); //第二次回溯了,可以访问当前结点了
pointer = nullptr; //以为着一颗子树已经遍历完了,可以 回溯了(如果未遍历完)
}
}
}
template<class T>
void BinaryTree<T>::LevelOrder(BinaryTreeNode<T> *root) { //借助队列采用bfs进行层序遍历
//按层次周游二叉树或其子树
using std::queue; //使用STL的队列
queue<BinaryTreeNode<T>*> aQueue;
BinaryTreeNode<T> *pointer = root; //保存输入参数
if (pointer)
aQueue.push(pointer); //根结点入队列
while (!aQueue.empty()) { //队列非空
pointer = aQueue.front(); //取队列首结点
aQueue.pop(); //当前结点出队列
Visit(pointer->value()); //访问当前结点
if (pointer->leftchild())
aQueue.push(pointer->leftchild()); //左子树进队列
if (pointer->rightchild())
aQueue.push(pointer->rightchild()); //右子树进队列
}
}
#endif /*BINARY_TREE*/
#include"Binary_tree.h"
#include<iostream>
using namespace std;
int main() {
BinaryTree<char> a, b, c, d, e, f, g, h, i, nulltree;
d.CreateTree('D', nulltree, nulltree); //从下往上一颗颗的连成一整颗树
g.CreateTree('G', nulltree, nulltree);
h.CreateTree('H', nulltree, nulltree);
i.CreateTree('I', nulltree, nulltree);
f.CreateTree('F', h, i);
e.CreateTree('E', g, nulltree);
b.CreateTree('B', d, e);
c.CreateTree('C', nulltree, f);
a.CreateTree('A', b, c); //以A为根
cout << "This tree is:\n";
cout << " A \n";
cout << " / \\ \n";
cout << " B C \n";
cout << " / \\ \\ \n";
cout << " D E F \n";
cout << " / / \\ \n";
cout << " G H I \n";
cout << endl;
//前序周游二叉树
cout << "Preorder sequence is: " << endl;
a.PreOrder(a.Root()); //递归
cout << endl;
cout << "Preorder sequence Without Recursion is: " << endl;
a.PreOrderWithoutRecursion(a.Root());//非递归
cout << endl;
//中序周游二叉树
cout << "Inorder sequence is: " << endl;
a.InOrder(a.Root()); //递归
cout << endl;
cout << "Inorder sequence Without Recursion is: " << endl;
a.InOrderWithoutRecursion(a.Root());//非递归
cout << endl;
//后序周游二叉树
cout << "Postorder sequence is: " << endl;
a.PostOrder(a.Root()); //递归
cout << endl;
cout << "Postorder sequence Without Recursion is: " << endl;
a.PostOrderWithoutRecursion(a.Root());//非递归
cout << endl;
//层序遍历
cout << "Levelorder sequence Without Recursion is: " << endl;
a.LevelOrder(a.Root());
cout << endl;
//root
cout << "Root is: " << a.Root()->value() << endl;
/* //delete tree
a.DeleteBinaryTree(a.Root());
cout<<"Tree is deleted."<<endl; //没有问题,在析构函数中调用
*/
return 0;
}
二叉树遍历的算法分析
1.时间代价
二叉树遍历算法的时间代价在各种遍历中, 每个结点都被访问且只被访问一次,时间代价为O(n)
非递归保存入出栈(或队列)时间
前序、中序,某些结点入/出栈一-次 ,不超过O(n)
后序,每个结点分别从左、右边各入/出一次, O(n)
2.空间代价
深搜:栈的深度与树的高度有关
最好O(log n)
最坏O(n)
























 3405
3405

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








