布隆过滤器
集合只有加入和查询,用较小的空间。
如:有100亿条url黑名单比较当前网站是否在其中
允许有失误,不在过滤器里面,误报成在。
创建m bit长度的数组。对每个url通过不同hash函数的值并%上m,获得k个值,在m数组上涂黑,当碰到已经涂黑的不管。
查的时候,对要查的url同样操作,对获得的值比较,如果都涂黑则一定在里面。

n为样本量,p为失误率

并行解决岛问题(并查集)
在矩阵中有每个位置和上下左右相连,如果都唯一为一个岛,求一个矩阵有多少个岛?
并查集
只提供判断是否是同一个集合,合并两个集合,两个功能。
先给出所有集合,让每个集合指向自己。
判断是否同一集合,比较两元素最高指向:顶,是否相同。
合并两个集合,让数量少的顶指向多的顶。
优化:扁平化,把所有元素都指向顶,节省查找时间
解决
把大的切除后分别并行,记录递归起始点和边界点。
一共有多少起始点有多少集合,把相邻的边界点做并查集。
kmp算法
字符串str1,str2,如果str1包含str2返回开始位置。
next数组
str2的每个字符最长前缀和后缀的长度
[a,a,b,a,a,b,s,a,a,b,a,a,b,s,t]
规定第0个为-1,第一个为0
所以每个长度为
[-1,0,1,0,1,2,3,...]
解决
str1从i开始,str2从0开始比较。
当str1为x位置时,str2为y位置时匹配不成功。
标准:str1回退到i+1,str2回退到0.
kmp:
因为,知道str2的前缀和后缀想同长度k,所以str1,x位置前k位置一定和str2前k位置相同,所以str2只需要后退到k+1比较就行。
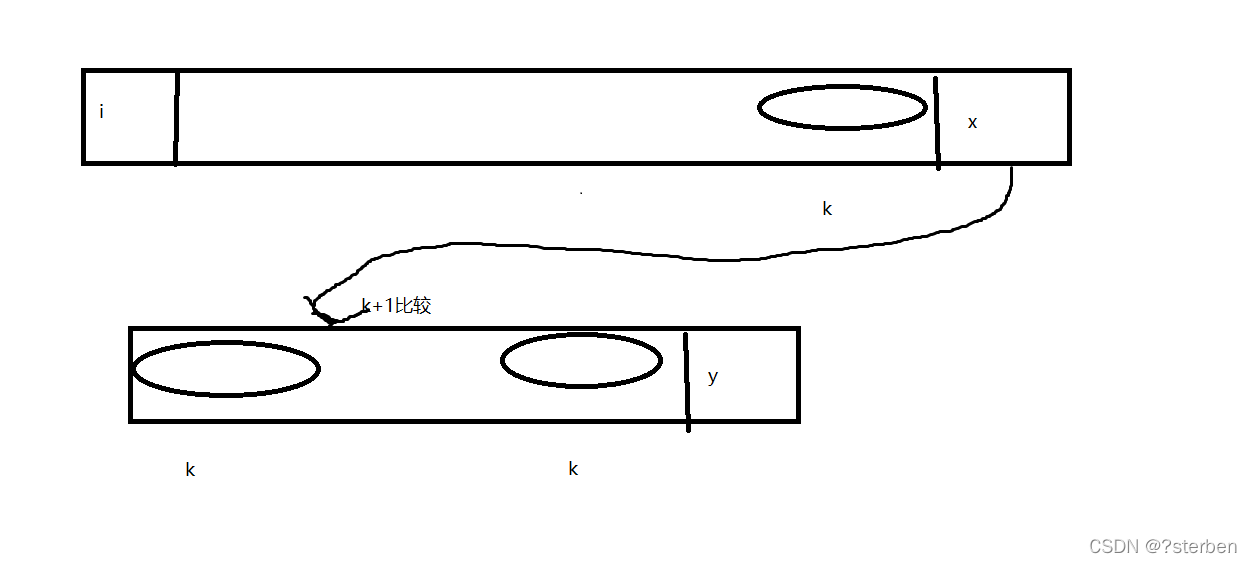
如果不等,就继续后退
next数组
求第 i 位置的最大长度
1、获得 i-1 位置的长度
2、比较 i-1 和 i-1 的最大长度的前半截的后一位 k
3、如果 k=i-1 则 i 的长度为 next[i-1]+1
4、如果不等,则利用 k 位的最大长度前半截的后一位 j 和 i-1 比较。

public static void main(String[] args) {
String str1 = "BBC ABCDAB ABCDABDABDE";
String str2 = "AB A";
int[] next = getNext(str2);
System.out.println(Arrays.toString(next));
char[] l1 = str1.toCharArray();
char[] l2 = str2.toCharArray();
// one:str1当前位置,two:str2当前位置
int one=0,two=0;
while (one<l1.length && two<l2.length){
if (l1[one] == l2[two]){
one++;
two++;
// 如果two在首位也匹配不了,则str1前进
}else if (next[two] == -1){
one++;
// two还能前跳,继续跳
}else {
two = next[two];
}
}
int star = two==l2.length?one-two:-1;
System.out.println(star);
}
// 获得next数组
public static int[] getNext(String str2){
int[] next = new int[str2.length()];
char[] array = str2.toCharArray();
next[0] = -1;
next[1] = 0;
int i = 2;
// 前一个next的长度
int c = 0;
// 全部找一遍
while (i<next.length){
// 如果前一个位置和前一个位置最大长度的后一个比较
if (array[i-1] == array[0]){
// 相等则当前位置的长度为前一个位置加一,i加一
c+=1;
next[i] = c;
i+=1;
// 如果c大于0,说明前一个还有相同的继续找
}else if (c>0){
// 把c变为前一个的前一个
c = next[c];
// 前面没有想的只有重新开始
}else {
next[i++] = 0;
}
}
return next;
}
manacher算法
求最长回文
abba
abcba
都是回文
求a121b回文
经典:
1、进行扩容:a#1#2#1#b
2、对每位进行两边对比
manachaer:
1、x 没有在最右回文范围里,暴力扩
2、x 在最右回文里,根据最右回文中心点,找到对称点 i ,对称点之前求过回文区域
2.1、对称点回文区域在最右回文区域内,那么x回文区域大小就为i的回文区域
2.2、i的回文区域超过最右回文,x回文区域长度为 最右回文-i回文
2.3、i的回文与最右回文压线,x回文一部分是i,再可以从最右回文右边开始暴力扩
String s = "acbahkafojlnavnufnavkvnv";
// String s = "abba";
String kZS = getKuoZhanS(s);
System.out.println(getPArr(s));
// 左程云老师的
System.out.println(maxLcpsLength(s));
}
// 获得扩展后的字符串
public static String getKuoZhanS(String s) {
StringBuilder sbuider = new StringBuilder();
sbuider.append("#");
for (int i = 0; i < s.length(); i++) {
sbuider.append(s.substring(i, i + 1));
sbuider.append("#");
}
return sbuider.toString();
}
public static int getPArr(String s) {
String kZS = getKuoZhanS(s);
// 每个位置的长度数组
int[] pArr = new int[kZS.length()];
// R:最大半径到达位置,C:最大半径中心,max:最大半径
int R = -1, C = -1,max=Integer.MIN_VALUE;
for (int i = 0; i < kZS.length(); i++) {
// 中心在最大半径外,暴力扩
if (i >= R) {
int l = getBLKR(kZS, i, i + 1);
pArr[i] = l;
if (l + i > R) {
R = l + i;
C = i;
}
// 中心在最大半径内
} else {
// 对于最大半径中心对称的点i`的半径在最大半径边上,除了i-pArr[dCD]-1和i+pArr[dCD]+1开始暴力扩
int dCD = 2 * C - i;
if (dCD - pArr[dCD] == C - pArr[C]) {
int l = getBLKR(kZS, i, i + pArr[dCD]) + pArr[dCD];
pArr[i] = l;
if (l + i > R) {
R = l + i;
C = i;
}
// 不需要暴力扩
}else {
pArr[i] = Math.min(R-i-pArr[dCD],pArr[dCD]);
}
}
max = Math.max(max, pArr[i]);
}
return max;
}
// 暴力扩获得半径
public static int getBLKR(String kZS, int center, int index) {
// 左边需要对比的位置
int left = center - index + center;
// 长度
int l = 0;
// 如果右边对比位置超出扩展长度,左边位置小于0
while (index < kZS.length() && left >= 0) {
if (kZS.substring(left, left + 1).equals(kZS.substring(index, index + 1))) {
index++;
l++;
} else {
break;
}
left = center - index + center;
}
return l;
}
public static int maxLcpsLength(String s) {
if (s == null && s.length() == 0) {
return 0;
}
char[] kZS = getKuoZhanS(s).toCharArray();
int[] pArr = new int[kZS.length];
int C = -1, R = -1, max = Integer.MIN_VALUE;
for (int i = 0; i < kZS.length; i++) {
pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
while (i + pArr[i] < kZS.length && i - pArr[i] > -1) {
if (kZS[i + pArr[i]] == kZS[i - pArr[i]]) {
pArr[i]++;
} else {
break;
}
}
if (i + pArr[i] > R) {
R = i + pArr[i];
C = i;
}
max = Math.max(max, pArr[i]);
}
return max - 1;
}
窗口问题
给数组长度为n,窗口大小为w,窗口每次向右滑1,求每次窗口内的最大值数组?
数组为:[4,3,5,4,3,3,6,7]
窗口大小为3
最大值数组为:[5,5,5,4,6,7]
用双端队列。求最大值则左到右,大到小
R每向右移动,把该位置的下表移动到队列中,严格按照大到小,比R位置上小的都弹出,相同也弹。再放入。
L向右动,比较前一位置的下标是不是队首,是弹出。
单调栈
求i位置左边离他最近的大的数,右边比他大离他近的数。
栈为从底到上大到小。
每次放入坐标,如果放入的数比栈顶大,则弹出。弹出时生成数据。
弹出i位置,左边离你最近的大的数为弹出下面的位置,右边最近大的数为当前位置。
如果遍历玩,栈中还有数据,则单独出栈。
如果有重复值,则把重复的下表压在一起,左边离他最近最大的为最右边的下标
树形dp套路
从二叉树的节点a出发,沿途节点只能经过一次,到达节点b是路径上的节点个数叫做a到b的距离,求整颗数的最大距离
1、x不参与
左最大距离
右最大距离
2、x参与
左高+1+右高
三者之间取最大值


Morris遍历
一种二叉树的遍历方式,时间复杂度为O(N),额外空间复杂度为O(1)。


先序遍历

中序遍历

后序遍历
第二次回到car逆序打印左树右边界,再单独逆序打印整个右边界


区间过滤
32位的无符号整数范围是0~4294967295,现有一个包含40亿个符号整数的文件,内存限制为3KB,求一个没出现过的数。
最多能够申请3KB/4 ~ 最多2的9次方512。所以可以申请int[512]数组,把2的32次方分为512份,a = 2的32次方 / 512,40亿每位都除以a,得几就把数组上该位+1,因为40亿数全部在2的32次方里,如果哪位不够a则说明在该范围内差数,在该范围再分成512份,继续过40亿数,直到精确到个。
二维堆
某搜索公司一天的用户词汇搜索是海量的,请设计出一种求出每天热门top100词汇的可行方法。
用哈希把词汇分配到不同的堆中并统计次数,再利用总堆把每个堆的头词汇放入总堆中,每次弹出头部,并在堆中删除相应词汇,再重新把该堆中的头部放入总堆。总堆持续弹出100次。
无运算符运算
给定a,b执行加减乘除会导致内存溢出,那么你给定函数不必对此负责,除此之外保证计算过程不溢出。
加
两数相加的和等于两数异或a和两数相与向左移一位b的和,用a,b继续异或和与左移,当不能与左移位时,结果就为当前异或结果。

减法
a加b的相反数

乘法

动态规划
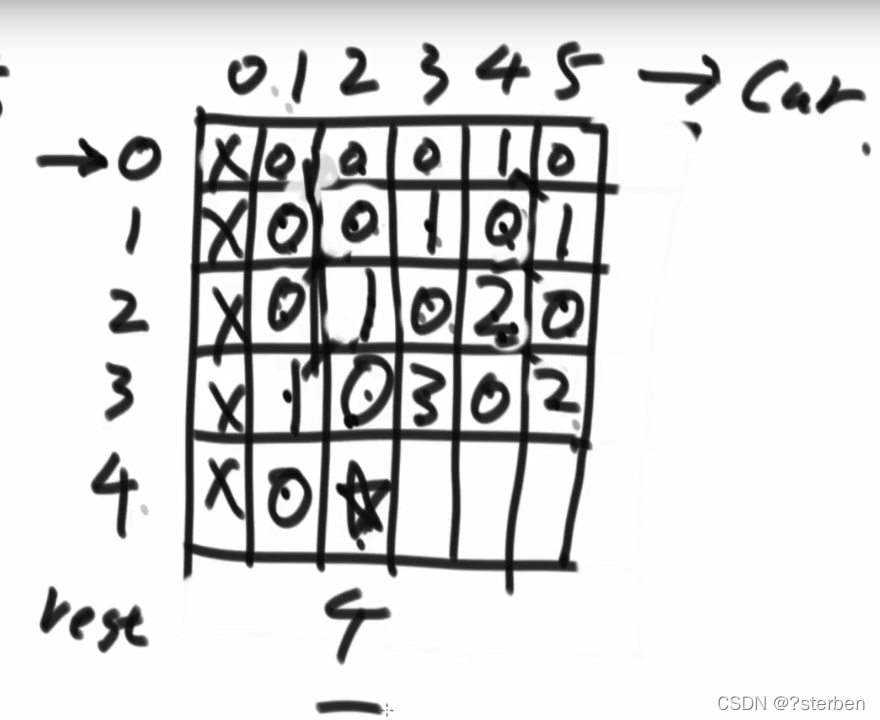
有1-N个位置,当前位置为K,要求在X步内移动到M位置,不能停止不动,求有多少步?
暴力递归

因为当后两个值确定,返回值一定确定,在暴力过程中会重复递归,可以用空间换时间

计划递归

严格表结构
下一步优化表的建立,根据动态递归的条件可以判断出当
以横坐标为当前位置,竖坐标为剩余步数的表。
当前位置为1时不可能到达0位置,当前的值为右上的值,最右边的值为左上的值,之间的值为左上+右上

AVL树
任何一个节点左右两个节点相差不超过1
利用左旋和右旋
当加入一个节点,检测从该节点往上具不具备平衡性
当删除一个节点,从顶替该节点的上一个节点开始查
SB树


平衡后谁的孩子节点变化了继续调

跳表

跳表在插入时会随机获得层数,如图要插入70,获得层数2层。
找到最右边最高层数的小于等于70的值,为20,层数为5
70没有5层,所以20降一层,最右节点变成50,再降到2层,把50第二层指向70,70指向100
找规律


等概率返回
一个函数f,可以1~5等概率返回,请加工出1-7的数字等概率返回的函数g
设定函数如果f返回的数小于3则返回0,大于3返回1,等于3重新f。
返回0-7只要3个二进制位,得到的数+1就是等概率,位7重试

函数f,可以等概率返回a-b的一个,加工出c-d的数字概率函数g
思路一样,提供13-21,返回30-59
把f加工成0和1返回器,17以下返回0以上返回1,21重试
0-29为5位二进制位,拼起来
函数f,以p概率返回0,1-p返回0,加工出等概率返回0和1的函数g
加工返回0和1,揉两回,得到【0,1】和【1,0】可以返回0或1
求有效括号
定义dp数组,dp[i]为以当前位置为尾的长度。
如果为左括号则为0,
如果为右括号则看dp[i-1]的值,往前推dp[i-1]个长度,到p位置,
如果为右括号为0
如果为左括号,则再加dp[-1]的前一个位置的值

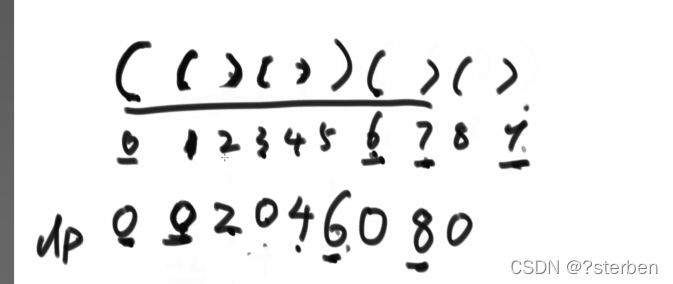
IndexTree(数组移动问题)
两种颜色的球,蓝色和红色,按1~n编号,共计2n个,为方便红球编号为负,蓝球不变,并打乱顺序。要求同一颜色的球升序排序,交换相邻两球,求最少操作次数。
[3,-3,1,-4,2,-2,-1,4] 最终交换结果为[1,2,3,-1,-2,-3,-4,4] 最少交换为10次
伪代码
/**
* @param lasta 最后蓝色球的数
* @param lastb 最后红色球的数
* @param arr 原始数组
* @return
*/
public static int zuo(int lasta,int lastb, int[] arr){
//蓝色和红色的球数都为0,说明排序已经全部完成
if (lasta==0 && lastb==0){
return 0;
}
//lasta已经全部移动完毕
if (lasta==0){
int curCost = lastb来到此时最后位置的代价;
int next = zuo(lasta, lastb-1, arr);
return curCost+next;
}
//lastb已经全部移动完毕
if (lastb==0){
int curCost = lasta来到此时最后位置的代价;
int next = zuo(lasta-1, lastb, arr);
return curCost+next;
}
//都没有,中间位置
int p1=Integer.MAX_VALUE,p2=Integer.MAX_VALUE;
//lasta来到最后
int lastaComeHost = lasta来到此时最后位置的代价;
int next1 = zuo(lasta-1, lastb, arr);
p1 = lastaComeHost+next1;
//lastb来到最后
int lastbComeHost = lastb来到此时最后位置的代价;
int next2 = zuo(lasta-1, lastb, arr);
p2 = lastbComeHost+next2;
return Math.min(p1,p2);
}
计算来到当前位置的代价利用indexTree
indextree为数组长度的全为1的数组。
计算从x位置到y位置的代价,即计算x~y位置1的个数减1:2到4代价为3-1 = 2。并把2设为0.
这样原数组不用改变。之前改变1为0,计算1个数时已经变了。
例如:
【2,1,-3,-1】 最后位置为3,indextree为【1,1,1,1】
第一轮: 2到3 【2,1,-1,-3】 移动 sum(2 ~ 3) - 1 = 1 indextree【1,1,0,1】
第二轮: 3到2 【2,1,-1,-3】 移动 sum(3 ~ 2)-1 = 0 indextree 【1,1,0,0】
第三轮: 0到1 【1,2,-1,-3】 移动 sum(0 ~ 1) -1 = 1 indextree 【0,1,0,0】
同理 一共移动2步 ,不用移动数组只要改变indextree即可
public static int zuo(int lasta, int lastb,
IndexTree it, //支持快速查找距离
int end, // 不变永远 n-1
HashMap<Integer,Integer> map // 位置表
){
//蓝色和红色的球数都为0,说明排序已经全部完成
if (lasta==0 && lastb==0){
return 0;
}
int p1=Integer.MAX_VALUE,p2=Integer.MAX_VALUE;
int index,cost,next;
if (lastb!=0){
index = map.get(lastb);
cost = it.sum(index,end)-1;
it.add(index,-1);
next = zuo(lasta, lastb-1, it, end-1, map);
it.add(index,1);
p1=cost+next;
}
if (lasta!=0){
index = map.get(lasta);
cost = it.sum(index,end)-1;
it.add(index,-1);
next = zuo(lasta-1, lastb, it, end-1, map);
it.add(index,1);
p2=cost+next;
}
return Math.min(p1,p2);
}
只有lasta和lastb变换可以改成动态规划
位图
int set=0
表示32位
set |= 1 << 0
表示把第0位变成一
除法向上取整(a+b-1)/b
计算有几个1
1、Integer.bitCount(set)
2、循环检查二进制位
int ret = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) {
ret++;
}
}
return ret;
3、位运算优化
int ret = 0;
while (n != 0) {
n &= n - 1;
ret++;
}
return ret;

//names : 用户数组。查询shiyans:实验数组
public void zuo(int[][] names, int[][] shiyans) {
int n = names.length, m = shiyans.length;
//创建位图每个实验有n人
int[][] sets = new int[m][(n + 31) / 32];
//遍历用户数组修改sets位图,建立m号实验每个对应n个人位图
for (int i = 0; i < n; i++) {
for (int j : names[i]) {
sets[j][i / 32] |= 1 << (i % 32);
}
}
int[] ans = new int[shiyans.length];
//每次查询
for (int i=0;i<shiyans.length;i++){
//一次查询的实验集合第一次查{1,2,3}实验人数
int[] shiyan = shiyans[i];
int count = 0;
//把每个实验的位图取出来进行|运算求1,每个实验有(n+31)/32位
for (int j=0;j<(n+31)/32;j++){
int set=0;
//第k个实验
for (int k : shiyan) {
// |运算上第k个实验的第j位:j=0 0-31位同学有多少
set |= sets[k][j];
}
//统计(k*32) ~ (k+1)*32-1 个去重同学有多少
count+=Integer.bitCount(set);
}
ans[i] = count;
}
}
差分数组
有n位数组,设:n=4:[0,0,0,0]
有f操作f[i] = [1,3,2]:1到3位加2:[2.2.2.0]
求每位的数字和。
可以用差分数组,添加第0位和n+1位数组: [0,0,0,0,0,0]
执行1到3位加时,第一位加,第m+1位-。即:[0,2,0,0,-2,0]
统计是结果为前一位累加和:[0,2+0,2+0,2+0,0 (-2+2),0]


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








