在深度强化学习(Deep Reinforcement Learning, DRL)的收敛图中,横坐标选择 steps 或者 episodes 主要取决于算法的设计和实验的需求,两者的差异和使用场景如下:
- Steps(步数):
- 定义:一个 step 通常指的是在环境中执行一次动作并收到一次反馈(即状态转移和奖励)。因此,
steps代表的是智能体与环境交互的总次数。 - 使用场景:当我们关心算法每一步(action)如何影响学习效果,或想评估算法在更细粒度时间尺度下的学习过程时,常用
steps作为横坐标。对于一些环境来说,steps可以更好地反映学习的进展,尤其是当每个 episode 的长度不固定或差异较大时,steps会提供更一致的度量。 - 如果不同回合的 episode 长度差异较大(如某些游戏中早期失败快、后期成功时间长),用 step 能更均匀地展示进度,避免单个长回合掩盖细节。
- 适用算法:比如在一些连续控制任务中,steps 更有意义,因为这些任务中的 episode 可能较长或很难明确划分。
- 定义:一个 step 通常指的是在环境中执行一次动作并收到一次反馈(即状态转移和奖励)。因此,
# time: 2025/2/21 12:47
# author: YanJP
# 以下是一个基于DQN算法的完整示例代码,横坐标为训练步数(step),每一步交互后更新网络。示例使用CartPole环境,并展示如何以step为横坐标绘制收敛曲线。
import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import collections
import random
import matplotlib.pyplot as plt
# 配置参数
ENV_NAME = "CartPole-v1"
STATE_DIM = 4
ACTION_DIM = 2
BUFFER_CAPACITY = 10000
BATCH_SIZE = 128
LR = 1e-3
GAMMA = 0.99
TAU = 0.005 # 目标网络软更新参数
TOTAL_STEPS = 30000 # 总训练步数
EPS_START = 1.0
EPS_END = 0.01
EPS_DECAY = 2000 # epsilon衰减步数
# 定义DQN网络
class DQN(nn.Module):
def __init__(self):
super().__init__()
self.net = nn.Sequential(
nn.Linear(STATE_DIM, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, ACTION_DIM)
)
def forward(self, x):
return self.net(x)
# 经验回放缓冲区
class ReplayBuffer:
def __init__(self):
self.buffer = collections.deque(maxlen=BUFFER_CAPACITY)
def push(self, transition):
self.buffer.append(transition)
def sample(self):
return random.sample(self.buffer, BATCH_SIZE)
def __len__(self):
return len(self.buffer)
# 初始化组件
env = gym.make(ENV_NAME)
policy_net = DQN()
target_net = DQN()
target_net.load_state_dict(policy_net.state_dict())
optimizer = optim.Adam(policy_net.parameters(), lr=LR)
buffer = ReplayBuffer()
# 训练记录
step_rewards = []
total_rewards = []
episode_reward = 0
episode_num = 0
# 在变量初始化部分添加
steps_per_episode = [] # 用于存储每个episode的长度(step数)
episode_steps = 0 # 追踪当前episode已进行多少step
# 训练主循环
state = env.reset()
epsilon = EPS_START
for step in range(1, TOTAL_STEPS + 1):
# 1. 执行动作 (epsilon-greedy)
if random.random() < epsilon:
action = env.action_space.sample()
else:
action= policy_net(torch.FloatTensor(state)).argmax().item()
episode_steps += 1 # 新增:每次step后累加
# 2. 与环境交互,获得下一个状态和奖励
next_state, reward, done, _ = env.step(action)
# 记录当前episode的累计奖励
episode_reward += reward
# 3. 存储经验到回放缓冲区
buffer.push((state, action, reward, next_state, done))
# 转移到下一个状态
state = next_state
# 4. 如果episode结束,重置环境
if done:
state = env.reset()
steps_per_episode.append(episode_steps) # 记录该episode的总step数
episode_steps = 0 # 重置计数器
total_rewards.append(episode_reward)
# total_rewards.append(episode_reward)
episode_reward = 0
episode_num += 1
# 5. epsilon线性衰减
epsilon = EPS_END + (EPS_START - EPS_END) * np.exp(-1. * step / EPS_DECAY)
# 6. 训练步骤(当缓冲区数据足够时)
if len(buffer) >= BATCH_SIZE:
# 从缓冲区采样一批数据
batch = buffer.sample()
state_b, action_b, reward_b, next_state_b, done_b = zip(*batch)
# 转换为PyTorch张量
state_b = torch.FloatTensor(np.array(state_b))
action_b = torch.LongTensor(action_b).unsqueeze(1) # 保持维度一致
reward_b = torch.FloatTensor(reward_b)
next_state_b = torch.FloatTensor(np.array(next_state_b))
done_b = torch.BoolTensor(done_b) # 用于mask终止状态
# 计算当前Q值 (Q(s,a))
q_current = policy_net(state_b).gather(1, action_b)
# 计算目标Q值 (r + γ * max Q_target(s', a')
with torch.no_grad(): # 目标网络不需要梯度
q_next = target_net(next_state_b).max(1)[0] # 取最大值
q_target = reward_b + GAMMA * q_next * (~done_b) # done时q_target=reward
# 计算损失(均方误差)
loss = nn.MSELoss()(q_current.squeeze(), q_target)
# 反向传播优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录每一步的损失和奖励(可选)
step_rewards.append(reward)
# 7. 目标网络软更新(按TAU比例混合参数)
for target_param, policy_param in zip(target_net.parameters(), policy_net.parameters()):
target_param.data.copy_(TAU * policy_param.data + (1 - TAU) * target_param.data)
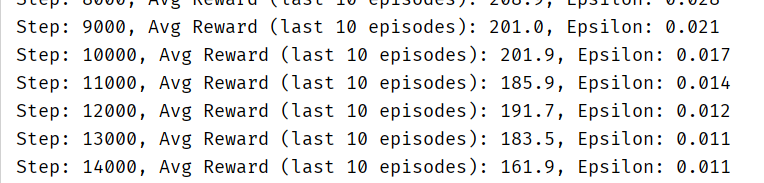
# 每1000步打印训练进展
if step % 1000 == 0:
avg_reward = np.mean(total_rewards[-10:]) if len(total_rewards) >= 10 else np.mean(total_rewards)
print(f"Step: {step}, Avg Reward (last 10 episodes): {avg_reward:.1f}, Epsilon: {epsilon:.3f}")
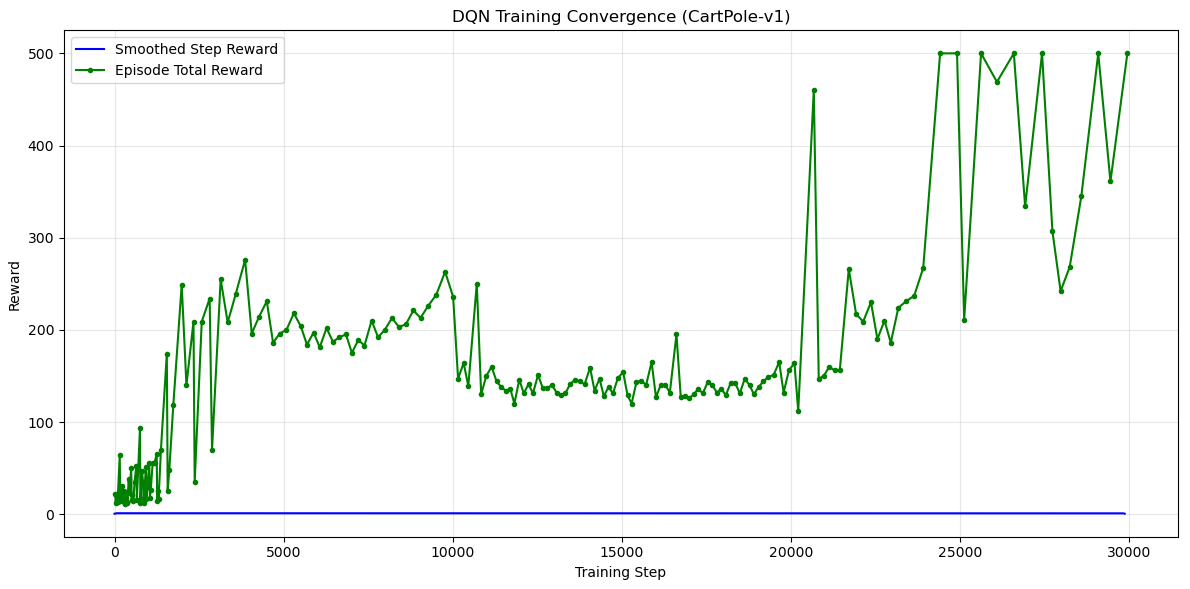
# 修改后的画图部分代码
plt.figure(figsize=(12, 6))
# 1. 平滑的step奖励曲线
window_size = 100
# 使用 'same' 模式,使得输出长度与输入相同,通过填充处理两端
smoothed_step_rewards = np.convolve(step_rewards, np.ones(window_size)/window_size, mode='same')
plt.plot(range(len(step_rewards)), smoothed_step_rewards, label='Smoothed Step Reward', color='blue')
# # 或者,使用 'valid' 模式并调整横坐标
# smoothed_step_rewards = np.convolve(step_rewards, np.ones(window_size)/window_size, mode='valid')
# x = np.arange(window_size // 2, len(step_rewards) - window_size // 2 + 1)
# plt.plot(x, smoothed_step_rewards, label='Smoothed Step Reward', color='blue')
# 2. 每个episode的总奖励(仅在完成episode时绘制)
if len(total_rewards) > 0:
# 累积每个episode的step数得到在总step中的位置
# 需要额外定义steps_per_episode变量记录每个episode的步数
ep_steps = np.cumsum(steps_per_episode) # 正确的累积方式
plt.plot(ep_steps, total_rewards, 'o-', markersize=3, label='Episode Total Reward', color='green')
plt.xlabel("Training Step")
plt.ylabel("Reward")
plt.title("DQN Training Convergence (CartPole-v1)")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
- Episodes(回合):
- 定义:一个 episode 是智能体从环境的初始状态开始执行动作,直到到达终止状态(例如游戏结束、目标达成、或者智能体失败等)。一个 episode 包含了多个 steps。
- 使用场景:当我们关心智能体在整个任务中的表现变化时,
episodes作为横坐标更常见。通常,用于表示算法在完成完整任务(例如游戏、导航等)过程中逐渐收敛的情况,适合于那些有明确开始和结束的任务。 - 适用算法:例如在基于离散动作空间的任务(如游戏、迷宫导航等)中,episodes 更容易反映智能体在每次尝试完成任务时的表现。
- 适用于需整个回合结束后才能更新的算法(如蒙特卡洛方法、REINFORCE)。这类算法依赖于完整的奖励轨迹进行统计,因此用 episode 自然贴合其更新逻辑。
# time: 2025/2/22 11:28
# author: YanJP
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
import gym
# -------------------
# 神经网络模型定义
# -------------------
class DQN(nn.Module):
def __init__(self, input_dim, output_dim):
super(DQN, self).__init__()
self.net = nn.Sequential(
nn.Linear(input_dim, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU(),
nn.Linear(128, output_dim)
)
def forward(self, x):
return self.net(x)
# -------------------
# 经验回放缓冲区
# -------------------
class ReplayBuffer:
def __init__(self, capacity):
self.capacity = capacity
self.buffer = []
self.position = 0
def push(self, state, action, reward, next_state, done):
if len(self.buffer) < self.capacity:
self.buffer.append(None)
self.buffer[self.position] = (state, action, reward, next_state, done)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
indices = np.random.choice(len(self.buffer), batch_size, replace=False)
states, actions, rewards, next_states, dones = zip(*[self.buffer[i] for i in indices])
return (
torch.FloatTensor(np.array(states)),
torch.LongTensor(np.array(actions)),
torch.FloatTensor(np.array(rewards)),
torch.FloatTensor(np.array(next_states)),
torch.FloatTensor(np.array(dones))
)
def __len__(self):
return len(self.buffer)
# -------------------
# 训练参数设置
# -------------------
env = gym.make('CartPole-v1')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
model = DQN(state_dim, action_dim)
target_model = DQN(state_dim, action_dim)
target_model.load_state_dict(model.state_dict())
optimizer = optim.Adam(model.parameters(), lr=1e-3)
buffer = ReplayBuffer(10000)
batch_size = 64
gamma = 0.99
epsilon = 1.0
epsilon_min = 0.01
epsilon_decay = 0.995
# -------------------
# 训练循环 (以Episode为中心)
# -------------------
total_episodes = 200
episode_rewards = [] # 核心: 记录每个episode的总奖励
smoothed_episode_rewards = []
for episode in range(total_episodes):
state = env.reset()
episode_reward = 0
done = False
while not done:
# ε-greedy策略选择动作
if np.random.rand() < epsilon:
action = env.action_space.sample()
else:
with torch.no_grad():
q_values = model(torch.FloatTensor(state))
action = q_values.argmax().item()
# 与环境交互
next_state, reward, done, _ = env.step(action)
episode_reward += reward
# 存储经验
buffer.push(state, action, reward, next_state, done)
state = next_state
# 从回放缓冲区学习
if len(buffer) >= batch_size:
states, actions, rewards, next_states, dones = buffer.sample(batch_size)
# 计算Q值
current_q = model(states).gather(1, actions.unsqueeze(1))
next_q = target_model(next_states).max(1)[0].detach()
target_q = rewards + gamma * next_q * (1 - dones)
# 计算损失
loss = nn.MSELoss()(current_q.squeeze(), target_q)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 更新目标网络
if episode % 10 == 0:
target_model.load_state_dict(model.state_dict())
# ε衰减
epsilon = max(epsilon_min, epsilon * epsilon_decay)
# 记录当前episode的奖励
episode_rewards.append(episode_reward)
# 计算滑动平均奖励(窗口大小=20)
window_size = 20
if len(episode_rewards) >= window_size:
avg_reward = np.mean(episode_rewards[-window_size:])
smoothed_episode_rewards.append(avg_reward)
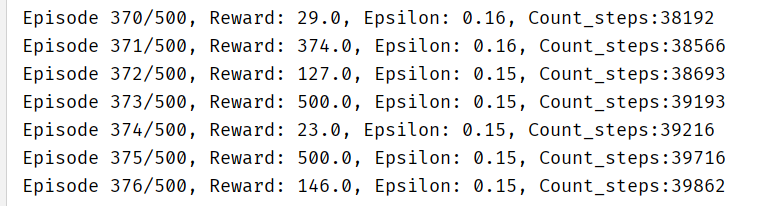
# 打印进度
print(f"Episode {episode + 1}/{total_episodes}, Reward: {episode_reward}, Epsilon: {epsilon:.2f}")
# -------------------
# 可视化结果 (横坐标为Episode)
# -------------------
plt.figure(figsize=(12, 6))
# 绘制原始Episode奖励
episodes = np.arange(1, len(episode_rewards) + 1)
plt.plot(episodes, episode_rewards, 'o', markersize=3, alpha=0.5, label='Raw Episode Reward')
# 绘制平滑后的曲线(对齐EPISODE坐标)
if len(smoothed_episode_rewards) > 0:
smooth_episodes = np.arange(window_size, len(episode_rewards) + 1)
plt.plot(smooth_episodes, smoothed_episode_rewards,
linewidth=2, label=f'Smoothed (window={window_size})', color='orange')
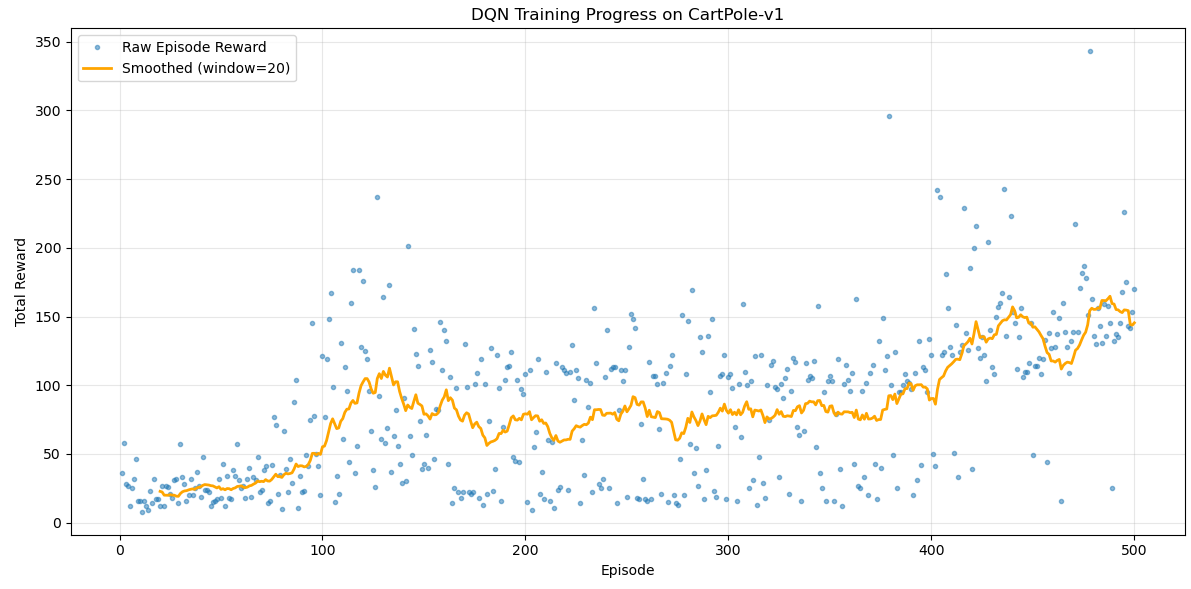
plt.xlabel("Episode")
plt.ylabel("Total Reward")
plt.title("DQN Training Progress on CartPole-v1")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
选择依据:
- 任务的结构:如果任务有明确的回合(例如一个游戏关卡),那么使用
episodes更直观。如果任务没有明显的回合,或者回合长度变化较大,steps可能是更好的选择。 - 评估目标:如果你想观察智能体在每一个决策点的学习情况,用
steps可能更合适;如果你更关注智能体在整个任务(回合)中的学习进展,episodes会更合理。 - 算法特点:一些算法可能对每步的细粒度表现(如
steps)更加敏感,而另一些算法则关注整体表现(如episodes)。
简而言之,steps 适用于精细粒度的分析,episodes 适用于较高层次的任务表现分析。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








