本文深入解析了ConcurrentHashMap的内部结构，重点讲解了分段锁Segment的高效并发控制、哈希冲突的链表处理和树化策略，以及关键方法如put、rehash和size()的实现原理。同时揭示了如何通过自旋锁、线程迁移和负载均衡优化并发性能。
目录
2. Segment -> scanAndLockForPut()
1.7
特点
- 使用分段锁 Segment，继承自 ReentrantLock；只对某一段进行加锁，不会进行全局加锁；锁之间互不影响，提高并行度。
- Segment 内部为 HashEntry 数组，等同于 HashMap 内部结构。
- 发生哈希冲突，连接成链表，采用头插法。
https://mp.weixin.qq.com/s?__biz=MzkyMjIzOTQ3NA==&mid=2247484633&idx=1&sn=87cb3d1f0670f598e4c6b72f0e188132&source=41#wechat_redirect
初始化
1. 重要属性
// 默认 map 大小，即 HashEntry 的默认数量 static final int DEFAULT_INITIAL_CAPACITY = 16; // 默认负载因子 static final float DEFAULT_LOAD_FACTOR = 0.75f; // 默认并行度，即 segment 数组大小(分段锁数量) static final int DEFAULT_CONCURRENCY_LEVEL = 16; // 最大容量 static final int MAXIMUM_CAPACITY = 1 << 30; // 每个分段最小容量，即最少 HashEntry 数量 static final int MIN_SEGMENT_TABLE_CAPACITY = 2; // 每个分段最大容量 static final int MAX_SEGMENTS = 1 << 16; // slightly conservative // 默认自旋次数，当自旋次数超过此值，则阻塞等待锁释放； // 避免执行 size() 时，map 被频繁更新，导致无限进行自旋，影响性能 static final int RETRIES_BEFORE_LOCK = 2; // 用于索引 segment 的掩码值，key 哈希值的高位用于选择 segment final int segmentMask; // 用于索引 segment 时，使用的偏移值，以此得到 key 哈希值的高位 final int segmentShift; // Segment 数组 final Segment<K,V>[] segments;
2. 构造方法
// initialCapacity HashEntry 的数量； // loadFactor 负载因子； // concurrencyLevel 并行度(segment 数量，分段锁数量) public ConcurrentHashMap(int initialCapacity, float loadFactor, int concurrencyLevel) { if (!(loadFactor > 0) || initialCapacity < 0 || concurrencyLevel <= 0) throw new IllegalArgumentException(); if (concurrencyLevel > MAX_SEGMENTS) concurrencyLevel = MAX_SEGMENTS; // 幂次 int sshift = 0; // 并行度(segment 数量，分段锁数量)，为 2 ^ sshift int ssize = 1; while (ssize < concurrencyLevel) { ++sshift; ssize <<= 1; } // 索引 segment 时，使用的偏移值； // 右移 segmentShift 位，得到 key 哈希值高 sshift 位 this.segmentShift = 32 - sshift; // 索引 segment时，使用的掩码 this.segmentMask = ssize - 1; if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; int c = initialCapacity / ssize; if (c * ssize < initialCapacity) ++c; // 每个 segment 里，HashEntry 的数量； // 等于，大于 initialCapacity / ssize 的，2 的幂次 int cap = MIN_SEGMENT_TABLE_CAPACITY; while (cap < c) cap <<= 1; // 创建第一个 segment；其他均为懒加载，并以 segments[0] 为模板 Segment<K,V> s0 = new Segment<K,V>(loadFactor, (int)(cap * loadFactor), (HashEntry<K,V>[])new HashEntry[cap]); // 初始化 segments Segment<K,V>[] ss = (Segment<K,V>[])new Segment[ssize]; // 保证可见性 UNSAFE.putOrderedObject(ss, SBASE, s0); // ordered write of segments[0] this.segments = ss; }
3.Segment 内重要属性
// scanAndLockForPut中自旋循环获取锁的最大自旋次数 static final int MAX_SCAN_RETRIES = Runtime.getRuntime().availableProcessors() > 1 ? 64 : 1; // 键值对，存储结构 transient volatile HashEntry<K,V>[] table; // 实际键值对个数；无 volatile 修饰，不保证可见性 transient int count; // segment元素修改次数记录 transient int modCount; // 扩容阈值 transient int threshold; // 负载因子 final float loadFactor;
4.HashEntry 内重要属性
final int hash; final K key; // 确保可见性 volatile V value; // 确保可见性 volatile HashEntry<K,V> next;
get()
// 没有加锁操作，弱一致性换取性能 public V get(Object key) { Segment<K,V> s; // manually integrate access methods to reduce overhead HashEntry<K,V>[] tab; // 获取 key 对应的 hash 值 int h = hash(key); // 通过 hash 值高位计算得到 Segment 的偏移量 long u = (((h >>> segmentShift) & segmentMask) << SSHIFT) + SBASE; // 使用 volatile 读，获取对应的 Segment if ((s = (Segment<K,V>)UNSAFE.getObjectVolatile(segments, u)) != null && // HashEntry[] 不为空 (tab = s.table) != null) { // 1. 通过 hash 值低位计算得到 HashEntry 的偏移量； // 2. 使用 volatile 读，获取 HashEntry 的链表头结点；进行遍历 // 3. happens-before 原则：①volatile 写在读之前 ②解锁在加锁之前 // 4. 即使第一时间获取到的是新值，但是并发环境下，可能刚获取完，就被更新了 // (先读后写了)；弱一致性，体现在这 for (HashEntry<K,V> e = (HashEntry<K,V>) UNSAFE.getObjectVolatile (tab, ((long)(((tab.length - 1) & h)) << TSHIFT) + TBASE); e != null; e = e.next) { K k; if ((k = e.key) == key || (e.hash == h && key.equals(k))) return e.value; } } return null; }没有加锁操作，弱一致性换取性能
put()
1. Segment -> put()
final V put(K key, int hash, V value, boolean onlyIfAbsent) { // 尝试获取锁，获取成功则 node = null； // 获取失败，则进入 scanAndLockForPut 方法，自旋获取锁 HashEntry<K,V> node = tryLock() ? null : scanAndLockForPut(key, hash, value); // 因为加了锁，同一时刻都只有一个线程执行下面的操作； // 并且解锁前，数据都会同步到主存，所以无需使用 volatile 修饰变量； // 减小 volatile 对性能的影响 V oldValue; try { HashEntry<K,V>[] tab = table; int index = (tab.length - 1) & hash; // --- 标记 --- HashEntry<K,V> first = entryAt(tab, index); for (HashEntry<K,V> e = first;;) { if (e != null) { K k; if ((k = e.key) == key || (e.hash == hash && key.equals(k))) { oldValue = e.value; if (!onlyIfAbsent) { e.value = value; ++modCount; } break; } e = e.next; } else { // 表示其他线程在自旋过程中，已经创建了新结点； // 得到锁时，不需要再创建一遍，减少了锁的占用时间 if (node != null) // 将 node 使用头插法 node.setNext(first); else node = new HashEntry<K,V>(hash, key, value, first); // 先判断是否扩容，再插入新结点； // HashMap 是先插入，再判断扩容，可能导致扩容后再无新结点插入； // 造成无效扩容 int c = count + 1; if (c > threshold && tab.length < MAXIMUM_CAPACITY) // 已经加锁，确保扩容安全 rehash(node); else // --- 标记 --- setEntryAt(tab, index, node); ++modCount; count = c; oldValue = null; break; } } } finally { // 解锁 unlock(); } return oldValue; }
2. Segment -> scanAndLockForPut()
private HashEntry<K,V> scanAndLockForPut(K key, int hash, V value) { HashEntry<K,V> first = entryForHash(this, hash); HashEntry<K,V> e = first; HashEntry<K,V> node = null; int retries = -1; // negative while locating node // 获取锁失败，则遍历链表，将遍历过的 HashEntry 放入 CPU 高速缓存中； // 获取锁之后，再次定位速度会十分快，等待过程中的一种预热方式 while (!tryLock()) { HashEntry<K,V> f; // to recheck first below // 首次进入，retries = -1 恒成立 if (retries < 0) { // e = null 的原因：①HashEntry[] 对应位置为 null②遍历表到最后，没有指定 key if (e == null) { // 再次进入循环，避免重复符值 if (node == null) // speculatively create node node = new HashEntry<K,V>(hash, key, value, null); retries = 0; } // 找到指定 key else if (key.equals(e.key)) retries = 0; else e = e.next; } // 自旋次数超过最大次数，则直接进入阻塞； // 无限制的自旋，性能损耗比阻塞更大 else if (++retries > MAX_SCAN_RETRIES) { lock(); break; } // 遍历过程中，发现链表已经被改变，则重新进行遍历 else if ((retries & 1) == 0 && (f = entryForHash(this, hash)) != first) { e = first = f; // re-traverse if entry changed retries = -1; } } return node; }
rehash()
private void rehash(HashEntry<K,V> node) { HashEntry<K,V>[] oldTable = table; int oldCapacity = oldTable.length; int newCapacity = oldCapacity << 1; threshold = (int)(newCapacity * loadFactor); HashEntry<K,V>[] newTable = (HashEntry<K,V>[]) new HashEntry[newCapacity]; // 新掩码，比原来的多一位 1；00001111 -> 00011111 int sizeMask = newCapacity - 1; for (int i = 0; i < oldCapacity ; i++) { HashEntry<K,V> e = oldTable[i]; if (e != null) { HashEntry<K,V> next = e.next; // 生成新下标 int idx = e.hash & sizeMask; // 没有后继节点，只有单个节点 if (next == null) // Single node on list // 新数组可以直接引用 newTable[idx] = e; else { // 非单节点 // Reuse consecutive sequence at same slot HashEntry<K,V> lastRun = e; int lastIdx = idx; for (HashEntry<K,V> last = next; last != null; last = last.next) { int k = last.hash & sizeMask; if (k != lastIdx) { lastIdx = k; // 第一个后续所有节点在新数组中下标保持不变的节点 lastRun lastRun = last; } } //这个for循环就是找到第一个后续节点新的index不变的节点。 newTable[lastIdx] = lastRun; // Clone remaining nodes //lastRun 之前的结点均需复制一遍 for (HashEntry<K,V> p = e; p != lastRun; p = p.next) { int h = p.hash; // 生成新下标 int k = h & sizeMask; // 头插法 HashEntry<K,V> n = newTable[k]; newTable[k] = new HashEntry<K,V>(h, p.key, p.value, n); } } } } // 为新加入的节点，在新数组生成下标 int nodeIndex = node.hash & sizeMask; // add the new node // 头插法 node.setNext(newTable[nodeIndex]); // 新数组下标指向新节点 newTable[nodeIndex] = node; // 赋值给原数组 table = newTable; }
- put 时，会判断 Segment 里的 HashEntry 数量是否超过阈值(threshold)；超过则进行扩容。
- rehash() 是没有加锁的，因为外层已经加了锁，确保是单线程操作。
- 过程：新建容量为原来两倍的新数组；每个桶，找到第一个后续所有节点在新数组中下标保持不变的节点 lastRun，新数组可直接引用 lastRun，之前的结点全部需要复制。
size()
public int size() { final Segment<K,V>[] segments = this.segments; // HashEntry 数量 int size; // 是否溢出 boolean overflow; // 本次的 modcount 值 long sum; // 上次的 modcount 值 long last = 0L; int retries = -1; // first iteration isn't retry try { for (;;) { // 当 retries = RETRIES_BEFORE_LOCK 时，全部 Segment 加锁 // 会导致本来延迟加载的 Segment 全部创建 if (retries++ == RETRIES_BEFORE_LOCK) { for (int j = 0; j < segments.length; ++j) // ensureSegment 确保该 Segment 已经创建； // segments[0] 为模板，懒加载其他结点 ensureSegment(j).lock(); // force creation } sum = 0L; size = 0; overflow = false; for (int j = 0; j < segments.length; ++j) { Segment<K,V> seg = segmentAt(segments, j); if (seg != null) { // 本轮 modcount sum += seg.modCount; // 本 Segment 元素数量 int c = seg.count; if (c < 0 || (size += c) < 0) overflow = true; } } // modcount 没变，则计算结果准确 if (sum == last) break; last = sum; } } finally { // 只有当 retries = RETRIES_BEFORE_LOCK 时，才加锁；防止未加锁，进行解锁 if (retries > RETRIES_BEFORE_LOCK) { for (int j = 0; j < segments.length; ++j) segmentAt(segments, j).unlock(); } } return overflow ? Integer.MAX_VALUE : size; }
1.8
特点
- 使用 synchronized + CAS 保证并发安全。
- 发生哈希冲突，链表 + 红黑树。
- 扩容时，多个线程分摊进行，提高效率（多核）。
重要属性
// 最大容量 static final int MAXIMUM_CAPACITY = 1 << 30; // 默认容量 static final int DEFAULT_CAPACITY = 16; // 负载因子 private static final float LOAD_FACTOR = 0.75f; // 树化阈值 static final int TREEIFY_THRESHOLD = 8; // 树退化阈值 static final int UNTREEIFY_THRESHOLD = 6; // 树化最低节点数量要求 static final int MIN_TREEIFY_CAPACITY = 64; // 各线程最低迁移桶的数量 private static final int MIN_TRANSFER_STRIDE = 16; // 最大帮助线程数量 static final int MAX_RESIZERS = (1 << (32 - RESIZE_STAMP_BITS)) - 1; // 起始扩容线程标志 static final int RESIZE_STAMP_SHIFT = 32 - RESIZE_STAMP_BITS; // 已经完成迁移的桶的标志 static final int MOVED = -1; // CPU 核数 static final int NCPU = Runtime.getRuntime().availableProcessors(); // 当前节点数量 transient volatile long baseCount; // 扩容阈值 transient volatile int sizeCtl; // 下一个需要迁移的区间的起始位置 transient volatile int transferIndex; // 计数单元表，用于合并计算总的结点数 transient volatile CounterCell[] counterCells;
addCount()
// 真正 put 进新元素之后，需要执行的操作。 private final void addCount(long x, int check) { //⭐减少自旋对性能的损耗： // 1.1 所有线程都尝试修改 baseCount，可能会导致大量的自旋； // 1.2 将修改操作分散：线程对应 CounterCell[] 中一个元素，进行修改，减少自旋； // 1.3 最后的 sumCount() 是将 CounterCell[] 所有结果相加，得到最终结果。 CounterCell[] as; long b, s; if ((as = counterCells) != null || !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) { CounterCell a; long v; int m; boolean uncontended = true; if (as == null || (m = as.length - 1) < 0 || (a = as[ThreadLocalRandom.getProbe() & m]) == null || !(uncontended = U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) { fullAddCount(x, uncontended); return; } if (check <= 1) return; s = sumCount(); } // 检查是否需要扩容 if (check >= 0) { Node<K,V>[] tab, nt; int n, sc; // 此时 sizeCtl 还是代表阈值； // 扩容开始后会变成负值，依旧成立； // ⭐重要作用：线程迁移完自己所负责的区域之后，发现扩容还在进行，则继续帮助扩容 while (s >= (long)(sc = sizeCtl) && (tab = table) != null && (n = tab.length) < MAXIMUM_CAPACITY) { int rs = resizeStamp(n); // sizeCtl < 0 表示扩容正在进行中 if (sc < 0) { // 判断扩容是否完成，扩容线程是否达到上限 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; // 加入扩容，扩容线程数 + 1 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } // 扩容还未开始，当前线程开启扩容，初始化新数组 // (rs << RESIZE_STAMP_SHIFT) + 2) 为特定值，用于判断是否为第一个线程 // CAS 操作确保只有一个线程开启扩容 else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); // 获取最终结果 s = sumCount(); } } }
tryPresize()
treeifyBin() -> tryPresize()：真正树化前，需要判断当前节点总数。
putAll() -> tryPresize()：批量添加前，会检查是否需要扩容。
// 1. 批量插入，调用该方法。 // 2. 链表节点数 >= 8，但是节点总数 < 64，调用该方法。 private final void tryPresize(int size) { int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY : tableSizeFor(size + (size >>> 1) + 1); int sc; // 为负数，表示在初始化或扩容 while ((sc = sizeCtl) >= 0) { Node<K,V>[] tab = table; int n; // 数组还未初始化 if (tab == null || (n = tab.length) == 0) { n = (sc > c) ? sc : c; // 初始化时，sizeCtl 设为 -1。 if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { try { if (table == tab) { Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; table = nt; // 阈值只占真实容量的 3/4。 sc = n - (n >>> 2); } } finally { sizeCtl = sc; } } } else if (c <= sc || n >= MAXIMUM_CAPACITY) break; // 判断扩容 else if (tab == table) { int rs = resizeStamp(n); . //---- 与 addCount() 相同的扩容判断。 . } } }
helpTransfer()
扩容时，调用插入、删除、合并等修改操作，遇到 ForwardingNode 节点（hash = -1），该线程会进行帮助扩容。
final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) { Node<K,V>[] nextTab; int sc; if (tab != null && (f instanceof ForwardingNode) && (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null) { int rs = resizeStamp(tab.length); //⭐重要作用：线程迁移完自己所负责的区域之后，发现扩容还在进行，则继续帮助扩容 while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0) { // 判断扩容是否完成或者线程已经达到上限。 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || transferIndex <= 0) break; // 加入扩容。 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) { transfer(tab, nextTab); break; } } return nextTab; } return table; }
transfer
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) { int n = tab.length, stride; // stride：每个线程负责多少个桶。 // 单核则负责全部桶，每个线程至少负责 16 个桶。 if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; // 第一个线程开启扩容，初始化新数组。 if (nextTab == null) { try { Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1]; nextTab = nt; } catch (Throwable ex) { sizeCtl = Integer.MAX_VALUE; return; } nextTable = nextTab; transferIndex = n; } int nextn = nextTab.length; // 新建一个占位节点，放在桶的首部; // 1.该桶已经迁移完毕，整体还处于扩容状态。 // 2.当执行 get() 时，转发至新数组。 ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab); // 单纯用作循环条件，循环内部计算下一个桶的位置。 boolean advance = true; // 代表整个迁移工作是否完成。 boolean finishing = false; // bound：线程负责区域左边界；为长度为 stride 区间的左边界。 // nextIndex：线程负责区域右边界；为长度为 stride 区间的右边界。 for (int i = 0, bound = 0;;) { Node<K,V> f; int fh; while (advance) { int nextIndex, nextBound; // 每次处理完一个桶，i 就左移 if (--i >= bound || finishing) advance = false; // 分配的起始位置 <= 0，表示扩容已经完成 else if ((nextIndex = transferIndex) <= 0) { i = -1; advance = false; } // 首次进入循环，计算出分配区域 else if (U.compareAndSwapInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { // 当前线程处理区域的左边界 bound = nextBound; // 当前线程开始处理的下标位置 i = nextIndex - 1; advance = false; } } // 当前线程负责区域已经迁移完成 if (i < 0 || i >= n || i + n >= nextn) { int sc; // 整体扩容结束 if (finishing) { nextTable = null; table = nextTab; // 更新阈值 sizeCtl = (n << 1) - (n >>> 1); return; } // 扩容线程数量 - 1 if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { // 当前线程是否为最后一个线程 if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return; finishing = advance = true; // 重新遍历所有桶，以防遗漏 i = n; // recheck before commit } } // 当前桶为空，插入占位节点 else if ((f = tabAt(tab, i)) == null) advance = casTabAt(tab, i, null, fwd); // 当前桶已经迁移完成 else if ((fh = f.hash) == MOVED) advance = true; else { synchronized (f) { if (tabAt(tab, i) == f) { Node<K,V> ln, hn; if (fh >= 0) { int runBit = fh & n; // 确定最后一个位发生变化的 key Node<K,V> lastRun = f; for (Node<K,V> p = f.next; p != null; p = p.next) { int b = p.hash & n; if (b != runBit) { runBit = b; lastRun = p; } } if (runBit == 0) { ln = lastRun; hn = null; } else { hn = lastRun; ln = null; } for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; // 采取头插法，lastRun 在后面 if ((ph & n) == 0) ln = new Node<K,V>(ph, pk, pv, ln); else hn = new Node<K,V>(ph, pk, pv, hn); } setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } // 链表式遍历，最后判断是否需要树化 else if (f instanceof TreeBin) { TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> lo = null, loTail = null; TreeNode<K,V> hi = null, hiTail = null; int lc = 0, hc = 0; for (Node<K,V> e = t.first; e != null; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode<K,V> (h, e.key, e.val, null, null); if ((h & n) == 0) { if ((p.prev = loTail) == null) lo = p; else loTail.next = p; loTail = p; ++lc; } else { if ((p.prev = hiTail) == null) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t; hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t; setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true; } } } } } }过程简述：
- 计算每个线程负责迁移的桶的数量。
- 初始化新数组，新建占位节点。
- 计算出当前线程负责的具体区域。
- 开始将每个桶的元素迁移至新数组。
- 迁移当前区域完成，迁移下一个区域。
- 整体迁移完成，再从后往前扫描一遍，查看是有遗漏。
- 对于获取，没有加锁，不会阻塞。
- 对于更新，每个桶开始迁移前需要加锁，更新操作也都需要加锁，会阻塞。
迁移设计：
- 某些 key 高位为 1，扩容后可以发挥用处；hash & n = 1 的 key 在新数组中位置为 n + i；与 hash & (n ^ 2 - 1) 相等，该位置正确。
- 采用头插法；利用高位链与低位链，将桶中 key 分开；使用 lastRun 确定最后一个位置发生变化的 key（从它开始，后面的 key 都处于高位或低位），这些 key 可以不再复制；极端情况整条链都处于同位，全部无需复制。
- 红黑树采用链表式遍历，执行相同操作，最后再判断是否树化。
扫一扫
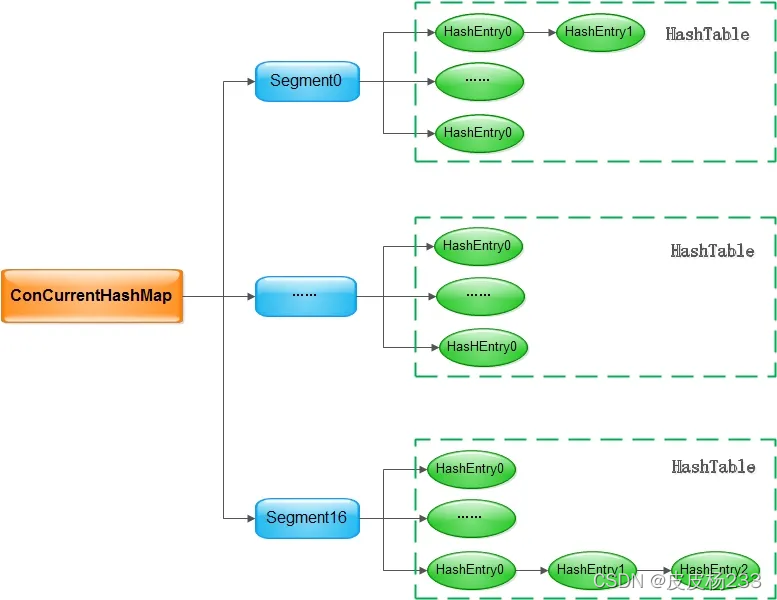
467
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
