二叉树详解-优快云博客

基本知识

定义
树是n(n >= 0)个结点的有限集合。n = 0时称为空树。在任意一棵非空树：

有且仅有一个特定的称为根的结点；
当n > 1时，其余结点可分为m(m > 0)个互不相交的有限集T1 、T2 、 … 、Tm，其中每一个集合本身又是一棵树，并且称为子树。

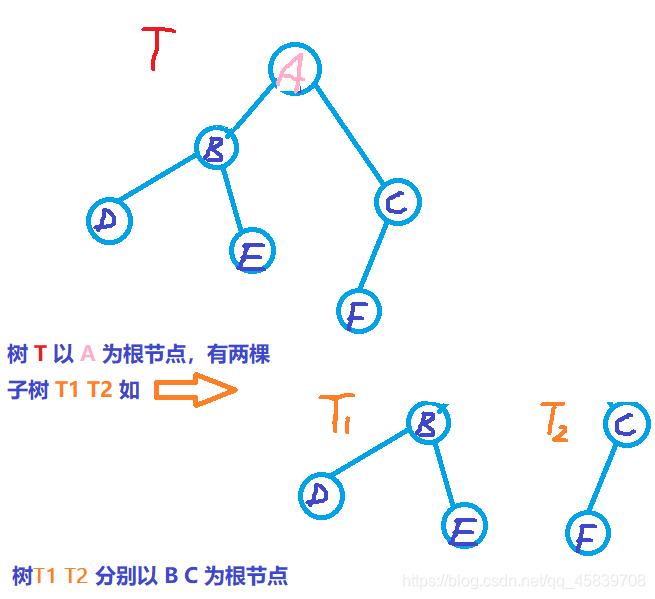
补充：
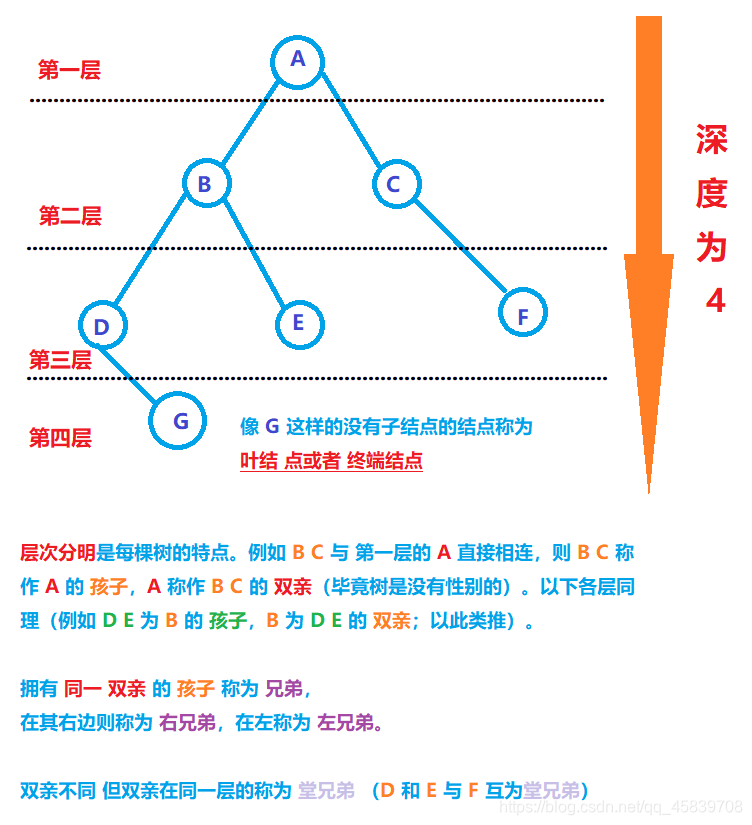
1.某个（或多个）结点它的子结点数量最多，则这个数量称作这棵树的度；
2.一棵树的层数称作此树的深度或高度

重要类型：二叉树

1.一般的树双亲结点下可以连很多子结点，但是二叉树最多连接两个子结点
2.二叉树左右子树顺序是不能颠倒的，画的时候不能都放在同一侧
3.由于第2点，即使只有一颗子树，都能很清楚的知道它是左子树还是右子树

斜树
二叉树完全往一个方向斜（只有左孩子或者右孩子），且每一层只有一个结点，结点数 = 层数 = 深度
如：
在这里插入图片描述
满二叉树
所有叶结点存在于同一层，且除了这些叶结点外，其他结点都存在左右子树
如：

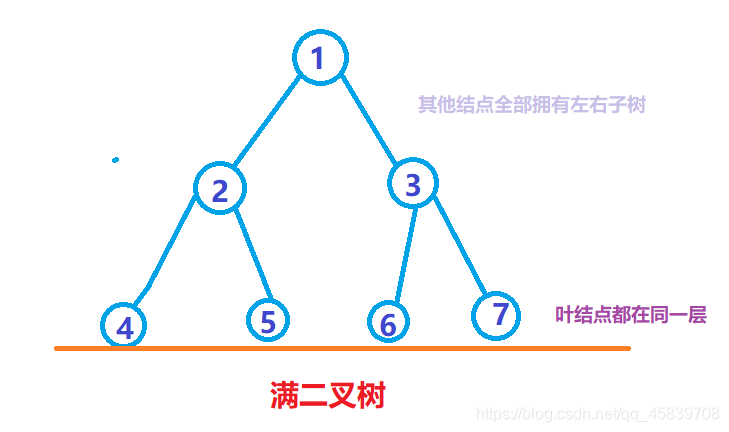
给上面结点编号是为了引出下面这种二叉树
完全二叉树
有 n 个结点的二叉树按层次序编号（一层一层来，每层从左到右），如 （4 个结点的 1 ~ 4），与 同样深度 的 满二叉树 中 编号为 i 的 结点位置完全相同，则次二叉树为完全二叉树
如：
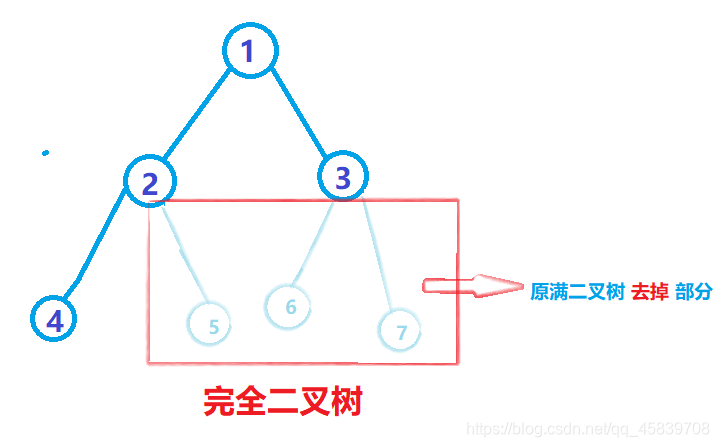
在这里插入图片描述
可以很明显的看出：完全二叉树可以由满二叉树去掉一部分得来。

1. 满二叉树一定是完全二叉树
2. 完全二叉树不一定是满二叉树
3. 可以理解成满二叉树是一种特殊的完全二叉树

二叉树性质
1 在二叉树第 i 层上至多有 2 ^i - 1 个结点（i >= 1）
2 深度为 k 的二叉树至多有 2 ^ k - 1 个结点（k >= 1）
3 任何一颗二叉树 T ，如果其终端结点数为 n0，度为 2 的结点数为 n2 则 n0 = n2 + 1
4 具有 n 个结点的完全二叉树的 深度为【log2 n】 + 1 （【x】表示不大于 x 的最大整数）

二叉树的建立与存储
递归方法更好
一般是这样出现要求你建立：

ABC##DE#G##F###

struct node
{
	int data;
	struct node*l;
	struct node*r;	
};

struct node*creat()
{
	struct node*head;
	int ch = a[i++];
	
	head = (struct node*)malloc(sizeof(struct node));
		
	if(ch == '#') // 一个字符一个字符输入，#则表示该结点为空
	{
		head = NULL;
	}
	else
	{
		head -> data = ch; // 不为空则存储数据
		head -> l = creat();
		head -> r = creat();
	}
	
	return head;
}

二叉树的遍历
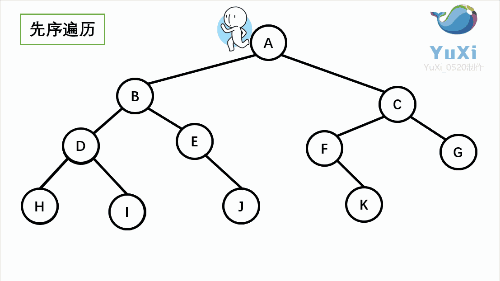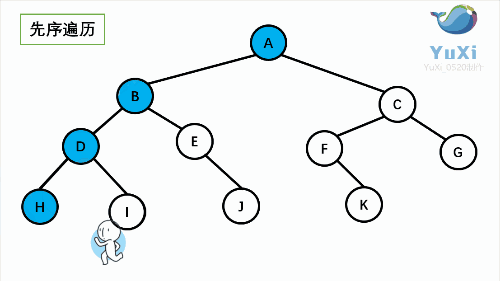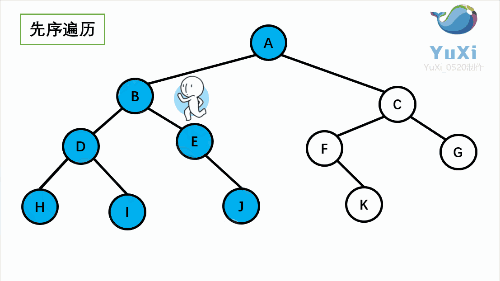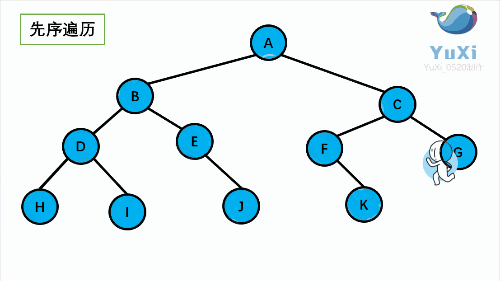
1.先序遍历（根左右）从根到 左子树 再到 右子树
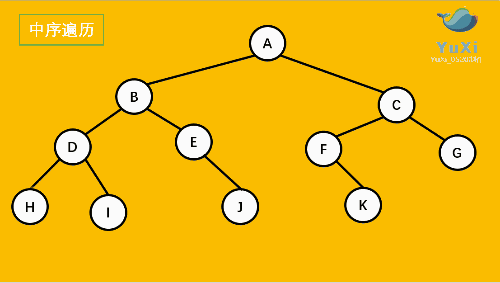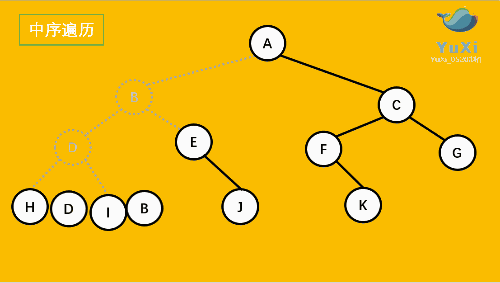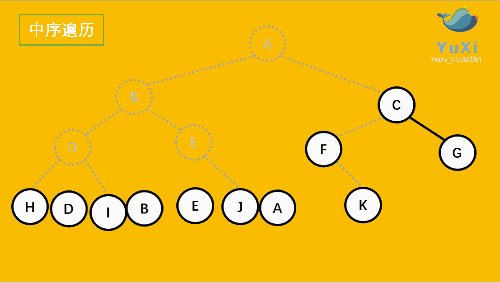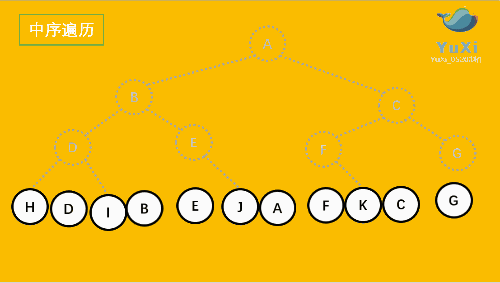
2.中序遍历（左根右）从 左子树 到根再到 右子树
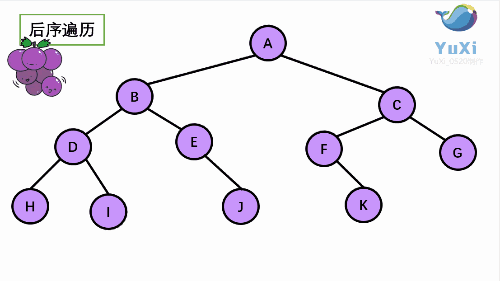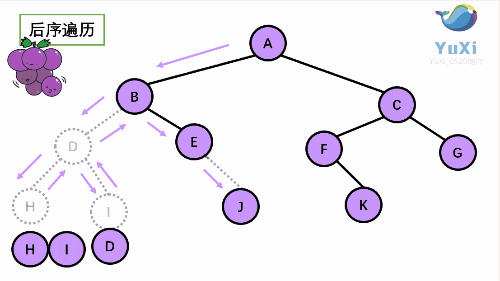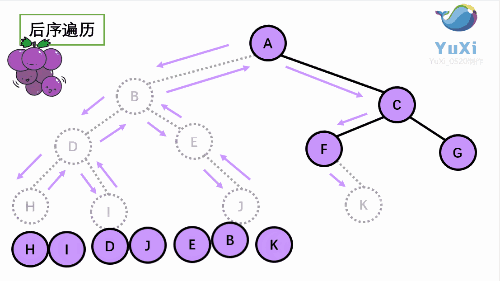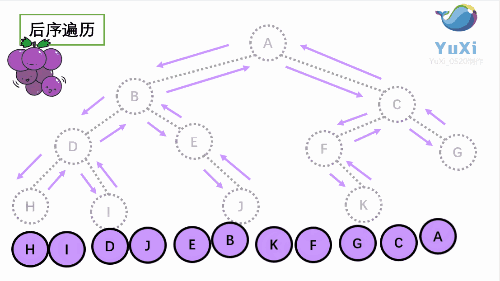
3.后序遍历（左右根）从 左子树 到 右子树 再到根

先序：
在这里插入图片描述

void printx(struct node*head)
{
	if(head == NULL)
	{
		return;
	}
	
	printf("%c",head -> data);
	printx(head -> l);
	printx(head -> r);
	return;
}

中序：
在这里插入图片描述

void printz(struct node*head)
{
	if(head == NULL)
	{
		return;
	}
	
	printx(head -> l);
	printf("%c",head -> data);
	printx(head -> r);
	return;
}

后序：
在这里插入图片描述

void printh(struct node*head)
{
	if(head == NULL)
	{
		return;
	}
	
	printx(head -> l);
	printx(head -> r);
	printf("%c",head -> data);
	return;
}

遍历图片来源于http://www.pianshen.com/article/7106254596/侵删

可以很清楚的看到，前序中序后序 完全只是 输出的位置不同，而且符合其顺序规律。

4.层次序：最简单的遍历方法，一层一层来，每层都按从左到右

void printc(struct node*head)
{
	if(head == NULL)
	{
		return;
	}
	
	queue<struct node*>dl;
	struct node*front;
	dl.push(head);
	
	while(!dl.empty())
	{
		front = dl.front();
		dl.pop();
		
		if(front -> l)dl.push(front -> l);
		if(front -> r)dl.push(front -> r);
		printf("%c",front -> data);
	}
	return;
}