二叉堆学习总结

二叉堆是一种特殊的堆，二叉堆是完全二元树（二叉树）或者是近似完全二元树（二叉树）。二叉堆有两种：最大堆和最小堆。
最大堆：父结点的键值总是 >=(大于或等于) 任何一个子节点的键值。
最小堆：父结点的键值总是 <=(小于或等于) 任何一个子节点的键值。

二叉堆用数组存储，从下标1开始，并且因为二叉堆为完全二叉树，所以除根节点外的任意节点 i 的父节点为 i / 2，除终端节点外
任意节点 i 的 左孩子为 i / 2，右孩子为 i / 2 + 1（存在右孩子时）。

接下来的一系列二叉堆操作皆以最大堆为基础

插入

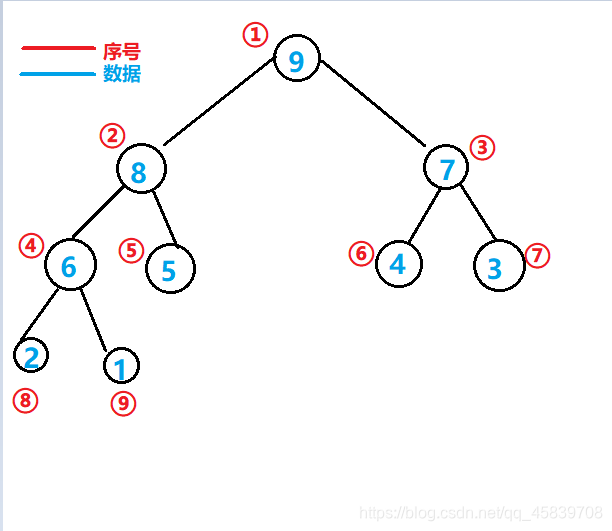
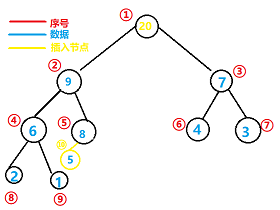
例如插入新结点，数据为 20，首先插入到数组末尾（这个末尾也代表序号 ⑤ 的左孩子）如下：

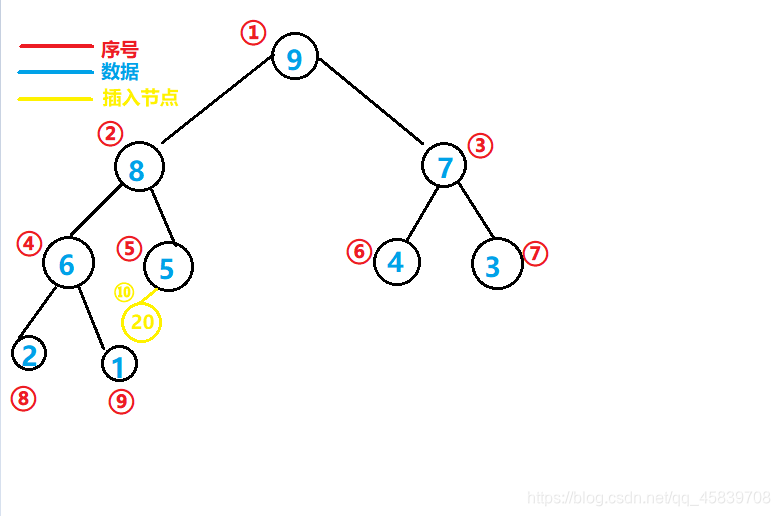
我们可以清楚的看到 新结点的加入，其数据比他的，使得原最大堆已经不符合最大堆的条件
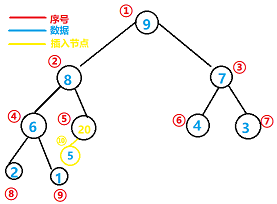
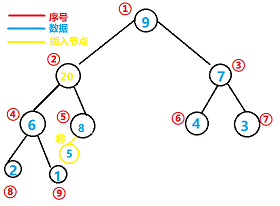
所以插入之后：
1.首先将他的数据与其父节点数据进行比较
2.假如大于的话，则进行数据交换，直到满足最大二叉堆条件如下图：

代码实现：

void insert_(int tail) // tail 指插入到尾部的新结点 
{
	int tem, father = tail / 2, son = tail;  //完全二叉树,父节点为孩子结点下标除以2 
	while(father)
	{
		if(a[father] >= a[son])
			return;
		
		if(a[father] < a[son])
		{
			tem = a[father];
			a[father] = a[son];
			a[son] = tem;
		}
		
		son = father;
		father = son / 2;  //完全二叉树,父节点为孩子结点下标除以2 
	}
	return;
}

因为二叉堆为完全二叉树，而完全二叉树的深度为 log n，所以插入操作时间复杂度为 O(log n)。

访问 / 删除

访问操作一般与删除操作是一起的

1. 访问则直接访问下标
2. 删除就直接将该结点后面所有结点的前移将其覆盖

代码实现：

int visit_delet(int adress, int end) // adress 表示访问结点的下标,end 表示末尾结点下标 
{
	int i;
	
	for(i = adress; i <= end - 1; i++)
		a[i] = a[i + 1];
	
	end--;
	
	return a[adress];
} 

访问的时间复杂度为 O(1)，删除的时间复杂度为 O(n)。

堆排序

无论是插入还是访问删除，基础都是要最初的二叉堆是符合条件的，所有堆排序在操作前是非常有必要的。
① 建立最大堆
② 将堆顶元素与末尾元素交换位置（将堆顶取出），将剩下的元素重新建立最大堆
③ 重复 ②，直到排序完成

代码实现：

void swap(int *x, int *y)
{
	int t;
	
	t = *x;
	*x = *y;
	*y = *t;
}

void percdown(int a[], int num, int root)
{
	int father, son;
	int x = a[root];
	
	for(father = root; father <= num; father = son)
	{
		son = i * 2;
		
		if(son != num && a[son + 1] > a[son]) // 判断左右结点谁更大 
			son++;
		
		if(a[son] <= x) // 取大的与根节点比较 
			break;
		else
			a[father] = a[son];
	}
	a[father] = x;
}

void head_sort(int a[], int n)
{
	int i;
	
	for(i = n / 2; i >= 1; i--) // 建立最初的最大堆 
		percdown(a, n, i);
		
	for(i = n - 1; i >= 1; i--)
	{
		swap(a[1], a[n]); // 交换堆顶与末尾元素 
		
		percdown(a, i, 0); // 将剩下元素重新建立最大堆，此时根节点应为0 
	}
}

时间复杂度 O(n logn)
适用于如：
① 10000个数中 找最小的 100个数
② 医院排队，急症优先级高，尽管可能比普通病人来得晚，但它依然能最快的到就诊。