回文串--

回文串

---

题目描述

洛谷P3649

---

回文树

回文树 (EER Tree，Palindromic Tree，也被称为回文自动机）是一种可以存储一个串中所有回文子串的高效数据结构，使用回文树可以简单高效地解决一系列涉及回文串的问题。

回文树大概长这样：

回文树是由转移边和后缀链接 (fail 指针）组成，每个节点都可以代表一个回文子串。

因为回文串长度分为奇数和偶数，因此我们需要建立两棵树，一棵树中的节点对应的回文子串长度均为奇数，另一棵树中的节点对应的回文子串长度均为偶数。也就是说，这棵回文树其实包含了两棵树。树中一个节点的 fail 指针指向的是这个节点所代表的回文串的最长回文后缀所对应的节点，但是转移边并非代表在原节点代表的回文串后加一个字符，而是表示在原节点代表的回文串前后各加一个相同的字符（不难理解，因为要保证存的是回文串）。

我们还需要在每个节点上维护此节点对应回文子串的长度 len，这个信息保证了我们可以轻松地构造出回文树。

回文树有两个初始状态，分别代表长度为-1，0的回文串。我们可以称它们为奇根，偶根，其中偶根节点是0，奇根节点是1。它们不表示任何实际的字符串，仅作为初始状态存在，这与其他自动机的根节点是异曲同工的。

特殊规定：偶根的 fail 指针指向奇根，也就是fail[0]=1。而我们并不关心奇根的 fail 指针，因为奇根不可能失配，因为奇根不代表任何实际的字符串，那么从奇根转移出去得到的是一个单字符，对于一个单字符来说，它自身本来就是回文串，因此不可能失配。

回文串的性质：比如"bcdcb"是一个回文串，那么我们在前后两端各加上一个字符a，得到的新字符串"abcdcba"仍然是一个回文串。

先给出以下变量的定义：

len[i]:表示编号为i的这个节点所表示的回文串的长度
ch[i][c]:表示在编号为i的节点所表示的回文串前后两端加上字符c后所形成的新的回文串,这个新的回文串可以用一个节点来表示 也就是ch[i][c] ch[i][c]也就是新的回文串所对应的状态节点
fail[i]:表示节点i失配后应该跳转到不等于自身的最长回文后缀所对应的节点
cnt[i]:表示节点i所表示的回文串的出现次数
last:表示上一个插入字符所在的节点
tot:表示这个回文树中添加的节点个数(不包括奇根和偶根) 我们用tot=0来表示了$字符,因此tot是从1开始来表示题目中输入的字符的
sz:表示这个回文数中的节点总数(包括奇根和偶根) 初始化时sz=-1,然后规定sz=0表示偶根 sz=1表示奇根,最终sz=tot+1

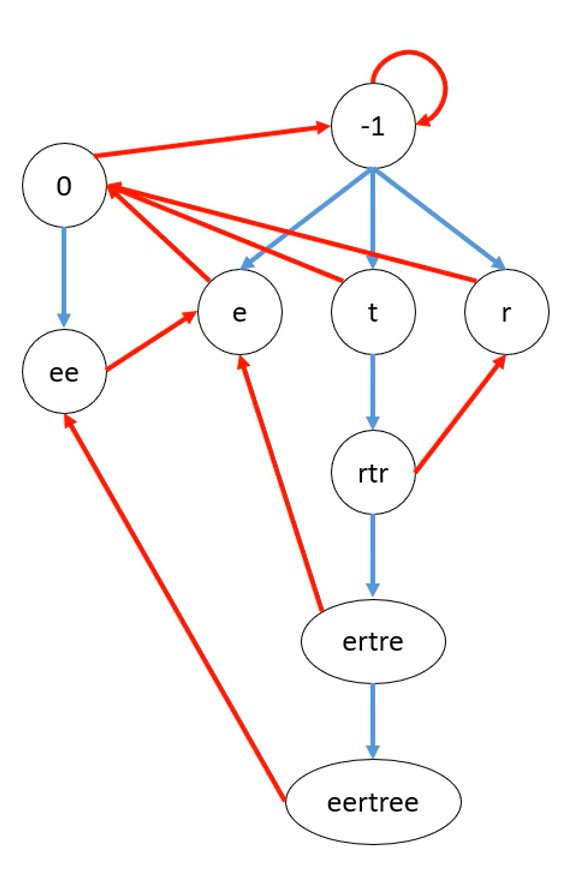
下面我们来看一下字符串"eertree"这个回文树是怎么被建造出来的：

图中的蓝边表示转移边，红边就是表示后缀链接fail指针。

图中的0表示偶根的回文长度，规定偶根的节点为0；-1表示奇根的回文长度，规定奇根的节点为1。那为什么从奇根转移出去得到的一个字符呢？首先，我们是在前后两端加上同 一个字符，那么转移后的节点长度就增加了2。由于是从奇根转移出去，因此-1+2=1，也就是1个字符。比如图中的字符e，t，r。本来是增长了两个字符ee，tt，rr，但是由于是奇根，长度为-1，因此+2后得到1，于是我们认为从奇根转移出去的得到的字符是e，t，r而不是ee，tt，rr。这也就是为什么从奇根转移出去得到的是一个单字符。

规定偶根0的fail指针指向奇根 ，奇根的fail指针指向其自身：

但是要注意明确定义了$fail[0]=1$，但是没有明确定义$fail[1]$，不过它使用的全局变量，因此默认$fail[1]=0$ 注意不是$fail[1]=1$哦

插入第一个字符E：

规定：单个字符的fail指针指向的是偶根0

接下来插入第二个字符E：

为什么ee不是从前面已经得到e连出来的呢？而是从偶根0连出来的呢？因为如果从e连出来，那么在其前后两端添加字符e，则会得到eee，而不是我们想要的ee；如果我们从偶根0连出来，由于偶根0不代表任何实际字符串，那么在其前后两端添加字符e，则会得到ee，符合我们的预期。因此是从偶根0转移出来的。

那么我们来思考一下为什么ee的fail指针会指向e呢？根据fail指针的含义可知，我们要找当前串中最长的回文后缀，对于ee来说，其后缀只有一个e，对于单个字符肯定是回文的，于是ee的最长回文后缀就是e，因此ee的fail指针指向了e，即图中ee指向e的红色边。

接下来插入第三个字符R

由于此时EER并不是回文串，因此插入的这单个字符R它是从奇根转移过来的（图中奇根到r的蓝边），而且我们规定了单个字符的fail指向的是偶根0（图中r到偶根0的红边）

接下来插入第四个字符T

由于此时EERT并不是回文串，因此插入的这单个字符T它是从奇根转移过来的（图中奇根到t的蓝边），而且我们规定了单个字符的fail指向的是偶根0（图中t到偶根0的红边）

接下来插入第五个字符R：

此时字符串为EERTR，我们发现RTR是回文串，而且它是在字符T前后两端添加字符R后转移得到的，因此从t到rtr有一条蓝边。然后我们来看RTR的fail指针该怎么求呢？RTR它的后缀有R，TR，明显TR不是回文的，而单个字符R一定是回文的，因此RTR的最长回文后缀就是R，于是从RTR到R有一条红边，即fail指针。

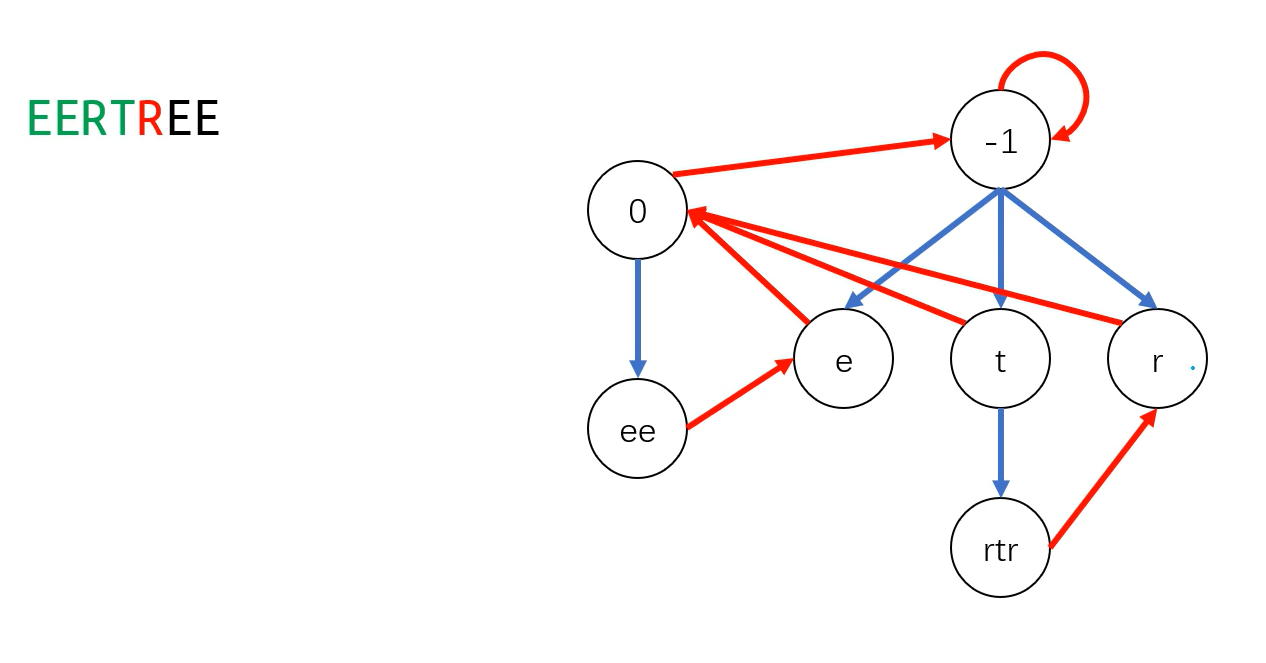
接下来插入第六个字符E：

此时字符串为EERTRE，我们发现ERTRE是回文串，而且它是在RTR前后两端添加字符E后转移得到的，因此从rtr到eertre有一条蓝边。然后我们来看ERTRE的fail指针该怎么求呢？ERTRE的后缀有E，RE，TRE，RERE，显然RE，TRE，RERE都不是回文的，而单个字符E一定是回文的，因此ERTRE的最长回文后缀就是E，于是从ERTRE到E有一条红边，即fail指针。

最后插入第七个字符E：

此时字符串为EEREREE，它就是一个回文串，而且它是在ERTRE的前后两端添加字符E后转移得到的，因此从ERTRE到EEREREE有一条蓝边。然后我们来看EEREREE的fail指针该怎么求呢？EEREREE的后缀有E，EE，REE，EREE，REREE，EREREE，从中发现EE的最长的回文后缀，于是从EEREREE到EE有一条红边，即fail指针。

引理1：向S末尾添加一个字符，最多只会新生成一个回文子串。

这里得到的新的回文子串其实是S的最长回文后缀末端增加c，且原来的前端也恰好是c，所产生的。如下图直观感受一下：

引理2：设节点$u$的回文长度为$len[u]$，任何一个满足$len[u]>1$的节点$u$的入度为1（注意这里的入度是对于蓝色的转移边来说的，而不考虑红色的fail指针的后缀链接边）

从上面的构造图中，我们可以发现：

• 如果$len[u]=1$，则其唯一的入边必然是奇根$\to u$，例如上图中的节点e，节点t，节点r，回文长度都为1，而且都是从奇根引出的蓝边
• 如果$len[u]=2$，则其唯一的入边必然是偶根$\to u$，例如上图中的节点ee，是从偶根引出的蓝边
• 如果$len[u]\ge 3$，则其唯一的入边必然为$v\to u$，满足：节点$v$所表示的回文串T的前后两端添加某个字符c后，使得节点$u$表示的回文串S满足S=cTc。例如上图中的节点rtr，其回文长度为3，它是从节点t前面两端添加字符r后转移得到的。

下面主要讲解这段代码是啥意思：

void insert(char c) //建树
{
    s[++tot] = c;
    //设此时得到的回文后缀所对应的节点是now  设其回文后缀是Q
    int now = getfail(last);
    if (!ch[now][c - 'a'])
    {
        //在回文后缀前后两端添加字符c后 得到回文串cQc 对应的状态节点是x 同时其回文长度是len[now] + 2
        int x = node(len[now] + 2);
        //注意下面的这两个顺序不能相反

        //找到x的fail指针应该连向的节点是哪个  那么我们就顺着now的fail指针走 直到不能走为止
        fail[x] = ch[getfail(fail[now])][c - 'a'];
        ch[now][c - 'a'] = x;
    }
    last = ch[now][c - 'a'];    //将当前节点ch[now][c - 'a']给last  更新last
    cnt[last]++;    //last状态节点所表示的回文串的出现次数+1
}

比如上述栗子中，现在插入第一个字符E，那么s[1]=E，last=0，执行getfail(0)，由图可知0是偶根节点，它的fail指向的是奇根1，因此经过getfail(0)后返回的结果是1，所以此时now=1，指向的是奇根节点。然后由图可知，此时奇根now还没有存在E这个节点，那么我们就创建出这个节点E，len[now]+2=len[1]+2=-1+2=1，因此经过node(1)后，返回的结果是2，即x=2，也就是说新建出来的这个节点E的编号是2。然后我们就要处理E节点它的fail指针应该指向哪个节点呢？此时fail[now]=fail[1]，而我们知道fail[1]使用的是全局变量的0，因此fail[1]=0，所以经过getfail(0)后返回的结果是1，所以$ch[1]{[}^{\prime }{e}^{\prime }{-}^{\prime }{a}^{\prime }]=ch[1][4]$，由于我们初始化$ch[][]$都为0了，所以此时$ch[1][4]=0$，即$fail[2]=ch[1][4]=0$，也就是说当前新建的这个节点E它的fail指针指向偶根0，这与我们之前所说的单个字符的fail指针指向的是偶根0 是等同的。然后将创建出来的这个节点编号$x=2$赋给now的儿子$ch[now][4]$，表示已经把now的孩子c已经建立出来了。接着让last移动到新创建的这个节点，最后统计一下last状态节点所表示的回文串的出现次数即可。

插入完第一个字符E后，此时now=1，接着插入第二个字符E，s[2]=E，last=2，执行getfail(2)后返回结果为1，即2号点的fail指针是奇根1，所以now=1，发现now已经存在E这个节点了，于是不需要再建立出来了。

通过这两步我们就能理解为什么需要变量$last$了，有了变量$last$，我们就能知道回文树中是否已经存在了我们当前即将插入的这个字符c的节点了。不然的话，我们会重复插入。

---

核心思路

有了上面的前置知识，那么我们来解决这题：

题目想要求的是所有回文子串中的最大存在值，而每个回文串的最大存在值=该回文串出现的次数$\times$ 该回文串的长度

由回文树可知，利用回文树可以统计直接统计出每个回文串出现的次数和回文串的长度，因此这题可以直接使用回文树来解决。

---

代码

#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 3e5+10;
typedef long long LL;
/*
//len[i]:表示编号为i的这个节点所表示的回文串的长度
//ch[i][c]:表示在编号为i的节点所表示的回文串前后两端加上字符c后所形成的新的回文串
//这个新的回文串可以用一个节点来表示 也就是ch[i][c] ch[i][c]也就是新的回文串所对应的状态节点
//fail[i]:表示节点i失配后应该跳转到不等于自身的最长回文后缀所对应的节点
//cnt[i]:表示节点i所表示的回文串的出现次数
//last:表示上一个插入字符所在的节点
//tot:表示这个回文树中添加的节点个数(不包括奇根和偶根) 我们用tot=0来表示了$字符
//因此tot是从1开始来表示题目中输入的字符的
//sz:表示这个回文数中的节点总数(包括奇根和偶根) 初始化时sz=-1,然后规定sz=0表示偶根 sz=1表示奇根
// 最终sz=tot+1
//n添加的字符个数
 */
int sz, tot, last;
int cnt[N], ch[N][26], len[N], fail[N];
char s[N];  //字符串  下标从1开始

int node(int x) //建立一个新节点，长度为x
{
    sz++;   //新建了一个节点  因此节点总数+1
    memset(ch[sz], 0, sizeof(ch[sz]));  //该节点目前还没有孩子节点
    len[sz] = x;    //sz这个节点的所表示的回文长度为x 就是它自身的长度
    //对于新插入的一个字符  我们都规定它的fail指向的是偶根0
    fail[sz] = cnt[sz] = 0;
    return sz;  //得到新建出来的这个节点的编号
}

void init() //初始化
{
    sz = -1;
    last = 0;
    s[tot] = '$';
    node(0);    //建立偶根节点
    node(-1);   //建立奇根节点
    //特殊地规定 0号点的fail指针指向1 也就是偶根的fail指向的是奇根
    //非0、1号点并且后缀中不存在回文串的节点(其实也就是单个字符)不指向它本身，而是指向0
    fail[0] = 1;
}

int getfail(int x) //找后缀回文
{
    //查看区间[tot - len[x],tot-1]内的字符串S已经是回文串了
    //s[tot - len[x] - 1]是S左端点前面的一个字符  s[tot]是S右端点的下一个新增的字符c  如果它俩不匹配
    //那么就顺着fail指针去到这个字符串S的内部寻找最大的回文后缀
    while (s[tot - len[x] - 1] != s[tot])
        x = fail[x];
    return x;   //找到了最大的回文后缀
}

void insert(char c) //建树
{
    s[++tot] = c;
    //设此时得到的回文后缀所对应的节点是now  设其回文后缀是Q
    int now = getfail(last);
    if (!ch[now][c - 'a'])
    {
        //在回文后缀前后两端添加字符c后 得到回文串cQc 对应的状态节点是x 同时其回文长度是len[now] + 2
        int x = node(len[now] + 2);
        //注意下面的这两个顺序不能相反

        //找到x的fail指针应该连向的节点是哪个  那么我们就顺着now的fail指针走 直到不能走为止
        fail[x] = ch[getfail(fail[now])][c - 'a'];
        ch[now][c - 'a'] = x;
    }
    last = ch[now][c - 'a'];    //将当前节点ch[now][c - 'a']给last  更新last
    cnt[last]++;    //last状态节点所表示的回文串的出现次数+1
}

LL query()
{
    LL ans = 0;
    //这里需要从sz遍历到0  因为fail[0]=1是存在的
    //cnt[p]表示回文串p出现的次数 我们知道p表示的是最长回文串 不妨设p="cQcQc",那么每次p出现的时候
    //其回文后缀cQc,c是不是也跟着出现一次呢  因此我们当p出现的时候
    //我们一定要记得把p中的回文后缀的出现次数也更新  即也要更新cQc和c的出现次数
    for (int i = sz; i >= 0; i--)
        cnt[fail[i]] += cnt[i];
    //这里其实从0到sz也是可以的   只不过由于node(0)时初始化len[0]=0了
    //因此len[0]*cnt[0]=0*cnt[0]=0  不影响答案
    for (int i = 1; i <= sz; i++)   //更新答案
        ans = max(ans, 1LL * len[i] * cnt[i]);
    return ans;
}

int main()
{
    init(); //初始化
    scanf("%s", s + 1);
    for (int i = 1; s[i]; i++)
        insert(s[i]);   //将字符插入到回文树中
    printf("%lld\n",query());
    return 0;
}

---