新的开始-

新的开始

---

题目描述

---

核心思路

这个题目有点特殊，我们把每个矿井都看作图中的一个节点，由于在矿井$i$上建立一个发电站，需要费用$v_i$，也就是说节点上是有权值的。然后题目想要问的是连通所有节点所需要的最小花费，这很明显其实就是想要求最小生成树。

题目中的第一个方法表明了每个节点上是可以有权值的；第二个方法表明了节点之间的边是有权值的。如果只有边权，那么就是我们熟悉的模型，直接求解这个图的最小生成树即可。但是特别之处在于节点也是有权值的，因此我们就不能对这张图直接求解最小生成树了。需要做如下转化：

我们可以建立一个虚拟源点（超级发电站），如果某个矿井$i$上有权值$v_i$，那么我们就转化为虚拟源点到这个节点之间的边权为$v_i$，也就是说我们巧妙地把节点的权值转移到了虚拟源点与该节点之间的边的权值，而且是等效的。那么，我们通过这么做之后，就会得到一张$n+1$个节点的新图，而且这个新图只有边是有权值的，顶点不再带有权值，于是就转化为了我们熟悉的模型，那么就可以对这张新图直接求解最小生成树了。

如下图所示：

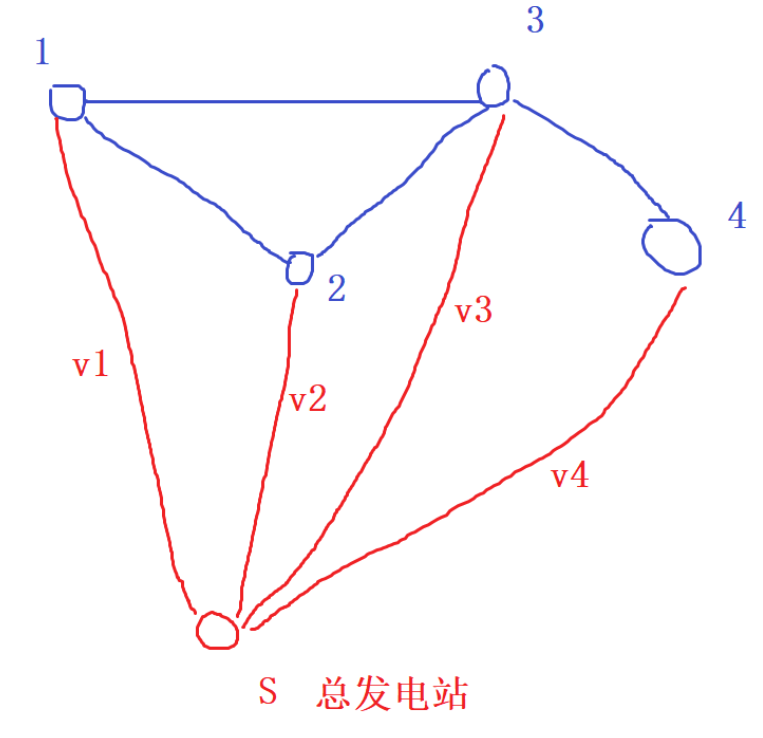
举个栗子：

拿题目样例解释：

---

代码

写法1：prim算法

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=310;
int n;
int g[N][N];
int dist[N];
bool st[N];
//prim算法求解最小生成树
int prim()
{
    int res=0;  //让所有矿井获得充足电能的最小花费
    //初始化每个节点到S集合的距离为正无穷
    memset(dist,0x3f,sizeof dist);
    //初始化虚拟源点到达S集合的距离为0
    dist[0]=0;
    //由于最终形成的最小生成树中有n+1个节点
    //每跑一趟循环就能把一个节点加入S集合,有n+1个节点,因此需要跑n+1次循环
    for(int i=0;i<n+1;i++)
    {
        //t记录的是此时距离S集合最近的点
        int  t=-1;
        for(int j=0;j<=n;j++)
            if(!st[j]&&(t==-1||dist[t]>dist[j]))
                t=j;
        //标记点t已经被加入了S集合
        st[t]=true;
        //累加最小生成树的权值
        res+=dist[t];
        //枚举节点t的所有邻接点  更新这些点到集合S的距离
        for(int k=0;k<=n;k++)
            dist[k]=min(dist[k],g[t][k]);
    }
    return res;
}
int main()
{
    scanf("%d",&n);
    //将矿井节点上的权值vi转化为虚拟源点与该节点之间的边权
    for(int i=1;i<=n;i++)
    {
        int w;
        scanf("%d",&w);
        //最小生成树无向图  
        g[0][i]=g[i][0]=w;
    }
    //输入矿井i和矿井j之间建立电网的费用
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&g[i][j]);
    printf("%d\n",prim());
    return 0;
}

写法2：Kruskal算法

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=310,M=N*N;
int n,cnt;      //cnt是总共的边数
struct Edge{
    int a,b,w;
    bool operator < (const Edge& W)const{
        return w<W.w;
    }
}edges[M];
int p[N];
int find(int x)
{
    if(x!=p[x])
        p[x]=find(p[x]);
    return p[x];
}
int Kruskal()
{
    int res=0;
    sort(edges,edges+cnt);
    for(int i=0;i<=n;i++)
        p[i]=i;
    for(int i=0;i<cnt;i++)
    {
        int a=find(edges[i].a);
        int b=find(edges[i].b);
        int w=edges[i].w;
        if(a!=b)
        {
            p[a]=b;
            res+=w;
        }
    }
    return res;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int w;
        scanf("%d",&w);
        edges[cnt++]={0,i,w};
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            int w;
            scanf("%d",&w);
            edges[cnt++]={i,j,w};
        }
    }
    printf("%d\n",Kruskal());
    return 0;
}

---