拓扑排序----（无所谓，我会出手）

最近刷题一直刷到有向图的拓扑排序，今天也是抽出时间给这玩意搞懂了。

就不在这里粘贴百度搜索的拓扑排序的定义了，莫得意义。

一、首先：
        拓扑排序有三个重要的概念：1.入度、2.出度、3.有向无环图。

1.入度：就是这个点被别的点指向的次数，指向一次入度就是1，指向两次入度就是2

 

 上图中d处的入度就是0，e处的入度为1

2.出度：就是这个点指向别的点的次数，同样的，指向一次就是出度1，指向两次就是出度2

 

 上图中d处的出度就是1，e处的出度为0。

3.有向无环图：从任意一个点出发，经过若干条边之后，没有回到起点处，那么我们就称该图为有向无环图。

 如上图所示，就是一个有向无环图，无论从哪个点出发，都是不能回到原点的。

二、拓扑排序的过程

(1)、从有向图中选择入度为0的顶点并输出；

(2)、在图中删除该顶点和所有以它为起点的有向边；

图示过程如下：

 

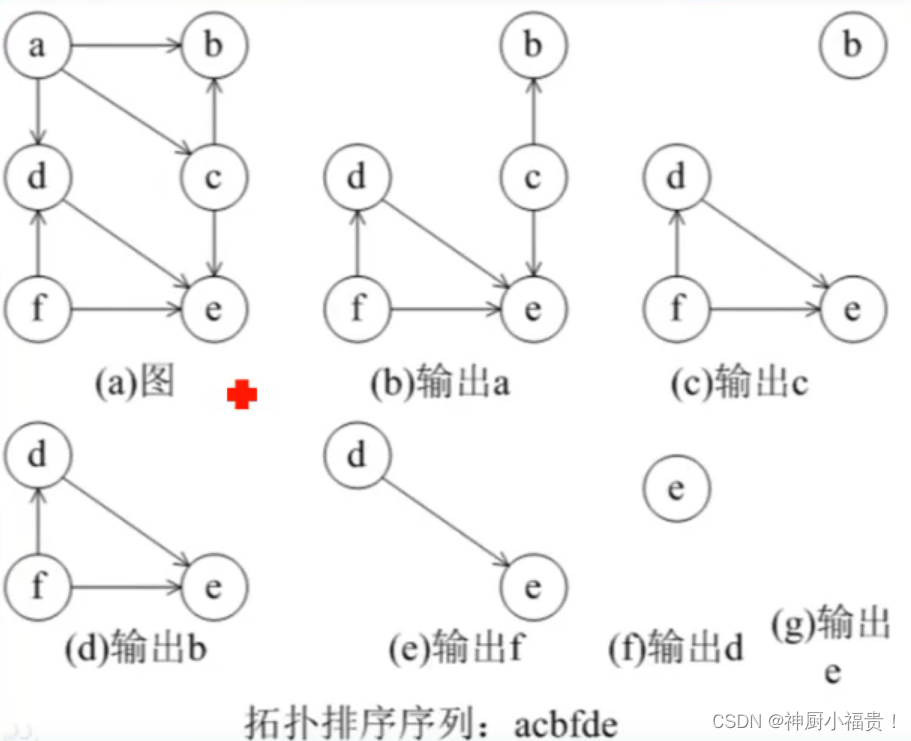
三、看这个题

已知有向图G=（V，E）其中V={V1，V2,V3，V4，V5，V6,V7}、E={<V1,V2>,<V1,V3>,<V1,V4>,<V2,V5>,<V2,V6>,<V3,V5>,<V3,V6>,<V4,V6>,<V5,V7>,<V6,V7>},则它的拓扑排序是啥？

我们首先将题中的有向无环图画出：

 我们发现它的拓扑排序有多种结果：（为了书写方便，只会写出下标，省略掉V）

1 2 3 4 5 6 7

1 3 4 2 6 5 7

等等，只需满足在上述所画的有向无环图中是从右向左的顺序皆可为答案；