BF算法~

先来看BF算法是干嘛的

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。（取自百度百科）

来看图解详细过程：

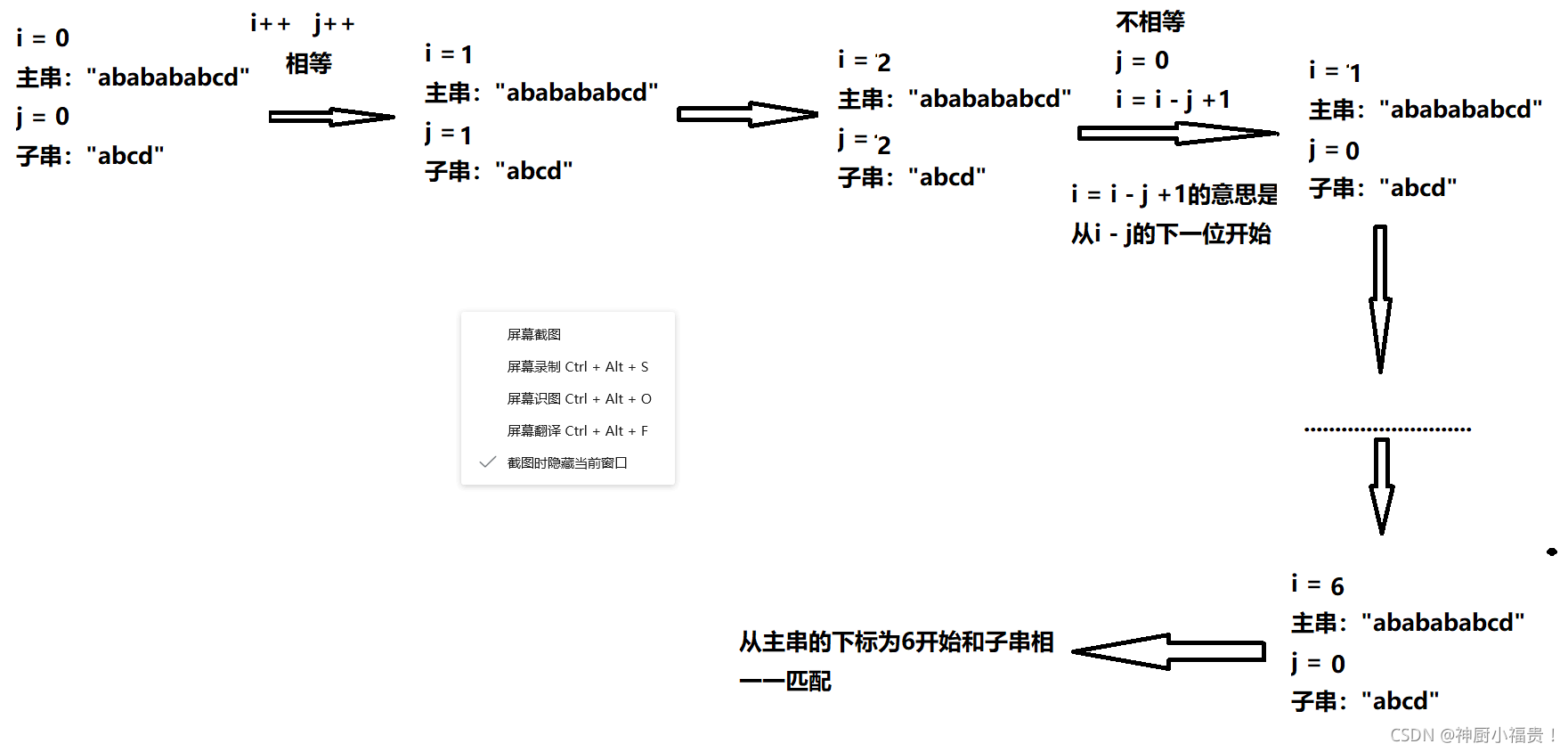
 还有在代码中所说的不能以主串的越界条件来判断是否将子串匹配完：

 

接下来来看代码：

int BF_Search(const char* str, const char* sub, int pos)
{
	assert(str != NULL && sub != NULL);
	if (pos < 0 || pos >= strlen(str))
	{
		return -1;
		//pos = 0; 这种pos越界的情况默认就是从头开始
	}

	int len_str = strlen(str);  //主串的长度
	int len_sub = strlen(sub);   //子串的长度

	int i = pos;//主串开始遍历的位置
	int j = 0; //子串开始的位置
	while (i < len_str && j < len_sub)
	{
		if (sub[j] == str[i])
		{
			i++;
			j++;
		}
		else
		{
			i = i - j + 1;
			j = 0;
		}
	}
	//这会儿循环退出了 要不是i > len_str 或者就是 j > len_sub  又因为主串是否退出不能代表子串与主串是否匹配成功  因此代码为：
	if (j >= len_sub)
	{
		return i - j;
	}
	else   //主串匹配完也没和子串匹配成功  则没有找到  返回-1
	{
		return -1;
	}

}

“要努力，但不要着急，任何硕果累累的结果都是过程的慢慢积累”