图的着色问题，0-1背包问题，单词必须按照字母顺序，所有学生中的已知的朋友圈总数，计算矩阵中所有池塘的大小

一、实验目的及要求

1、世界地图上相邻国家需要用不同的颜色标注以示区别，但最多只需要选取四种颜色即可。请编程实现图的着色问题。

2、编程实现0-1背包问题，至少两种算法。

3、给定一个二维网格和一个单词，找出该单词是否存在于网格中。说明：单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例：board =[ [‘A’,‘B’,‘C’,‘E’], [‘S’,‘F’,‘C’,‘S’], [‘A’,‘D’,‘E’,‘E’]] ，给定 word = “ABCCED”, 返回 true， 给定 word = “SEE”, 返回 true， 给定 word = “ABCB”, 返回 false。

4、班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例1：输入: [[1,1,0], [1,1,0], [0,0,1]] 输出: 2 说明：已知学生0和学生1互为朋友，他们在一个朋友圈。第2个学生自己在一个朋友圈。所以返回2。
示例2：输入: [[1,1,0], [1,1,1], [0,1,1]] 输出: 1 说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

5、你有一个用于表示一片土地的整数矩阵land，该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小，返回值需要从小到大排序。

示例：输入：[[0,2,1,0], [0,1,0,1], [1,1,0,1], [0,1,0,1]] 输出： [1,2,4]

三、实验内容及结果
（包括实验过程、实验数据、实验结果及分析，实验代码另外单独附页）
1、世界地图上相邻国家需要用不同的颜色标注以示区别，但最多只需要选取四种颜色即可。请编程实现图的着色问题。

使用回溯法，有1,2,3,4四种颜色，而地图如关系矩阵所示。从第一个位置颜色为1，接着依次往下遍历，使用与相邻的不同的颜色，如果这样下去无法满足4种颜色填色，则说明之前填色有误，
回溯到之前一个位置，如果该位置4种颜色都不行，则继续回溯直到满足条件。当关系矩阵M如图中所示时，地图的各个位置颜色如输出所示。

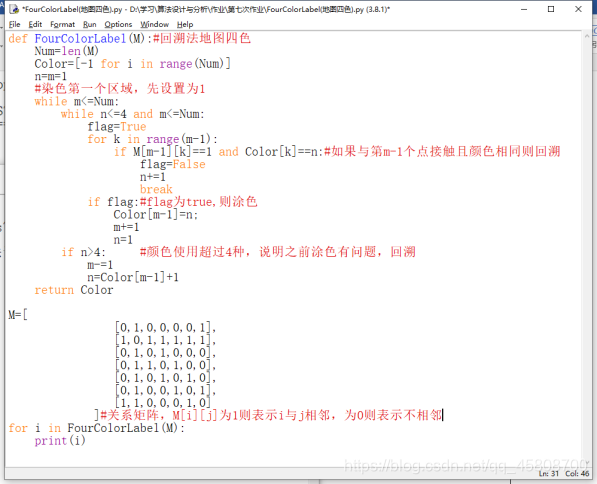
def FourColorLabel(M):#回溯法地图四色
    Num=len(M)
    Color=[-1 for i in range(Num)]
    n=m=1
    #染色第一个区域，先设置为1
    while m<=Num:
        while n<=4 and m<=Num:
            flag=True
            for k in range(m-1):
                if M[m-1][k]==1 and Color[k]==n:#如果与第m-1个点接触且颜色相同则回溯
                    flag=False  
                    n+=1
                    break    
            if flag:#flag为true,则涂色
                Color[m-1]=n;
                m+=1
                n=1
        if n>4:     #颜色使用超过4种，说明之前涂色有问题，回溯
            m-=1
            n=Color[m-1]+1
    return Color
 
M=[
                [0,1,0,0,0,0,1],
                [1,0,1,1,1,1,1],
                [0,1,0,1,0,0,0],
                [0,1,1,0,1,0,0],
                [0,1,0,1,0,1,0],
                [0,1,0,0,1,0,1],
                [1,1,0,0,0,1,0]
             ]#关系矩阵，M[i][j]为1则表示i与j相邻，为0则表示不相邻
for i in FourColorLabel(M):
print(i)

2、编程实现0-1背包问题，至少两种算法。

使用了2种算法，
第一种是动态规划法，使用数组c记录最大价值，c[i][j]表示前i个物体放入容量为j 包的最大价值，c[i-1][j] 表示前i个物体放入容量为j 包的最大价值 ，c[i-1][j-w[i]] 表示前i-1个物体放入容量为j-w[i] 包的最大价值，而c[i][j]到第i个物品时有放入和不放入2种选择，取这2选择的最大值，这样利用动态规划算法可以求出c[i][j]所有的值，能求出最大价值，然后利用show函数输出选择的物品。
第二种方法为回溯法，利用全局变量bestV最大价值currW当前背包重量currV当前背包价值bestx最优选择物品，每次回溯有选并记录当前值与不选往后遍历两种选择，遍历到最后一个物品时与bestV比较。

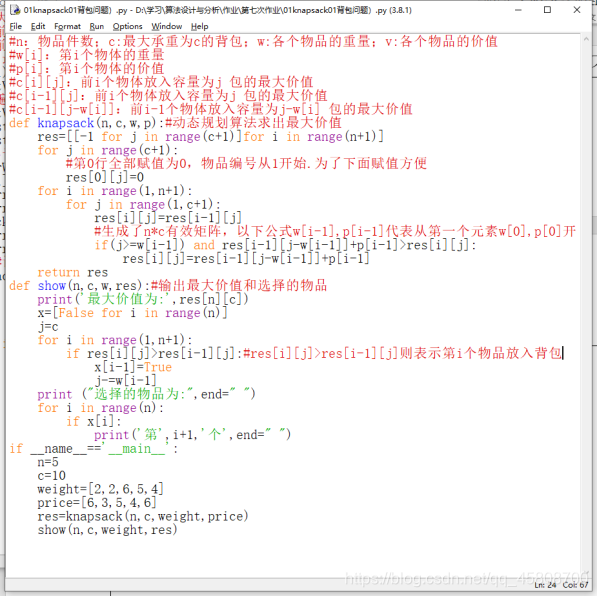
#n：物品件数；c:最大承重为c的背包；w:各个物品的重量；v:各个物品的价值
#w[i]：第i个物体的重量 
#p[i]：第i个物体的价值 
#c[i][j]：前i个物体放入容量为j 包的最大价值 
#c[i-1][j]：前i个物体放入容量为j 包的最大价值 
#c[i-1][j-w[i]]：前i-1个物体放入容量为j-w[i] 包的最大价值
def knapsack(n,c,w,p):#动态规划算法求出最大价值
    res=[[-1 for j in range(c+1)]for i in range(n+1)]
    for j in range(c+1):
        #第0行全部赋值为0，物品编号从1开始.为了下面赋值方便
        res[0][j]=0
    for i in range(1,n+1):
        for j in range(1,c+1):
            res[i][j]=res[i-1][j]
            #生成了n*c有效矩阵，以下公式w[i-1],p[i-1]代表从第一个元素w[0],p[0]开始取。
            if(j>=w[i-1]) and res[i-1][j-w[i-1]]+p[i-1]>res[i][j]:
                res[i][j]=res[i-1][j-w[i-1]]+p[i-1]
    return res
def show(n,c,w,res):#输出最大价值和选择的物品
    print('最大价值为:',res[n][c])  
    x=[False for i in range(n)]  
    j=c  
    for i in range(1,n+1):  
        if res[i][j]>res[i-1][j]:#res[i][j]>res[i-1][j]则表示第i个物品放入背包
            x[i-1]=True  
            j-=w[i-1]  
    print ("选择的物品为:",end=" ")  
    for i in range(n):  
        if x[i]:  
            print('第',i+1,'个',end=" ")
if __name__=='__main__':  
    n=5  
    c=10  
    weight=[2,2,6,5,4]  
    price=[6,3,5,4,6]  
    res=knapsack(n,c,weight,price)  
    show(n,c,weight,res) 

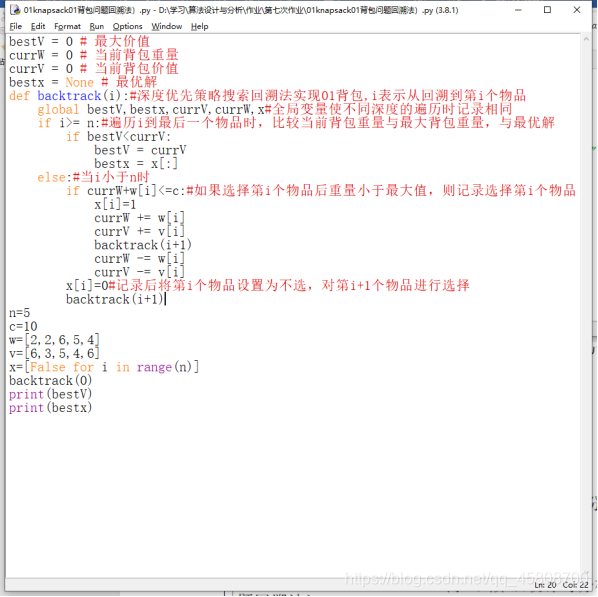
bestV = 0 # 最大价值
currW = 0 # 当前背包重量
currV = 0 # 当前背包价值
bestx = None # 最优解
def backtrack(i):#深度优先策略搜索回溯法实现01背包,i表示从回溯到第i个物品
    global bestV,bestx,currV,currW,x#全局变量使不同深度的遍历时记录相同
    if i>= n:#遍历i到最后一个物品时，比较当前背包重量与最大背包重量，与最优解
        if bestV<currV:
            bestV = currV
            bestx = x[:]
    else:#当i小于n时
        if currW+w[i]<=c:#如果选择第i个物品后重量小于最大值，则记录选择第i个物品后的值
            x[i]=1
            currW += w[i]
            currV += v[i]
            backtrack(i+1)
            currW -= w[i]
            currV -= v[i]
        x[i]=0#记录后将第i个物品设置为不选，对第i+1个物品进行选择
        backtrack(i+1)
n=5
c=10
w=[2,2,6,5,4]
v=[6,3,5,4,6]
x=[False for i in range(n)]
backtrack(0)
print(bestV)
print(bestx)

3、给定一个二维网格和一个单词，找出该单词是否存在于网格中。说明：单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例：board =[ [‘A’,‘B’,‘C’,‘E’], [‘S’,‘F’,‘C’,‘S’], [‘A’,‘D’,‘E’,‘E’]] ，给定 word = “ABCCED”, 返回 true， 给定 word = “SEE”, 返回 true， 给定 word = “ABCB”, 返回 false。
本题利用回溯法解决单词搜索问题，首先directions为四个方向，而从左上角开始，依次改变开始位置，依次往四个方向上在网格中遍历，且用mark记录是否已遍历，如果找不到，则回溯重新遍历，只要有一次开始位置使回溯返回结果为true即返回true。

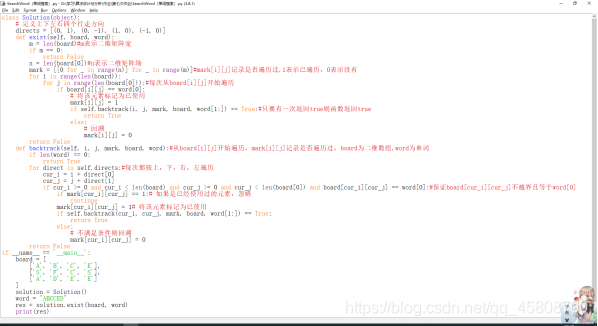
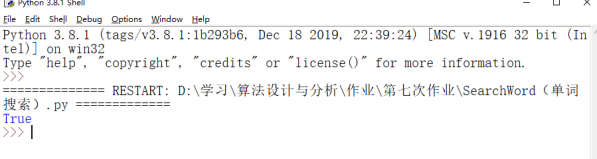
class Solution(object):
    # 定义上下左右四个行走方向
    directs = [(0, 1), (0, -1), (1, 0), (-1, 0)]
    def exist(self, board, word):
        m = len(board)#m表示二维矩阵宽
        if m == 0:
            return False
        n = len(board[0])#n表示二维矩阵场
        mark = [[0 for _ in range(n)] for _ in range(m)]#mark[i][j]记录是否遍历过,1表示已遍历，0表示没有 
        for i in range(len(board)):
            for j in range(len(board[0])):#每次从board[i][j]开始遍历
                if board[i][j] == word[0]:
                    # 将该元素标记为已使用
                    mark[i][j] = 1
                    if self.backtrack(i, j, mark, board, word[1:]) == True:#只要有一次返回true则函数返回true
                        return True
                    else:
                        # 回溯
                        mark[i][j] = 0
        return False
    def backtrack(self, i, j, mark, board, word):#从board[i][j]开始遍历，mark[i][j]记录是否遍历过，board为二维数组,word为单词
        if len(word) == 0:
            return True   
        for direct in self.directs:#每次都按上，下，右，左遍历
            cur_i = i + direct[0]
            cur_j = j + direct[1]
            if cur_i >= 0 and cur_i < len(board) and cur_j >= 0 and cur_j < len(board[0]) and board[cur_i][cur_j] == word[0]:#保证board[cur_i][cur_j]不越界且等于word[0]
                if mark[cur_i][cur_j] == 1:# 如果是已经使用过的元素，忽略
                    continue
                mark[cur_i][cur_j] = 1# 将该元素标记为已使用
                if self.backtrack(cur_i, cur_j, mark, board, word[1:]) == True:
                    return True
                else:
                    # 不满足条件则回溯
                    mark[cur_i][cur_j] = 0
        return False
if __name__ == '__main__':
    board = [
        ['A', 'B', 'C', 'E'],
        ['S', 'F', 'C', 'S'],
        ['A', 'D', 'E', 'E']
    ]
    solution = Solution()
    word = "ABCCED"
    res = solution.exist(board, word)
    print(res)

4、班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
示例1：输入: [[1,1,0], [1,1,0], [0,0,1]] 输出: 2 说明：已知学生0和学生1互为朋友，他们在一个朋友圈。第2个学生自己在一个朋友圈。所以返回2。
示例2：输入: [[1,1,0], [1,1,1], [0,1,1]] 输出: 1 说明：已知学生0和学生1互为朋友，学生1和学生2互为朋友，所以学生0和学生2也是朋友，所以他们三个在一个朋友圈，返回1。

使用宽度优先遍历搜索算法，依次遍历，当该点能够到达其他点即为朋友时，使他们的queue设为同1值，且res+1即朋友圈数+1,且将遍历的点踢出点集。

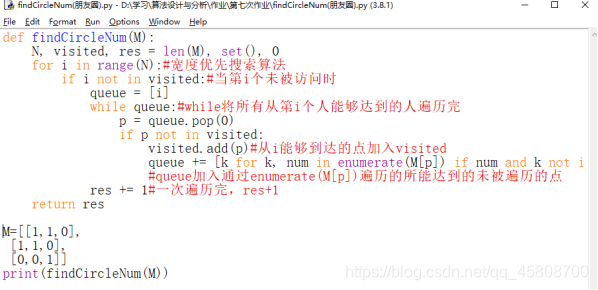
def findCircleNum(M):
    N, visited, res = len(M), set(), 0
    for i in range(N):#宽度优先搜索算法
        if i not in visited:#当第i个未被访问时
            queue = [i]
            while queue:#while将所有从第i个人能够达到的人遍历完
                p = queue.pop(0)
                if p not in visited:
                    visited.add(p)#从i能够到达的点加入visited
                    queue += [k for k, num in enumerate(M[p]) if num and k not in visited]
                    #queue加入通过enumerate(M[p])遍历的所能达到的未被遍历的点
            res += 1#一次遍历完，res+1
    return res

M=[[1,1,0],
 [1,1,0],
 [0,0,1]]
print(findCircleNum(M))

5、你有一个用于表示一片土地的整数矩阵land，该矩阵中每个点的值代表对应地点的海拔高度。若值为0则表示水域。由垂直、水平或对角连接的水域为池塘。池塘的大小是指相连接的水域的个数。编写一个方法来计算矩阵中所有池塘的大小，返回值需要从小到大排序。
示例：输入：[[0,2,1,0], [0,1,0,1], [1,1,0,1], [0,1,0,1]] 输出： [1,2,4]

该题也利用宽度优先遍历算法，当找到一个高度为0时，向垂直、水平或对角连接八个方向依次遍历，且对遍历过的点设置已访问，当8个方向都没有高度为0时，记下这个池塘的大小，然后从其他高度为0的点继续遍历记下大小，最后返回从小到大排序后的结果。

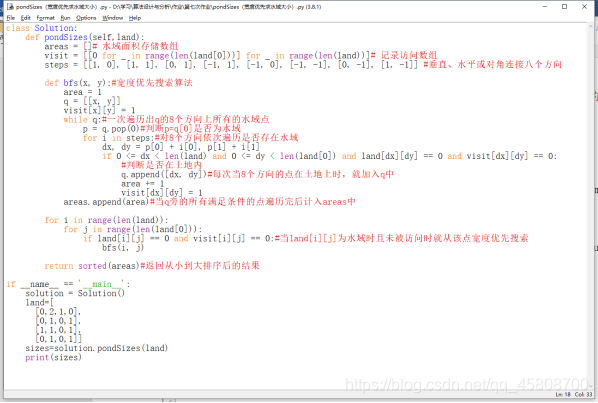
class Solution:
    def pondSizes(self,land):
        areas = []# 水域面积存储数组
        visit = [[0 for _ in range(len(land[0]))] for _ in range(len(land))]# 记录访问数组
        steps = [[1, 0], [1, 1], [0, 1], [-1, 1], [-1, 0], [-1, -1], [0, -1], [1, -1]] #垂直、水平或对角连接八个方向

        def bfs(x, y):#宽度优先搜索算法
            area = 1        
            q = [[x, y]]
            visit[x][y] = 1
            while q:#一次遍历出q的8个方向上所有的水域点
                p = q.pop(0)#判断p=q[0]是否为水域
                for i in steps:#对8个方向依次遍历是否存在水域
                    dx, dy = p[0] + i[0], p[1] + i[1]
                    if 0 <= dx < len(land) and 0 <= dy < len(land[0]) and land[dx][dy] == 0 and visit[dx][dy] == 0:
                        #判断是否在土地内
                        q.append([dx, dy])#每次当8个方向的点在土地上时，就加入q中
                        area += 1
                        visit[dx][dy] = 1
            areas.append(area)#当q旁的所有满足条件的点遍历完后计入areas中

        for i in range(len(land)):
            for j in range(len(land[0])):
                if land[i][j] == 0 and visit[i][j] == 0:#当land[i][j]为水域时且未被访问时就从该点宽度优先搜索
                    bfs(i, j)

        return sorted(areas)#返回从小到大排序后的结果

if __name__ == '__main__':
    solution = Solution()
    land=[
      [0,2,1,0],
      [0,1,0,1],
      [1,1,0,1],
      [0,1,0,1]]
    sizes=solution.pondSizes(land)
    print(sizes)

四、实验总结
（根据实验写出一些心得或分析等）
这次实验让我更加体会了回溯法与深度宽度遍历算法，虽然算法很好理解，但在代码编写时感觉有些困难，对许多细节方面有所不足。