4. 寻找两个正序数组的中位数（笔记）

最新推荐文章于 2025-03-27 16:30:45 发布

如风的少年-

最新推荐文章于 2025-03-27 16:30:45 发布

阅读量171

点赞数

分类专栏： LeetCode 文章标签： leetcode c++ 数据结构 python

原文链接：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/

版权

数组排序中位数二分查找算法

关键词由优快云通过智能技术生成

LeetCode 专栏收录该内容

12 篇文章

订阅专栏

寻找两个正序数组的中位数
 视频题解
请添加图片描述
在这里插入图片描述

左边元素SIZEleft个数是确定的，是(m+n+1) / 2个元素，所以只需要在一个数组中确定分隔线的位置，通过(m+n+1)/2，就可以计算出另外一个数组中分割线的位置

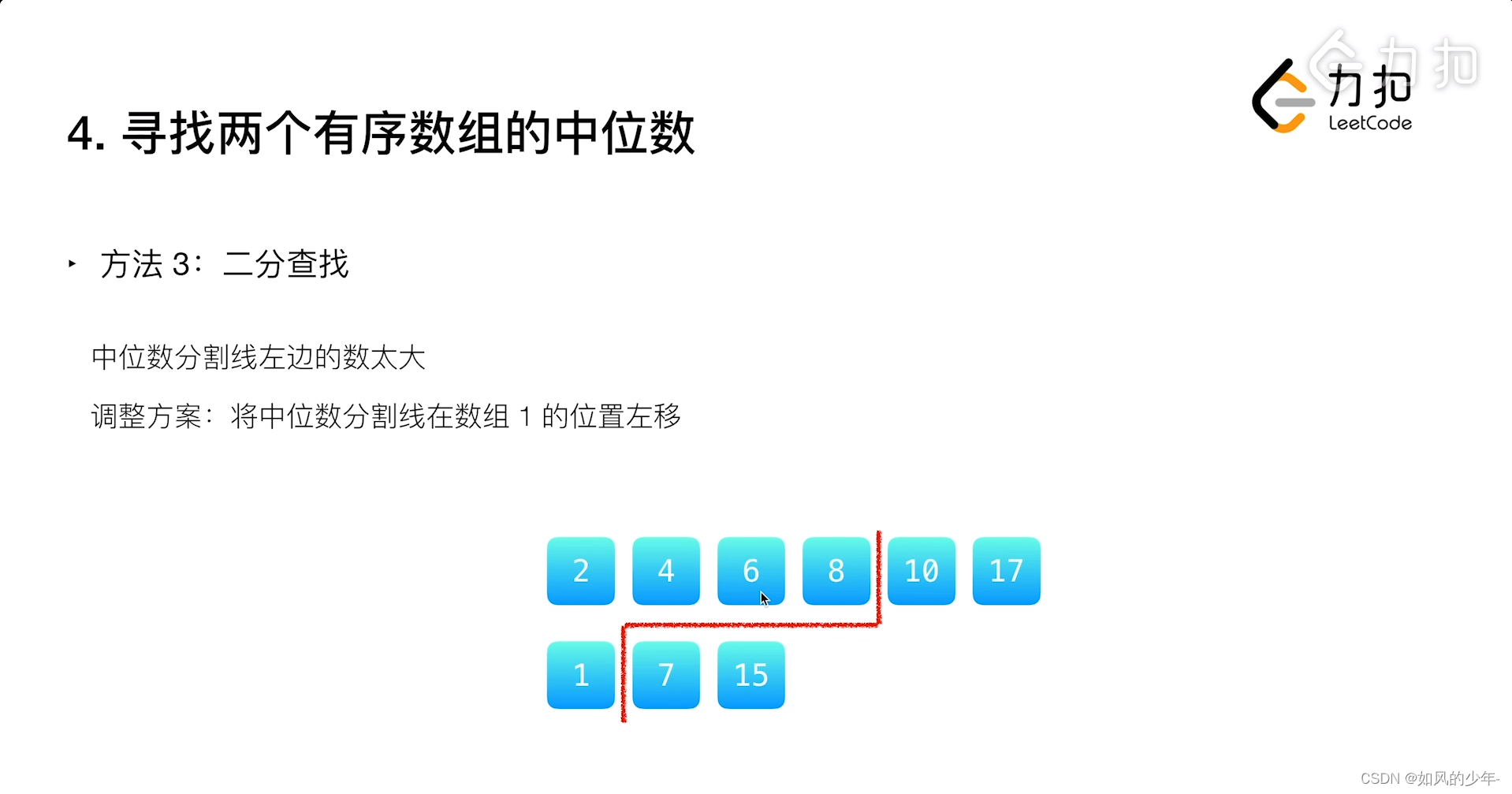
在这里插入图片描述
对于第一个数组而言，分隔线右边的数6<第二个数组中分隔线右边的数8
这是由于第一个分割线右边的数太小导致的，所以让第一个分割线右移

当两个数组的长度不相等时，可能会出现两种极端的情况，第一个数组中的元素全部在分隔线的左边或者全部在分隔线的右边
在这里插入图片描述

为了方便，在这里将i、j当做分隔线右边的第一个元素
在这里插入图片描述

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size())    swap(nums1, nums2);
        int n = nums2.size(), m = nums1.size();

        int totalLeft = (m+n+1) / 2;//分隔线左边元素的个数
        int left = 0, right = m;  //对于nums1而言，采用二分查找来确定分隔线的位置
        //nums1[i-1] <= nums[j] && nums1[i] >= nums[j-1]满足交叉相等的条件，就说明找到了分隔线的位置
        while(left < right){
            int i = left + (right - left) / 2;
            int j = totalLeft - i;
            if (nums1[i] < nums2[j-1]){//说明分隔线左边的数太小，需要将分割线右移[i+1....right]
                left = i+1;
            }else{                      //[left...i]
                right = i;
            }
        }

        int i = left, j = totalLeft - i;
        int nums1LeftMax = i == 0 ? INT_MIN : nums1[i-1];
        int nums2LeftMax = j == 0 ? INT_MIN : nums2[j-1];
        int nums1RightMin = i == m ? INT_MAX : nums1[i];
        int nums2RightMin = j == n ? INT_MAX : nums2[j];
        if (m+n & 1)    return max(nums1LeftMax, nums2LeftMax);
        else    return (double)(max(nums1LeftMax, nums2LeftMax) + min(nums1RightMin, nums2RightMin)) / 2.0;
    }
};

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        if (len(nums1) > len(nums2)):
            temp = nums1
            nums1 = nums2
            nums2 = temp

        m, n = len(nums1), len(nums2)
        totalLeft = int((m + n + 1) / 2)
        left, right = 0, m

        while left < right:
            i = int((left + right) / 2)
            j = int(totalLeft - i)
            if nums1[i] <= nums2[j - 1]:
                left = i + 1
            else:
                right = i

        i = int(left)
        j = int(totalLeft - i)
        MAX, MIN = 0x3f3f3f3f, -0x3f3f3f3f

        if i == 0:
            nums1LeftMax = MIN
        else:
            nums1LeftMax = nums1[i - 1]

        if j == 0:
            nums2LeftMax = MIN
        else:
            nums2LeftMax = nums2[j - 1]

        if i == m:
            nums1RightMin = MAX
        else:
            nums1RightMin = nums1[i]

        if j == n:
            nums2RightMin = MAX
        else:
            nums2RightMin = nums2[j]

        if (m+n)%2 == 1:
            return max(nums1LeftMax, nums2LeftMax);
        else:
            return (max(nums1LeftMax, nums2LeftMax) + min(nums1RightMin, nums2RightMin)) / 2