数据结构-排序算法-优快云博客

常见的数据结构算法

1、插入排序

每次确定一个元素在已经有序的位置。

代码

#include<stdio.h>
using namespaces std;
void insert_sort(int a[],int ,n){
	for(int i=1;i<n;i++){
		int key = a[i];
		int j = i-1;
		while(j >= 0 && a[j] > key){
			a[j+1] = a[j];
			j--;
		}
		a[j+1] = key;
	}
}
int main(){
	
}

每次在前方已有序的部分，插入到对应的地方

事件复杂度O(N^2) ，最好可达(n)。空间复杂度O(1)。稳定（值相同的元素在排序前和排序后相对位置不变）

2、选择排序

选择排序就是每次选取最小（最大）的放在已排列集合的后面

#include<stdio.h>
using namespaces std;
void swap(int& a,int& b){
    int temp = a;
    a = b;
    b = temp;
    return;
}
void select_sort(int a[],int ,n){
	for(int i=1;i<n;i++){
		int minnum = i;
		for(int j = i+1; j< n;j++){
			if(a[minnum] > a[j]){
				minnum = j;
			}
		}
        swap(a[minnum],a[i]);	
	}
}
int main(){
	
}

不稳定

3、冒泡排序

复杂度 O(N^2) 稳定的

冒泡太简单，自己写吧

4、希尔排序

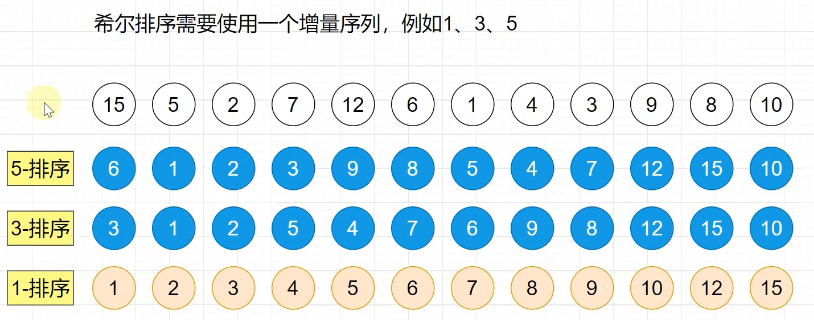
每次都是一个插入排序。只不过间隔不同

希尔排序的复杂度依赖于增量序列。除了一些简单的序列，其他的序列的复杂度证明是一个长期为解决的问题。最坏情况O(n^2 )

希尔排序是不稳定的

5、计数排序

利用数组的下标，进行遍历。给那种哈希差不多

通过计数而不是比较进行排序。

6、快速排序

分而治之，选择一个基准，将比基准大的和小的分开。在将这些部分按照这些思想分割。

#include <bits/stdc++.h>
using namespace std;

void quickSort(vector<int>& nums, int l, int r) {
    if (l >= r) return;
    int temp = nums[l];
    int i = l - 1, j = r + 1;                // Hoare 经典写法
    while (i < j) {
        do i++; while (nums[i] < temp && i<=r);
        do j--; while (nums[j] > temp && j>=l);
        if (i < j) swap(nums[i], nums[j]);
    }
    quickSort(nums, l, j);
    quickSort(nums, j + 1, r);
}

int main() {
    vector<int> nums = {9, 7, 5, 6, 19, 3};
    quickSort(nums, 0, nums.size() - 1);
    for (int x : nums) cout << x << ' ';
    return 0;
}

7、堆排序

大顶堆

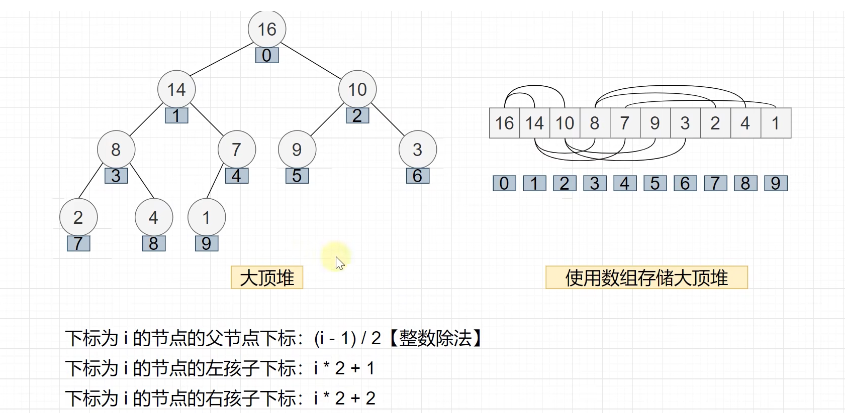
小顶堆

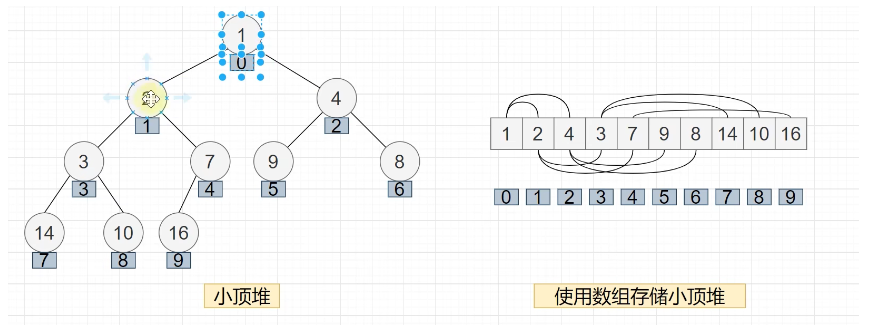
要满足堆的性质，需要父节点与子节点比较，交换位置。

复杂度O(log N)

#include <bits/stdc++.h>
using namespace std;

//维护堆 arr 数组  n 数组长度
void heapify(int arr[],int n,int i){
	int largest = i;
	int lson = i * 2 + 1;
	int rson = i * 2 + 2;
	if(lson < n && arr[largest] < arr[lson])
		largest = lson;
	if(lson < n && arr[largest] < arr[rson])
		largest = rson;
	if(largest != i){
		swap(&arr[laregst],&arr[i]);
		heapify(arr,n,laregst);
	}
}
//堆排序 入口
void heap_sort(int arr[], int n){
	int i;
	//建堆
	for(i = (n - 1) / 2; i >= 0; i--){
		heapify(arr,n,i);
	}
	//排序
    for(int n -1;i > 0;i--){
        swap(&arr[i],&arr[0]);
        heapify(arr,i,0);
    }
}

下沉是堆排序的唯一核心操作；上浮只在“插入新元素”这种动态维护场景里才用得到。