线性代数
1. 基础概念和符号
线性代数提供了一种紧凑地表示和操作线性方程组的方法。例如，以下方程组：
在矩阵表示法中，我们可以更紧凑地表达：
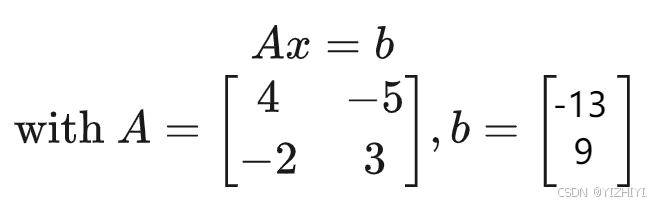
1.1 基本符号
我们使用以下符号：
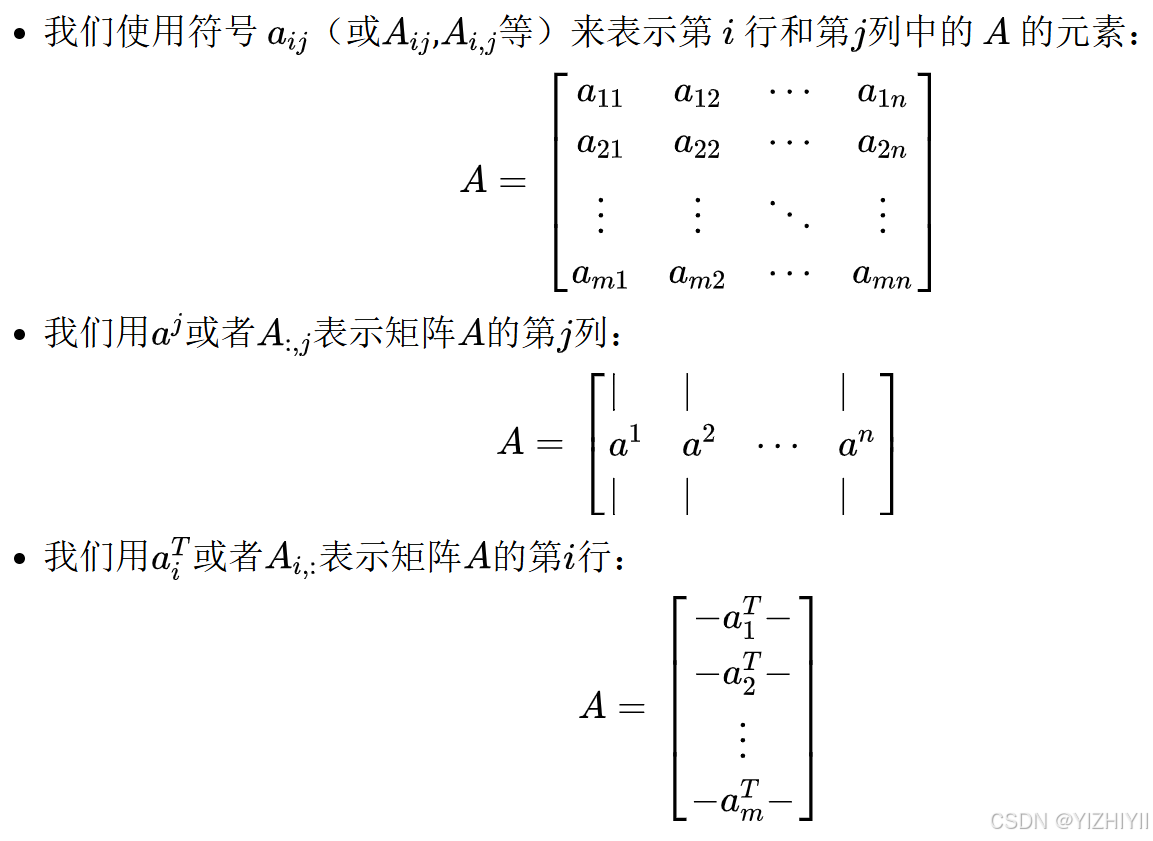
在许多情况下，将矩阵视为列向量或行向量的集合非常重要且方便。 通常，在向量而不是标量上操作在数学上（和概念上）更清晰。只要明确定义了符号，用于矩阵的列或行的表示方式并没有通用约定。
2.矩阵乘法
2.1 向量-向量乘法
2.2 矩阵-向量乘法
2.3 矩阵-矩阵乘法
这些不同方法的直接优势在于它们允许您在向量的级别/单位而不是标量上进行操作。
为了完全理解线性代数而不会迷失在复杂的索引操作中，关键是要用尽可能多的概念进行操作。
实际上所有的线性代数都处理某种矩阵乘法，花一些时间对这里提出的观点进行直观的理解是非常必要的。
除此之外，了解一些更高级别的矩阵乘法的基本属性是很有必要的：
3 运算和属性
在本节中，我们介绍矩阵和向量的几种运算和属性。
3.1 单位矩阵和对角矩阵
3.2 转置
矩阵的转置是指翻转矩阵的行和列。
3.3 对称矩阵
3.4 矩阵的迹
3.5 范数
3.6 线性相关性和秩
3.7 方阵的逆
3.8 正交阵
3.9 矩阵的值域和零空间
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
