3.21
hw机试【栈】
NC52 括号序列
题目:给出一个仅包含字符'(',')','{','}','['和']',的字符串,判断给出的字符串是否是合法的括号序列 括号必须以正确的顺序关闭,"()"和"()[]{}"都是合法的括号序列,但"(]"和"([)]"不合法。
-
定义一个栈
Deque<Character> deque = new LinkedList<>(); -
后入先出,遇到后括号就弹出,要保证弹出来的是对应的,并且最后栈内没有剩余,就是合格的(需要多次比较是否匹配,不好)
-
或者直接这样,遇到左括号,压入右括号,就可以直接比较后面右括号与栈顶元素是否相同
-
使用双端队列作为栈使用,用于存储待匹配的右括号
-
从左向右,遇到左括号,就添加对应的右括号
-
如果栈为空或者栈顶元素与当前字符不匹配,说明括号无法正确匹配,返回false
-
判断如果 右括号,判断右括号和栈顶peek是否相等,如果是对应右括号那就弹出该正确右括号pop
注意,返回结果
return deque.isEmpty();而不是if(deque.isEmpty()){ return true; }注意
}else if(deque.peek() == ch){deque.pop();}else if(deque.isEmpty() || deque.peek() != ch){return false;}这样是不对的
要是考虑这样的情况:当遇到一个闭括号时,你应该首先检查栈是否为空。这是因为,如果栈为空,这意味着没有与之匹配的开括号,所以字符串立即被判定为无效。然后,如果栈不为空,你才检查栈顶元素是否与当前的闭括号匹配。这个顺序确保了逻辑的正确性和效率。
}else if (deque.isEmpty() || deque.peek() != ch){ // 如果栈为空,或者栈顶元素与当前字符不匹配,表示括号不匹配 return false; }else{ // 当前字符与栈顶元素匹配,弹出栈顶元素 deque.pop(); }import java.util.*; class Solution { public boolean isValid(String s) { Deque<Character> deque = new LinkedList<>(); char ch; for(int i = 0; i < s.length(); i++){ ch = s.charAt(i); if(ch == '('){ deque.push(')'); }else if(ch == '['){ deque.push(']'); }else if (ch == '{'){ deque.push('}'); }else if(deque.isEmpty() || deque.peek() != ch){ return false; }else{ deque.pop(); } } return deque.isEmpty(); } } -
Leetcode1614 括号的最大嵌套深度
1614. 括号的最大嵌套深度 - 力扣(LeetCode)
如果字符串满足以下条件之一,则可以称之为 有效括号字符串(valid parentheses string,可以简写为 VPS):
字符串是一个空字符串
"",或者是一个不为"("或")"的单字符。字符串可以写为
AB(A与B字符串连接),其中A和B都是 有效括号字符串 。字符串可以写为
(A),其中A是一个 有效括号字符串 。类似地,可以定义任何有效括号字符串
S的 嵌套深度depth(S):
depth("") = 0
depth(C) = 0,其中C是单个字符的字符串,且该字符不是"("或者")"
depth(A + B) = max(depth(A), depth(B)),其中A和B都是 有效括号字符串
depth("(" + A + ")") = 1 + depth(A),其中A是一个 有效括号字符串例如:
""、"()()"、"()(()())"都是 有效括号字符串(嵌套深度分别为 0、1、2),而")("、"(()"都不是 有效括号字符串 。给你一个 有效括号字符串
s,返回该字符串的s嵌套深度 。
直接计数
class Solution {
public int maxDepth(String s) {
int cur = 0;
int max = 0;
for(int i = 0; i < s.length(); i++){
char c = s.charAt(i);
if(c == '('){
cur++;
}else if(c == ')'){
cur--;
}
max = Math.max(cur, max);
}
return max;
}
}
使用栈,慢
class Solution {
public int maxDepth(String s) {
Deque<Character> deque = new LinkedList<>();
int maxSize = 0;
for(int i = 0; i < s.length(); i++){
char ch = s.charAt(i);
if(ch == '('){
// 遇到开括号,入栈
deque.push(')');
// 更新最大深度
maxSize = Math.max(maxSize, deque.size());
} else if(!deque.isEmpty() && ch == deque.peek()){
// 如果栈不为空,并且栈顶元素与当前闭括号匹配,则出栈
deque.pop();
}
}
return maxSize;
}
}
hw机试【排列组合】
Leetcode 面试题08
有重复字符串的排列组合 面试题 08.08. 有重复字符串的排列组合 - 力扣(LeetCode)
有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
-
作用域问题:
res(存储结果的列表)、path(当前路径或当前排列)、以及set(用于检测重复字符的集合)应该被定义为方法外部的变量或作为方法参数传递,以确保在递归调用中可以访问和修改它们。 -
if (i > 0 && chars[i] == chars[i-1] && !used[i-1]) continue;这里的!used[i-1]是说前一个未使用,只有!false才是ture
示例qqe进行组合输出的流程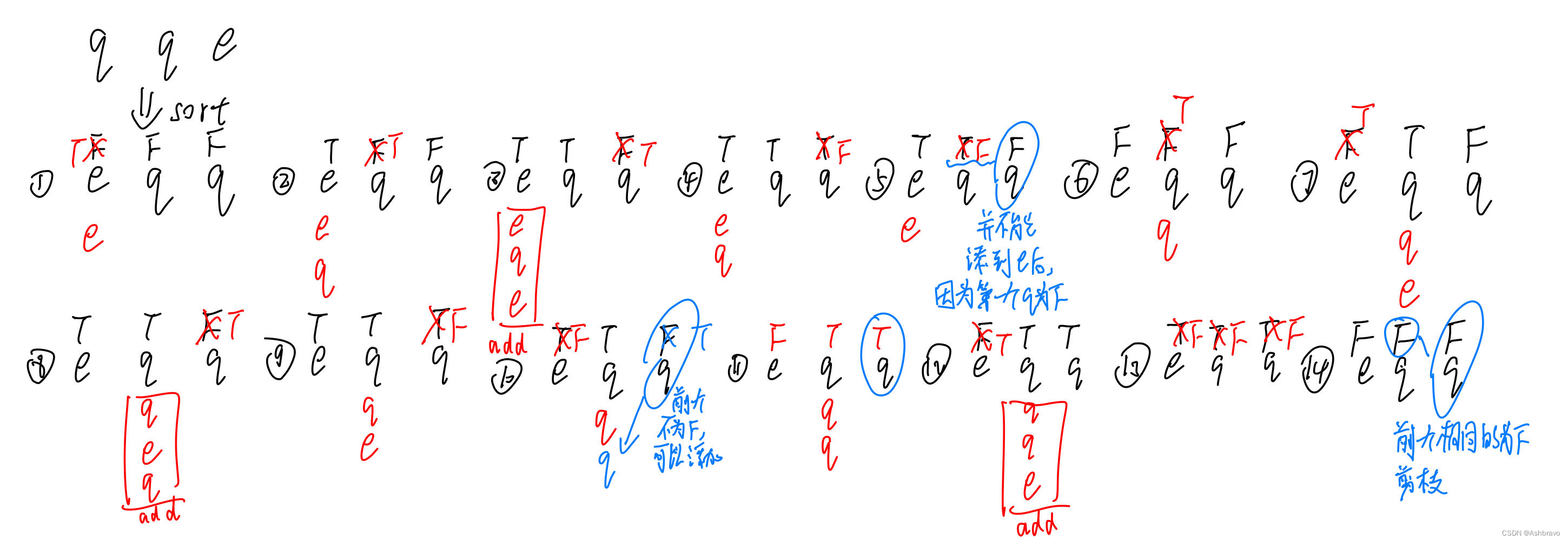
import java.util.ArrayList;
import java.util.List;
public class Solution {
List<String> res = new ArrayList<>();
StringBuilder path = new StringBuilder();
public String[] permutation(String S) {
boolean[] used = new boolean[S.length()];
char[] chars = S.toCharArray();
// 对字符数组进行排序,以方便后面剪枝重复字符
Arrays.sort(chars);
backtrack(chars, used);
return res.toArray(new String[0]);
}
private void backtrack(char[] chars, boolean[] used) {
if (path.length() == chars.length) {
// 当路径长度等于字符数组长度时,将其添加到结果集
res.add(path.toString());
return;
}
for (int i = 0; i < chars.length; i++) {
if (used[i]) continue; // 如果当前字符已经使用过,则跳过
// 剪枝条件,避免重复字符导致的重复结果
if (i > 0 && chars[i] == chars[i-1] && !used[i-1]) continue;
// 做选择
used[i] = true;
path.append(chars[i]);
backtrack(chars, used);
// 撤销选择
used[i] = false;
path.deleteCharAt(path.length() - 1);
}
}
}leetcode 77 组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
二叉树
左叶子之和
左叶子的明确定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
那么判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。
如果该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空,则找到了一个左叶子,判断代码如下:
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
左叶子节点处理逻辑
}
平时我们解二叉树的题目时,已经习惯了通过节点的左右孩子判断本节点的属性,而本题我们要通过节点的父节点判断本节点的属性。
递归法
递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲:
确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int
使用题目中给出的函数就可以了。
确定终止条件
如果遍历到空节点,那么左叶子值一定是0
if (root == NULL) return 0;1
注意,只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0,那么终止条件为:
if (root == NULL) return 0; if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写,如果不写不影响结果,但就会让递归多进行了一层。1 2
确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和。
代码如下:
int leftValue = sumOfLeftLeaves(root->left); // 左 if (root->left && !root->left->left && !root->left->right) { leftValue = root->left->val; } int rightValue = sumOfLeftLeaves(root->right); // 右 int sum = leftValue + rightValue; // 中 return sum;
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if(root == null) return 0;
int leftValue = sumOfLeftLeaves(root.left);
int rightValue = sumOfLeftLeaves(root.right);
int midVaule = 0;
if(root.left != null && root.left.left == null && root.left.right == null){
midVaule = root.left.val;
}
int sum = leftValue + rightValue + midVaule;
return sum;
}
}
迭代
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
// 如果树为空,则左叶子节点的和为0
if (root == null) return 0;
// 使用Stack来支持迭代遍历树
Stack<TreeNode> stack = new Stack<>();
// 将根节点添加到栈中,作为遍历的起点
stack.add(root);
// 初始化结果变量,用于累加所有左叶子节点的值
int result = 0;
// 当栈不为空时,继续遍历
while (!stack.isEmpty()) {
// 从栈中取出一个节点
TreeNode node = stack.pop();
// 检查当前节点的左子节点是否是叶子节点
// 如果是叶子节点(即没有左右子节点),则将其值加到结果中
if (node.left != null && node.left.left == null && node.left.right == null) {
result += node.left.val;
}
// 如果当前节点有右子节点,将右子节点添加到栈中
if (node.right != null) stack.add(node.right);
// 如果当前节点有左子节点,将左子节点添加到栈中
if (node.left != null) stack.add(node.left);
}
// 返回所有左叶子节点值的和
return result;
}
}
计算给定二叉树中所有左叶子节点的值之和的功能,采用了层序遍历的迭代方法。层序遍历,又称为广度优先搜索(BFS),是从根节点开始按层遍历树中的每个节点,从左到右访问同一层的所有节点,然后移动到下一层继续同样的遍历过程。
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
// 初始化左叶子节点值的总和
int sum = 0;
// 如果树为空,则直接返回0
if (root == null) return 0;
// 使用队列来支持层序遍历,队列是先进先出(FIFO)的数据结构
Queue<TreeNode> queue = new LinkedList<>();
// 将根节点加入队列
queue.offer(root);
// 当队列不为空时,循环继续,表示还有节点待处理
while (!queue.isEmpty()) {
// 获取当前层的节点数量
int size = queue.size();
// 遍历当前层的每个节点
while (size-- > 0) {
// 从队列中取出一个节点
TreeNode node = queue.poll();
// 如果当前节点的左子节点不为空
if (node.left != null) {
// 将左子节点加入队列,以便后续遍历其子节点
queue.offer(node.left);
// 如果左子节点是叶子节点(没有左右子节点)
if (node.left.left == null && node.left.right == null) {
// 累加左叶子节点的值到总和中
sum += node.left.val;
}
}
// 如果当前节点的右子节点不为空,也将其加入队列,以便后续遍历
if (node.right != null) queue.offer(node.right);
}
}
// 返回所有左叶子节点值的总和
return sum;
}
}
注意细节
-
递归法:注意左右中加和
int sum = leftValue + rightValue + midVaule; return sum; -
层序迭代:注意从队列中取出每个值(把queue清空)进行判断是否左叶子节点
// 当队列不为空时,循环继续,表示还有节点待处理 while (!queue.isEmpty()) { // 获取当前层的节点数量 int size = queue.size(); // 遍历当前层的每个节点 while (size-- > 0) { // 从队列中取出一个节点 TreeNode node = queue.poll(); // 如果当前节点的左子节点不为空 if (node.left != null) {
找树左下角的值
不能一直向左遍历到最后一个,它未必是最后一行啊。
在树的最后一行找到最左边的值。
如果使用递归法,如何判断是最后一行呢,其实就是深度最大的叶子节点一定是最后一行。
那么如何找最左边的呢?可以使用前序遍历(当然中序,后序都可以,因为本题没有 中间节点的处理逻辑,只要左优先就行),保证优先左边搜索,然后记录深度最大的叶子节点,此时就是树的最后一行最左边的值。
递归三部曲:
确定递归函数的参数和返回值
参数必须有要遍历的树的根节点,还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了,所以递归函数的返回类型为void。
本题还需要类里的两个全局变量,maxLen用来记录最大深度,result记录最大深度最左节点的数值。
代码如下:
int maxDepth = INT_MIN; // 全局变量 记录最大深度 int result; // 全局变量 最大深度最左节点的数值 void traversal(TreeNode* root, int depth)
确定终止条件
当遇到叶子节点的时候,就需要统计一下最大的深度了,所以需要遇到叶子节点来更新最大深度。
代码如下:
if (root->left == NULL && root->right == NULL) { if (depth > maxDepth) { maxDepth = depth; // 更新最大深度 result = root->val; // 最大深度最左面的数值 } return; }
确定单层递归的逻辑
在找最大深度的时候,递归的过程中依然要使用回溯,代码如下:
// 中 if (root->left) { // 左 depth++; // 深度加一 traversal(root->left, depth); depth--; // 回溯,深度减一 } if (root->right) { // 右 depth++; // 深度加一 traversal(root->right, depth); depth--; // 回溯,深度减一 } return;
递归
class Solution {
// 用于记录遍历过程中遇到的最大深度
private int Deep = -1;
// 存储最底层最左边节点的值
private int value = 0;
public int findBottomLeftValue(TreeNode root) {
// 初始化最底层最左边的值为根节点的值
value = root.val;
// 从根节点开始递归查找,初始深度为0
findLeftValue(root, 0);
// 返回找到的最底层最左边的值
return value;
}
private void findLeftValue(TreeNode root, int deep) {
// 如果当前节点为空,则返回,不做任何处理
if (root == null) return;
// 如果当前节点是叶子节点
if (root.left == null && root.right == null) {
// 检查当前叶子节点的深度是否大于之前记录的最大深度
if (deep > Deep) {
// 更新最底层最左边节点的值和最大深度
value = root.val;
Deep = deep;
}
}
// 递归处理左子树,深度加1
if (root.left != null) findLeftValue(root.left, deep + 1);
// 递归处理右子树,深度加1
if (root.right != null) findLeftValue(root.right, deep + 1);
}
}深度优先搜索
class Solution {
// curVal用于存储当前找到的最底层最左边节点的值
int curVal = 0;
// curHeight记录当前遍历到的最大深度
int curHeight = 0;
public int findBottomLeftValue(TreeNode root) {
// 从根节点开始遍历,初始深度为0
dfs(root, 0);
// 遍历结束后,curVal中存储的就是最底层最左边节点的值
return curVal;
}
public void dfs(TreeNode root, int height) {
// 如果当前节点为空,直接返回
if (root == null) {
return;
}
// 每进入一个新的节点,深度加1
height++;
// 先遍历左子树
dfs(root.left, height);
// 再遍历右子树
dfs(root.right, height);
// 检查是否到达了一个更深的层次
// 注意:这个检查是在访问节点之后进行的,因此它实际上给出的是最底层最右边的值,而不是最左边的值
if (height > curHeight) {
curHeight = height;
curVal = root.val;
}
}
}
层序迭代
class Solution{
public int findBottomLeftValue(TreeNode root){
// 初始化变量value来存储最底层最左边的节点的值
int value = 0;
// 使用队列queue来支持层序遍历,队列是先进先出(FIFO)的数据结构
Queue<TreeNode> queue = new LinkedList<>();
// 将根节点加入队列,作为遍历的起点
queue.offer(root);
// 当队列不为空时,继续循环。空队列意味着树已经遍历完毕
while(!queue.isEmpty()){
// 获取当前层的节点数量,这一步是层序遍历的关键
int size = queue.size();
// 遍历当前层的所有节点
for(int i = 0; i < size; i++){
// 从队列中取出队首元素,即当前层的下一个节点
TreeNode node = queue.poll();
// 如果是当前层的第一个节点,则更新value为该节点的值。
// 在每一层的遍历开始时,第一个节点即为该层最左边的节点。
// 由于层序遍历是从上到下进行的,最后更新的value即为最底层最左边的节点的值
if(i == 0){
value = node.val;
}
// 如果当前节点有左子节点,将左子节点加入队列
if(node.left != null){
queue.offer(node.left);
}
// 如果当前节点有右子节点,将右子节点加入队列
if(node.right != null){
queue.offer(node.right);
}
}
}
// 循环结束后,value存储的是最底层最左边节点的值,返回该值
return value;
}
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








