力扣每日一题—盛最多水的容器

题目 

暴力解法 

package com.leetcode;
/**
 * 给定一个长度为 n 的整数数组height，有 n 条垂线，第 i 条线的两个端点是(i, 0)和(i, height[i])
 *
 * 找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水
 *
 * 返回容器可以储存的最大水量
 *
 * 说明：你不能倾斜容器
 */
public class Solution {
    public static void main(String[] args) {
        int[] arr  = {1,8,6,2,5,4,8,3,7};
        int result = maxArea(arr);
        System.out.println(result);
    }

    /**
     * 暴力解法，双for循环，最终会超出时间限制
     * @param height
     * @return
     */
    public static int maxArea(int[] height) {
        int left = 0;                  // 定位到 头
        int right = height.length-1;   // 定位到 尾
        // ans 为结果，min为两个木板的长度最小值
        int ans = 0;
        int min = 0;

        for (;right > 0; right--) {

            // 将尾固定不动，从 0 到 left-1 进行遍历
            // 一次循环完后，right 向前移动 1
            for (left = 0;left < right; left++  ) {
                min = Math.min(height[left], height[right]);        // 返回 x 和 y 中的最小值
                ans = Math.max(ans, (right - left) * min);          // 返回 x 和 y 中的最大值
            }

        }

        return ans;
    }
}

双指针法 

双指针法，其实说到底就是面积由两个变量决定，一个是宽度，一个是最短高度
暴力搜索，只能是逐步移动一个变量，然后是搜索另一个变量，这样无可避免陷入O(n2)
更好的方法就是，掌握一个变量的递增/递减规律，以此作为指针，然后看另一个变量的变化，这样可确保至少一个变量的变化是可控的
就像本例中，宽度从两边逐步往中间缩，宽度是递减的，这是毋庸置疑的，但是怎么收缩，取决于另一个变量影响因变量（面积）的幅度

• 如果移动短边，会导致最小高度是变化的，虽然宽度递减，但是面积的最大值不知道花落谁家，合理竞争选出最大值
• 如果移动长边，会导致宽度减小，最小高度不变或减小，那也就意味着面积总是递减的，搜索范围内的元素失去了竞争的意义，就会增加无意义的搜索行为

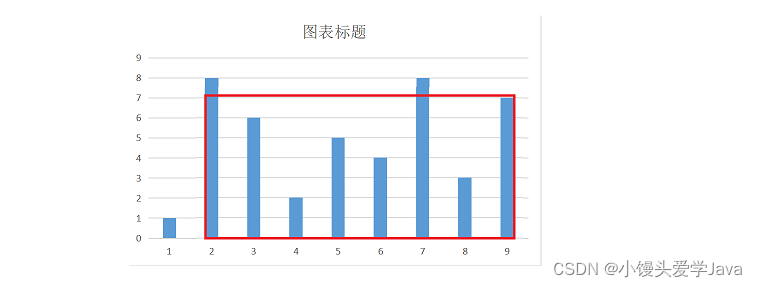
双指针法示意图 

分析：利用双指针移动为什么能够减少遍历次数，我们看下面这张图，如果将短边固定而去移动长边，得到的面积只能是不变或减少，这样只会增加无意义的搜索次数

package com.leetcode;
/**
 * 给定一个长度为 n 的整数数组height，有 n 条垂线，第 i 条线的两个端点是(i, 0)和(i, height[i])
 *
 * 找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水
 *
 * 返回容器可以储存的最大水量
 *
 * 说明：你不能倾斜容器
 */
public class Solution {
    public static void main(String[] args) {
        int[] arr  = {1,8,6,2,5,4,8,3,7};
        int result = maxArea(arr);
        System.out.println(result);
    }

    /**
     * 双指针法
     * @param height
     * @return
     */
    public static int maxArea(int[] height) {
        int left = 0;                  // 定位到 头
        int right = height.length-1;   // 定位到 尾
        // ans 为结果，min为两个木板的长度最小值
        int ans = 0;
        int min = 0;

        while (left < right) {
            min = Math.min(height[left], height[right]);        // 返回 x 和 y 中的最小值
            ans = Math.max(ans, (right - left) * min);          // 返回 x 和 y 中的最大值
            if (height[left] < height[right]) {
                left++;                  // 左边指针加1
            }else {
                right--;                 // left >= right，右边指针减1
            }
        }

        return ans;
    }
}

提交结果：

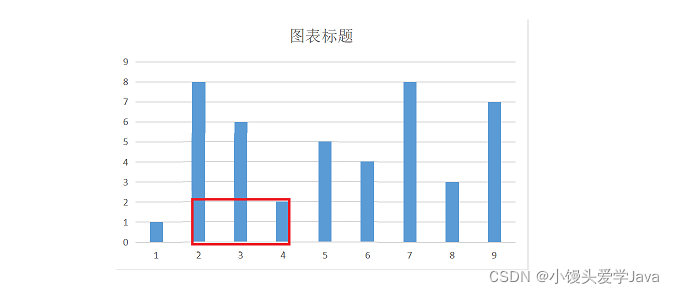
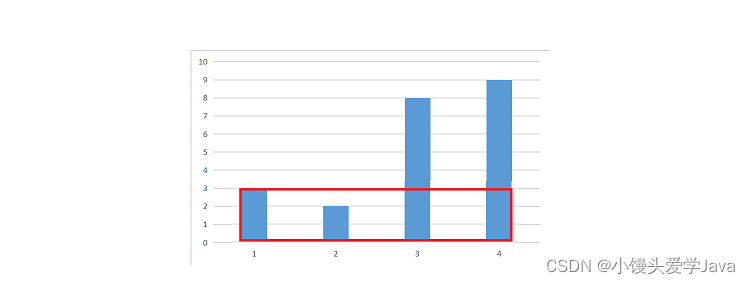
解完后，我们再来回顾一下，有人说，如果第一次移动短边，就导致面积减小，那这次移动也就没有意义，是不是这种情况下双指针法不适用呢？（比如下图这种情况）

答案是否定的，在由两边向中间逐渐靠拢的过程中，面积当然不一定是增大的，如果一直增大那就失去了搜索的意义，或许我们可以这样理解，在中间位置存在很高很高的两条柱形，它们之间的距离为1，但是组成的面积是最大的。不能因为在你迈出第一步发现面积变小之后，就停止了搜索，那必然不能得到令人满意的结果！

最后，力扣每日一题，加油！