二叉树的建立及四种遍历方法

于 2020-01-19 00:04:31 发布
阅读量627 收藏 3
点赞数 2
文章标签： 二叉树 队列 指针 链表 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_45761191/article/details/104030066
版权

二叉树的四种遍历方式：

  • 二叉树的遍历（traversing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问依次且仅被访问一次。
  • 四种遍历方式分别为：先序遍历、中序遍历、后序遍历、层序遍历。

首先声明链表的结点结构定义：

typedef struct tree
{
	int data;
	struct tree* leftchild;
	struct tree* rightchild;
}tree;

一.建立二叉树

先输入根，再输入左子树，最后输入右子树（左边优先）

void build_tree(tree* &L)
{
	int ch;
	cin>>ch;
	if(ch==-1)//-1代表空
	{
		L=NULL;
		return ;
	}
	head=new tree;
	head.data=ch;
	build_tree(head.lefthead);
	build_tree(head.righthead);
	return ;
}

注意：最底层一定要全为-1，表示此处结点为空
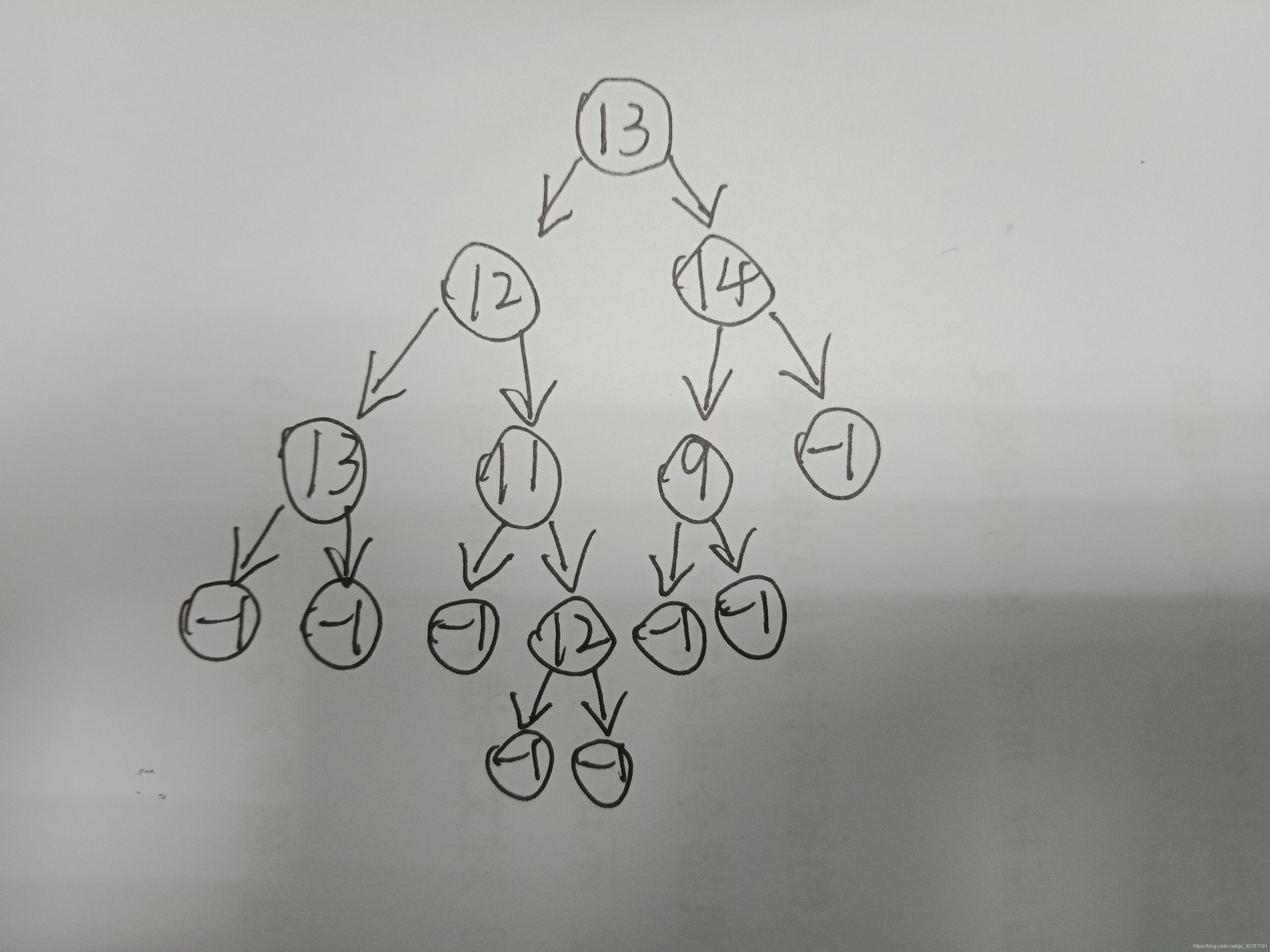
在这里插入图片描述

二.树的遍历

  • 先序遍历：若树为空返回，不为空先访问根节点，再访问左子树，再访问右子树（根左右）

递归法的先序遍历：

void PreOrderTraverse(tree* L)
{
	if(!L)//当L=NULL时返回
	return;
	cout<<L->data<<" ";
	PreOrderTraveral(L->leftchild);
	PreOrderTraveral(L->rightchild);
}

非递归法的先序遍历：首先把根节点压入栈中，此时根节点作为栈顶元素弹出访问。将当前节点的右子树和左子树分别入栈，考虑栈是先入后出因此必须先右子树先入栈，左子树后入栈。重复上述步骤直到栈为空。

typedef struct stack //栈的结构类型
{
	struct stack* next;//指向下一个结点
	tree* k;//指向入栈的树的结点
}stack;
stack* destroy_Stack(stack* head)//释放栈顶元素 
{
	stack* p=head;
	if(p->next==NULL)
	{
		delete p;
		p==NULL;
		return p;
	}
	stack* s=p->next;
	while(s->next)
	{
		p=p->next;
		s=s->next;
	}
	delete s;
	p->next=NULL;
	return p;
}
void PreOrderTravralwithStack(tree* L)//先序遍历非递归 
{
	if(!L)
	return ;
	tree* p=L;
	stack* head=new stack;
	head->next=NULL;
	head->k=L;
	stack* q=head;
	cout<<L->data<<" ";
	while(L->leftchild||L->rightchild)
	{
		if(p->leftchild)
		{
			p=p->leftchild;
			cout<<p->data<<" ";
			stack* s=new stack;
			s->next=NULL;
			s->k=p;
			q->next=s;
			q=s; 
		}
		else if(p->rightchild)
		{
			p=p->rightchild;
			cout<<p->data<<" ";
			stack* s=new stack;
			s->next=NULL;
			s->k=p;
			q->next=s;
			q=s; 
		}
		else
		{
			delete p;
			q=destroy_Stack(head);//通过destroy_Stack返回当前栈顶的地址
			p=q->k;
			if(p->leftchild)//如果p的左节点不是指向空的，那么使它指向空
			p->leftchild=NULL;
			else//如果p的左节点指向空，那么使p的右节点指向空
			p->rightchild=NULL; 
		}
	}
}
  • 中序遍历：若树为空返回，不为空先访问左子树，再访问根节点，再访问右子树（左根右）

递归法的中序遍历：

void InOrderTravral(tree* L)
{
	if(!L)//当L=NULL时返回
	return ;
	InOrderTravral(L->leftchild);
	cout<<L->data<<" ";
	InOrderTravral(L->rightchild);
}

非递归法的中序遍历：中序遍历的非递归版本比前序稍微复杂一点，除了用到辅助栈之外，还需要一个指针 p 指向下一个待访问的节点。如果p的左右孩子指针皆为空，则弹出栈顶元素p，并进行访问，通过destroy_Stack函数，返回当前栈顶元素并使p指向它

void InOrderTravralwithStack(tree* &L)//中序遍历非递归
{
	if(!L)
	return ;
	tree* p=L;
	stack* head=new stack;
	head->next=NULL;
	head->k=L;
	stack* q=head;
	while(1)
	{
		if(p->leftchild)
		{
			stack* s=new stack;
			s->k=p->leftchild;
			s->next=NULL;
			q->next=s;
			q=s;
			p=p->leftchild;
		}
		else if(p->rightchild)
		{
			cout<<p->data<<" ";
			if(p!=head->k)
			{
				q=destroy_Stack(head);
				stack* s=new stack;
				s->k=p->rightchild;
				s->next=NULL;
				q->next=s;
				q=s;
				delete p;
				p=s->k;
			}
			else
			{
				delete head;
				stack* s=new stack;
				s->k=p->rightchild;
				s->next=NULL;
				head=s;
				q=head;
				q->next=NULL;
				delete p;
				p=s->k;
			}
			
		}
		else
		{
			cout<<p->data<<" ";
			if(p==head->k)
			{
				delete p;
				head=NULL;
				p=NULL;
				delete L;
				L=NULL;
				break;
			}
			delete p;
			q=destroy_Stack(head);
			p=q->k;
			if(p->leftchild)
			p->leftchild=NULL;
		}
	}
}
  • 后序遍历：若树为空返回，不为空先访问左子树，再访问右子树，再访问根节点（左右根）

递归法的后序遍历：

void PostOrderTravral(tree* L)
{
	if(!L)//当L=NULL时返回
	return ;
	PostOrderTravral(L->leftchild);
	PostOrderTravral(L->rightchild);
	cout<<L->data<<" ";
}

非递归法的后序遍历：采用一个辅助栈和一个指针p，如果p的左右子树皆为空，则弹出p访问，同时通过destroy_Stack函数返回此时的栈顶元素，如果p是当前栈顶元素的左子树，则当前栈顶元素的左孩子指针指向NULL，如果p是当前栈顶元素的右子树，则当前栈顶元素的右孩子指针指向NULL

void PostOrderTravaralwithStack(tree* &L)
{
	if(!L)
	return ;
	tree* p=L;
	stack* head=new stack;
	head->next=NULL;
	head->k=L;
	stack* q=head;
	while(1)
	{
		if(p->leftchild)
		{
			p=p->leftchild;
			stack* s=new stack;
			s->k=p;
			s->next=NULL;
			q->next=s;
			q=s;
		}
		else if(p->rightchild)
		{
			p=p->rightchild;
			stack* s=new stack;
			s->k=p;
			s->next=NULL;
			q->next=s;
			q=s;
		}
		else
		{
			cout<<p->data<<" ";
			delete p;
			if(head->next==NULL)
            {
                p=NULL;
                L=NULL;
                break;
            }
			q=destroy_Stack(head);
			p=q->k;
			if(p->leftchild)
			p->leftchild=NULL;
			else
			p->rightchild=NULL;
		}
	}
}
  • 层序遍历：若树为空，则空操作返回，否则从树的第一层开始从上到下，从左到右，依次按顺序循环遍历

1.先声明LNode队列结构体

typedef struct
{
	tree* a[1000];//指向入队的结点
	int rear,front;//front为队头，rear为队尾
}LNode;

2.开始层次遍历：

void levelOrder(tree* L)
{
	if(!L)//如果是一个空树则返回
	return ;
	LNode head;
	head.front=0;
	head.a[0]=L;
	head.rear=1;
	while(head.front!=head.rear)//当队头等于队尾时结束循环
	{
		if(head.a[head.front]->leftchild)
		{
			head.a[head.rear]=head.a[head.front]->leftchild;
			head.rear++;
		}
		if(head.a[head.front]->rightchild)
		{
			head.a[head.rear]=head.a[head.front]->rightchild;
			head.rear++;
		}
		cout<<head.a[head.front]->data<<" ";
		head.front++;
	}
}

全部代码：

#include<iostream>
using namespace std;
typedef struct tree//树的结点类型
{
	int data;
	struct tree* leftchild;
	struct tree* rightchild;
}tree;
void build_tree(tree* &L)//建立树
{
	int ch;
	cin>>ch;
	if(ch==-1)
	{
		L=NULL;
		return ;
	}
	L=new tree;
	L->data=ch;
	build_tree(L->leftchild);
	build_tree(L->rightchild);
	return ;
}
void destroy_tree(tree* L)//释放树的空间
{
    if(L==NULL)
        return ;
	if(L->leftchild!=NULL)
	destroy_tree(L->leftchild);
	if(L->rightchild!=NULL)
	destroy_tree(L->rightchild);
	delete L;
	return ;
}
void PreOrderTravral(tree* L)//先序遍历递归
{
	if(!L)
	return;
	cout<<L->data<<" ";
	PreOrderTravral(L->leftchild);
	PreOrderTravral(L->rightchild);
}
typedef struct stack
{
	struct stack* next;
	tree* k;
}stack;
stack* destroy_Stack(stack* head)//释放栈顶元素
{
	stack* p=head;
	if(p->next==NULL)
	{
		delete p;
		p==NULL;
		return p;
	}
	stack* s=p->next;
	while(s->next)
	{
		p=p->next;
		s=s->next;
	}
	delete s;
	p->next=NULL;
	return p;
}
void PreOrderTravralwithStack(tree* L)//先序遍历非递归
{
	if(!L)
	return ;
	tree* p=L;
	stack* head=new stack;
	head->next=NULL;
	head->k=L;
	stack* q=head;
	cout<<L->data<<" ";
	while(L->leftchild||L->rightchild)
	{
		if(p->leftchild)
		{
			p=p->leftchild;
			cout<<p->data<<" ";
			stack* s=new stack;
			s->next=NULL;
			s->k=p;
			q->next=s;
			q=s;
		}
		else if(p->rightchild)
		{
			p=p->rightchild;
			cout<<p->data<<" ";
			stack* s=new stack;
			s->next=NULL;
			s->k=p;
			q->next=s;
			q=s;
		}
		else
		{
			delete p;
			q=destroy_Stack(head);
			p=q->k;
			if(p->leftchild)
			p->leftchild=NULL;
			else
			p->rightchild=NULL;
		}
	}
}
void InOrderTravral(tree* L)//中序遍历递归
{
	if(!L)
	return;
	InOrderTravral(L->leftchild);
	cout<<L->data<<" ";
	InOrderTravral(L->rightchild);
}
void InOrderTravralwithStack(tree* &L)//中序遍历非递归
{
	if(!L)
	return ;
	tree* p=L;
	stack* head=new stack;
	head->next=NULL;
	head->k=L;
	stack* q=head;
	while(1)
	{
		if(p->leftchild)
		{
			stack* s=new stack;
			s->k=p->leftchild;
			s->next=NULL;
			q->next=s;
			q=s;
			p=p->leftchild;
		}
		else if(p->rightchild)
		{
			cout<<p->data<<" ";
			if(p!=head->k)
			{
				q=destroy_Stack(head);
				stack* s=new stack;
				s->k=p->rightchild;
				s->next=NULL;
				q->next=s;
				q=s;
				delete p;
				p=s->k;
			}
			else
			{
				delete head;
				stack* s=new stack;
				s->k=p->rightchild;
				s->next=NULL;
				head=s;
				q=head;
				q->next=NULL;
				delete p;
				p=s->k;
			}
			
		}
		else
		{
			cout<<p->data<<" ";
			if(p==head->k)
			{
				delete p;
				head=NULL;
				p=NULL;
				delete L;
				L=NULL;
				break;
			}
			delete p;
			q=destroy_Stack(head);
			p=q->k;
			if(p->leftchild)
			p->leftchild=NULL;
		}
	}
}
void PostOrderTravral(tree* L)//后序遍历递归
{
	if(!L)
	return;
	PostOrderTravral(L->leftchild);
	PostOrderTravral(L->rightchild);
	cout<<L->data<<" ";
}
void PostOrderTravaralwithStack(tree* &L)
{
	if(!L)
	return ;
	tree* p=L;
	stack* head=new stack;
	head->next=NULL;
	head->k=L;
	stack* q=head;
	while(1)
	{
		if(p->leftchild)
		{
			p=p->leftchild;
			stack* s=new stack;
			s->k=p;
			s->next=NULL;
			q->next=s;
			q=s;
		}
		else if(p->rightchild)
		{
			p=p->rightchild;
			stack* s=new stack;
			s->k=p;
			s->next=NULL;
			q->next=s;
			q=s;
		}
		else
		{
			cout<<p->data<<" ";
			delete p;
			if(head->next==NULL)
            {
                p=NULL;
                L=NULL;
                break;
            }
			q=destroy_Stack(head);
			p=q->k;
			if(p->leftchild)
			p->leftchild=NULL;
			else
			p->rightchild=NULL;
		}
	}
}
typedef struct//队列的结构类型
{
	tree* a[1000];
	int rear,front;
}LNode;
void levelOrder(tree* L)//层次遍历
{
	if(!L)
	return ;
	LNode head;
	head.front=0;
	head.a[0]=L;
	head.rear=1;
	while(head.front!=head.rear)
	{
		if(head.a[head.front]->leftchild)
		{
			head.a[head.rear]=head.a[head.front]->leftchild;
			head.rear++;
		}
		if(head.a[head.front]->rightchild)
		{
			head.a[head.rear]=head.a[head.front]->rightchild;
			head.rear++;
		}
		cout<<head.a[head.front]->data<<" ";
		head.front++;
	}
}
int main()
{
	tree* L;
	build_tree(L);
	InOrderTravralwithStack(L);
	destroy_tree(L);
	return 0;
}

总结:先序遍历、中序遍历、后序遍历的非递归思想都是依靠栈实现的；层次遍历是依靠队列实现的

JaronJiang
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值