浅学一维傅里叶变换【下一章发布 ： 快速二维傅里叶变换FFT、快速二维傅里叶逆变换IFFT】

程序代码如下：

clear
%对数列：1，2，4，4进行傅里叶变换
y1 = [1 2 4 4];
[fy1,sumY1] = Fourier2(y1);
%对函数：y = sin（x）进行傅里叶变换
y2 = @(x) sin(x);
[fy2,sumY2] = Fourier2(y2,1,0,10);
%对数列：1，2，4，5，6，7，8，9进行傅里叶变换
y3 = [1 2 3 4 5 6 7 8 9 ];
[fy3,sumY3] = Fourier2(y3);
%对函数：y = sin（x）-cos（x）进行傅里叶变换
y4 = @(x) sin(x)-cos(x);
[fy4,sumY4] = Fourier2(y4,1,0,10);

程序运行图如下：

1、对变量的截图

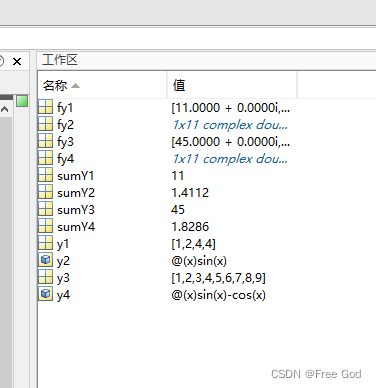
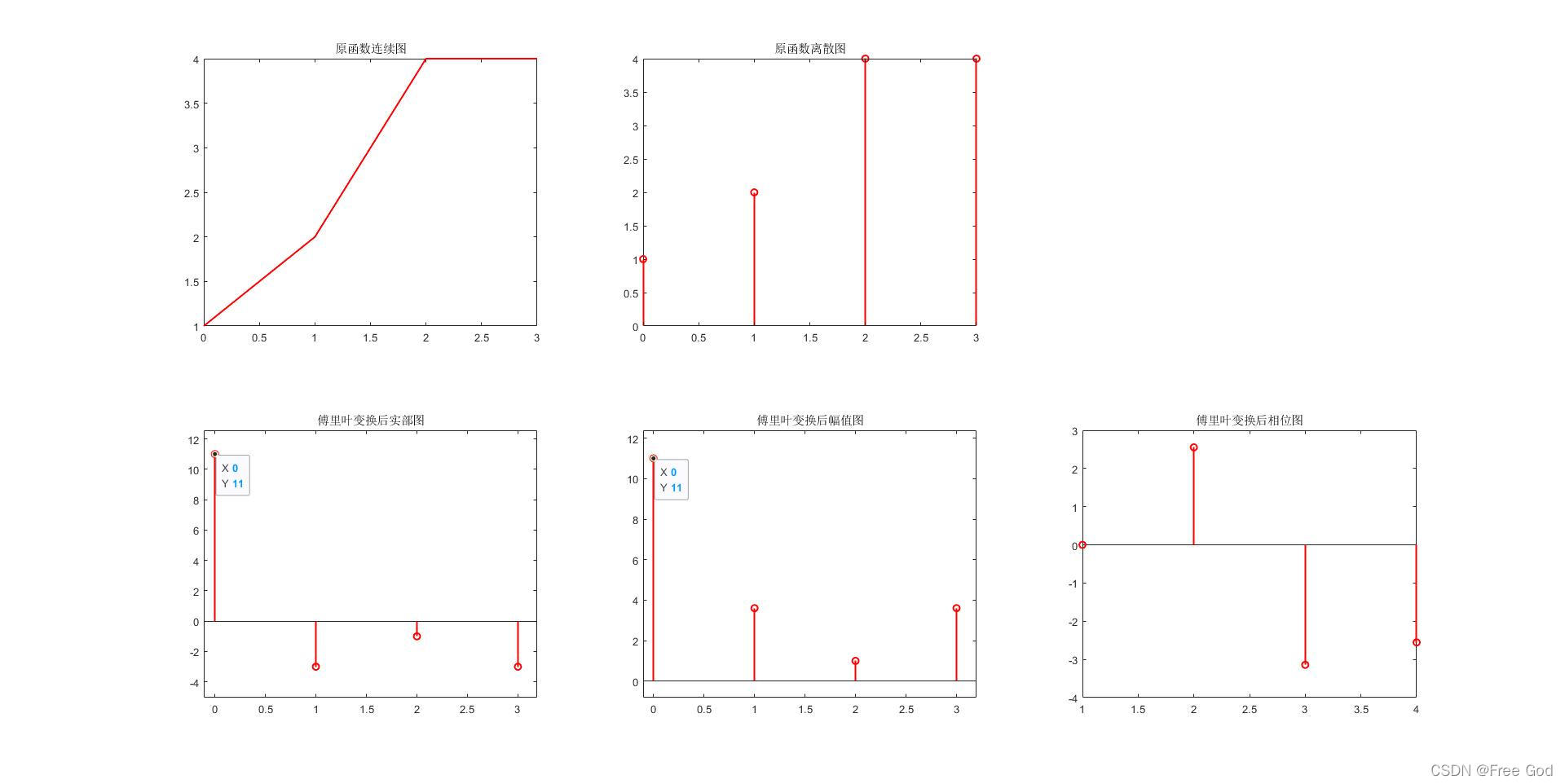
1、对 y = [1 2 4 4]进行离散傅里叶变换

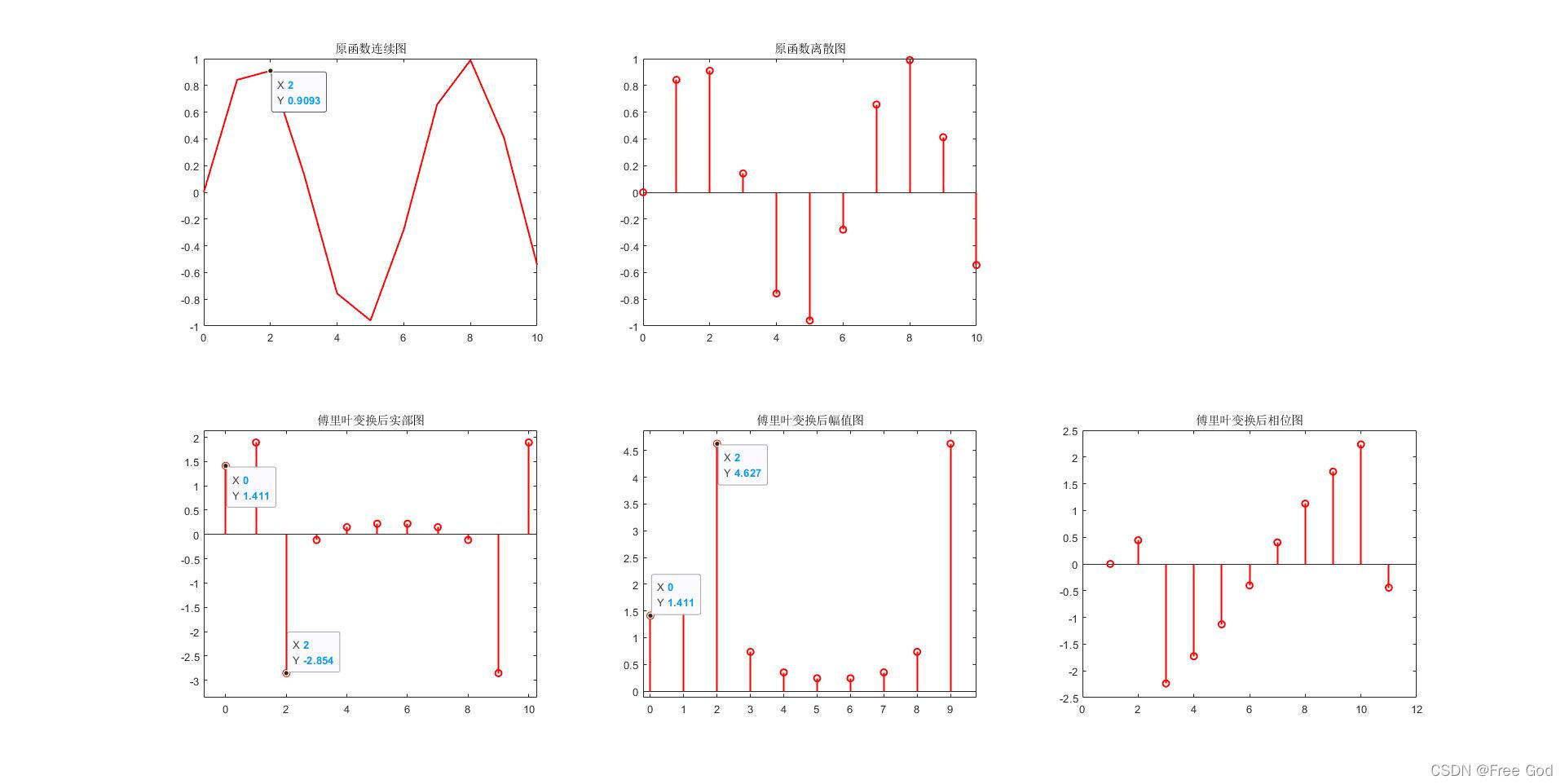
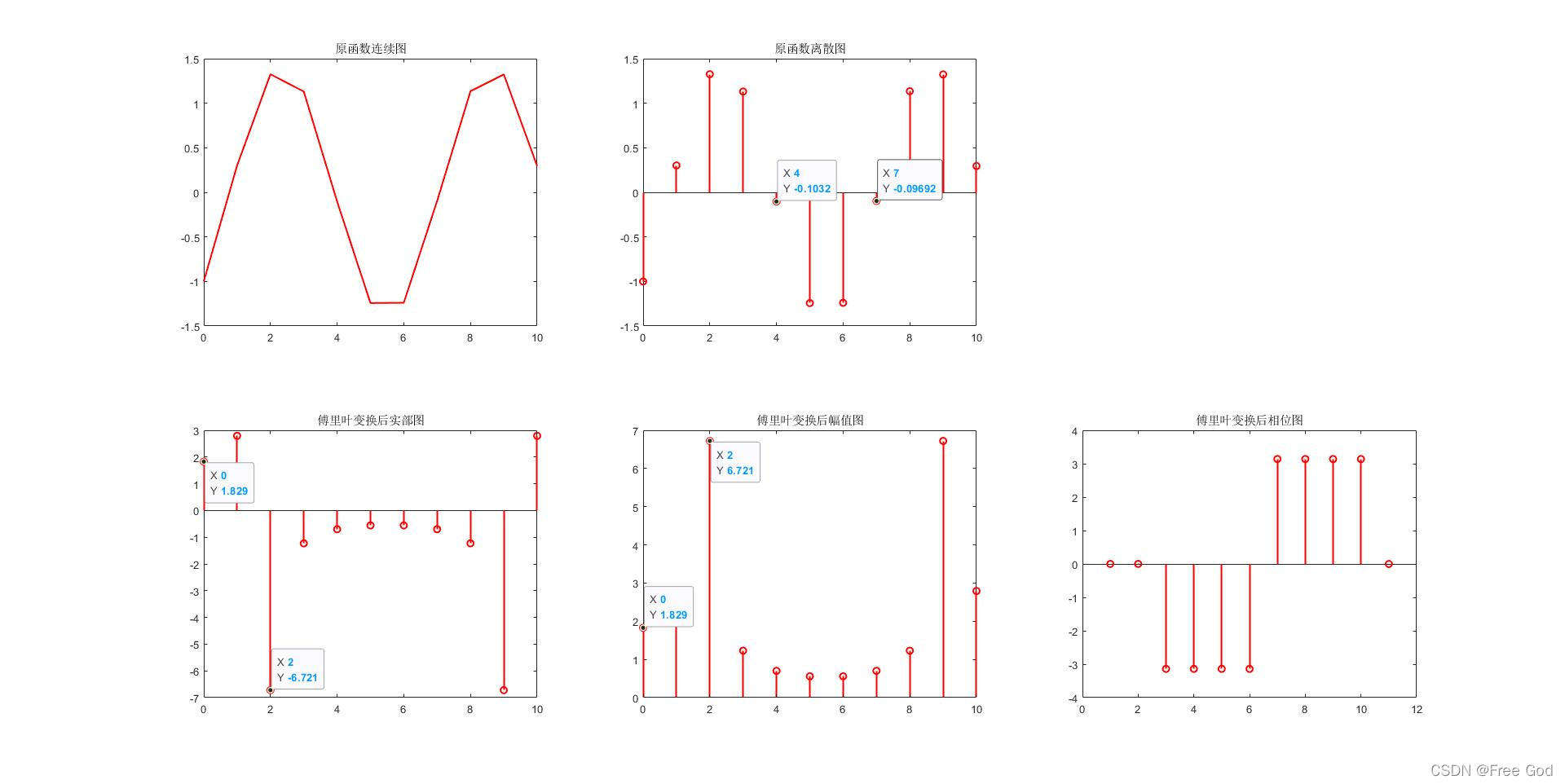
2、对 y = sin（x）进行离散傅里叶变换

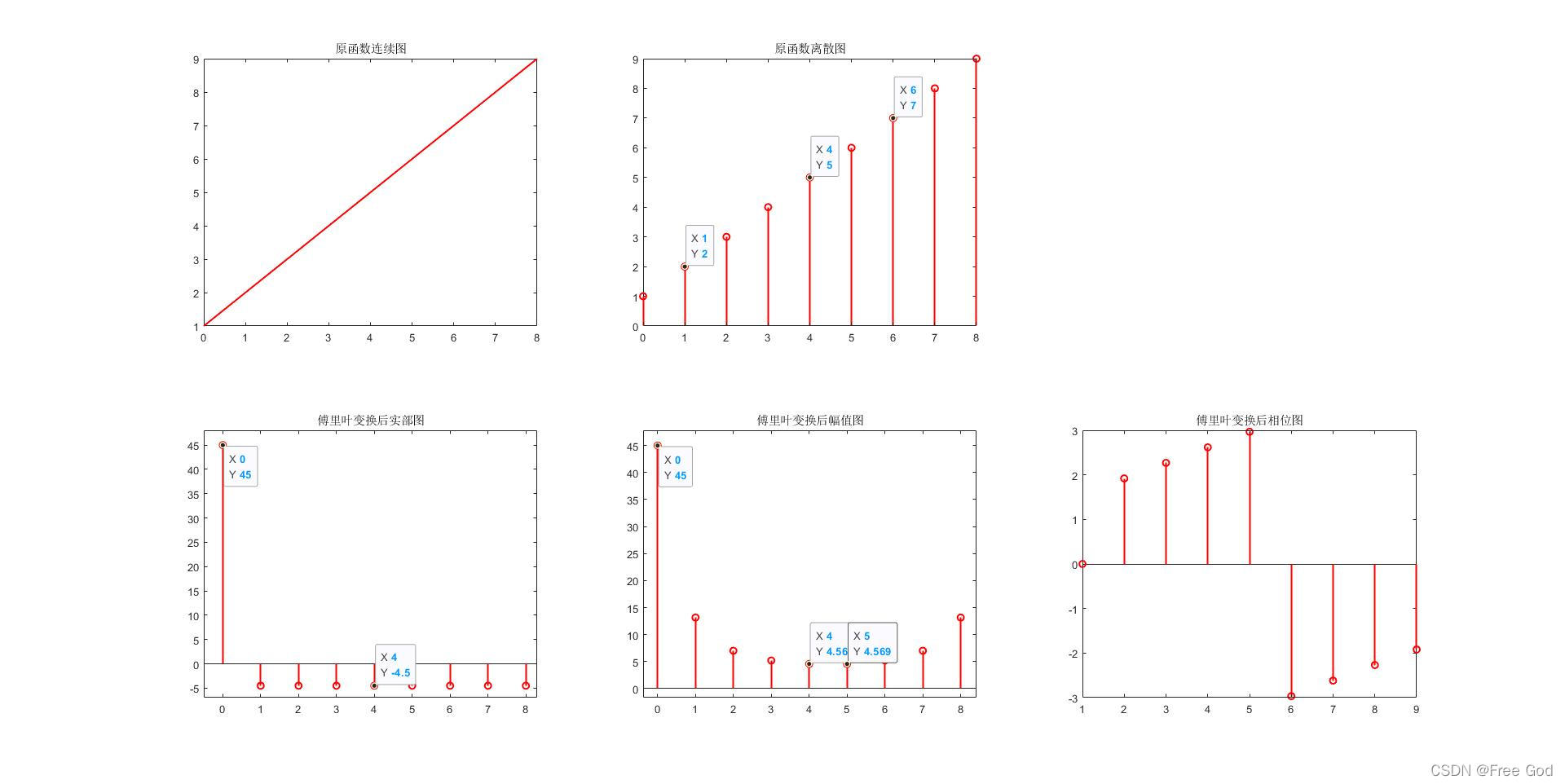
3、对 y = [1，2，4，5，6，7，8，9]进行傅里叶变换

4、对 y = sin（x）-cos（x）进行傅里叶变换

自写函数代码如下

function [fy,sumY] = Fourier2(y,dx,xLeft,xRight)
%一维离散傅里叶变换
%该函数是用于输入一个 函数 或 列向量 即y ，将y傅里叶变换后输出
%fy是y的离散傅里叶变换，sumY是fy的零频，即y的各个数相加
%此函数输出y傅里叶变换后的1、实部2、幅值3、相位

% 创建命名函数的函数句柄：
% fy = @myfun
% 创建匿名函数的函数句柄：
% fxy = @(x,y) x.^2 + y.^2;
if length(y) ==1
    x = xLeft:dx:xRight;
    y = y(x);
    fy = y;
else
    x = 0:1:length(y)-1;
end  
for x1 = 0:length(y)-1
   temp = 0;
   for x2 = 0:length(y)-1
       temp = temp + y(x2+1)*exp(-1j*2*pi*x1*x2/length(y));
   end
   fy(x1+1) = temp;
end
sumY = sum(y(:));
figure
subFigure = 3;
subplot(2,subFigure,1),plot(x,y,"red",'LineWidth',1.5),title("原函数连续图");
subplot(2,subFigure,2),stem(x,y,"red",'LineWidth',1.5),title("原函数离散图");
subplot(2,subFigure,4),stem(x,real(fy),"red",'LineWidth',1.5),title("傅里叶变换后实部图");
subplot(2,subFigure,5),stem(x,abs(fy),"red",'LineWidth',1.5),title("傅里叶变换后幅值图");
subplot(2,subFigure,6),stem(angle(fy),"red",'LineWidth',1.5),title("傅里叶变换后相位图");
end