sigmoid为什么会有梯度消失的问题

---

问题描述

sigmoid为什么会有梯度消失的问题？

---

Sigmoid函数是一种常见的激活函数，它的公式是：

Sigmoid函数的输出值域在(0, 1)之间，它可以将任意输入值映射到0和1之间。

Sigmoid函数的导数（或梯度）是：

这个导数公式是由链式法则推导出来的。首先，我们对sigma(z)求导：

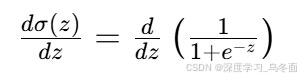
应用链式法则，我们得到：
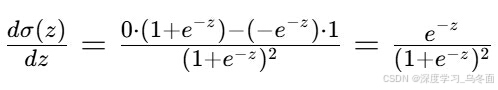然后，我们用\sigma(z)替换e^{-z}：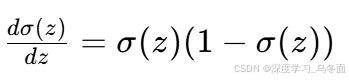

原因分析：

接下来，我们分析为什么Sigmoid函数会导致梯度消失问题。

当z的值很大或者很小的时候e^{-z}会变得非常小或者非常大，导致sigma(z)接近1或者0。当sigma(z)接近1或0时，sigma’(z)的值会非常小，接近0。这意味着在Sigmoid函数的输出接近1或0时，对于输入z的微小变化，输出的变化非常微小，即梯度非常小。

在神经网络中，梯度是用来更新权重的。如果梯度很小，那么权重的更新也会非常微小，这会导致网络在训练过程中收敛得非常慢。如果网络层次较多，每层的输出都会通过Sigmoid函数，那么梯度会在每一层都被缩小，最终导致梯度消失，即靠近输入层的梯度几乎为0，无法有效地更新网络的权重。

---

解决方案：

这就是Sigmoid函数导致梯度消失问题的原因。为了解决这个问题，可以使用其他激活函数，如ReLU（线性整流单元），它在正区间内的梯度是恒定的，可以缓解梯度消失问题。