Java基础09——选择排序和插入排序

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

思路如下：
n个记录的文件的直接选择排序可经过n-1趟直接选择排序得到有序结果：

1. 初始状态：无序区为R[1…n]，有序区为空。
2. 第1趟排序
   在无序区R[1…n]中选出关键字最小的记录R[k]，将它与无序区的第1个记录R[1]交换，使R[1…1]和R[2…n]分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。
   ……
3. 第i趟排序
   第i趟排序开始时，当前有序区和无序区分别为R[1…i-1]和R(i…n）。该趟排序从当前无序区中选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1…i]和R分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。
   
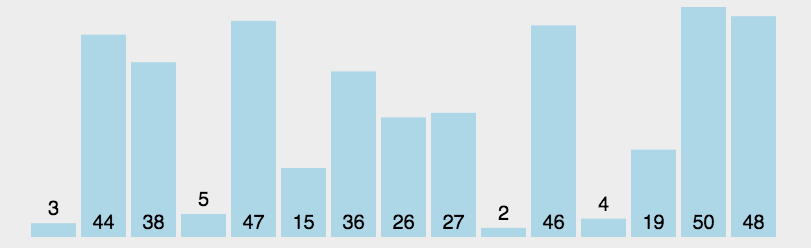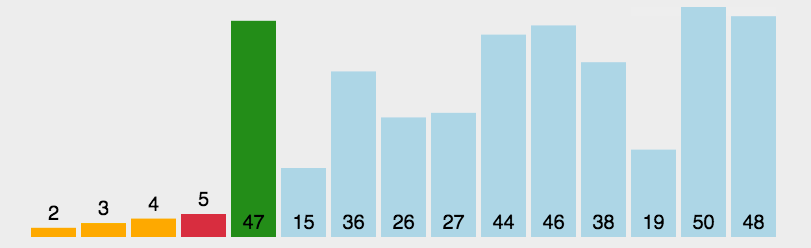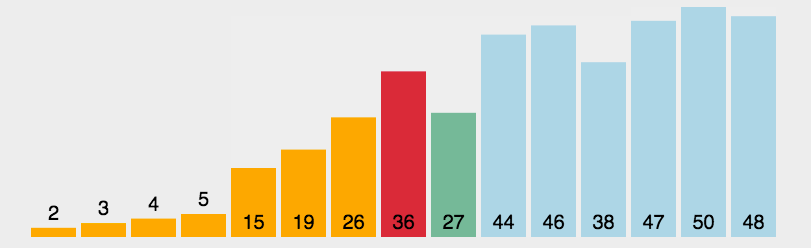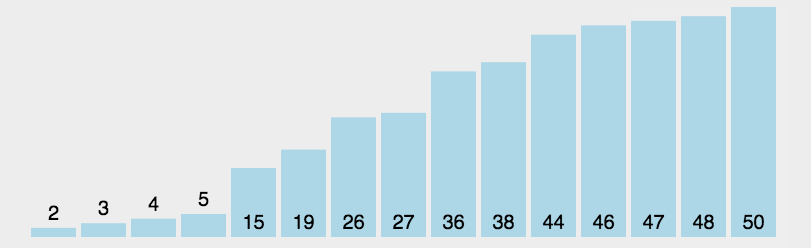
   流程图如下：
   
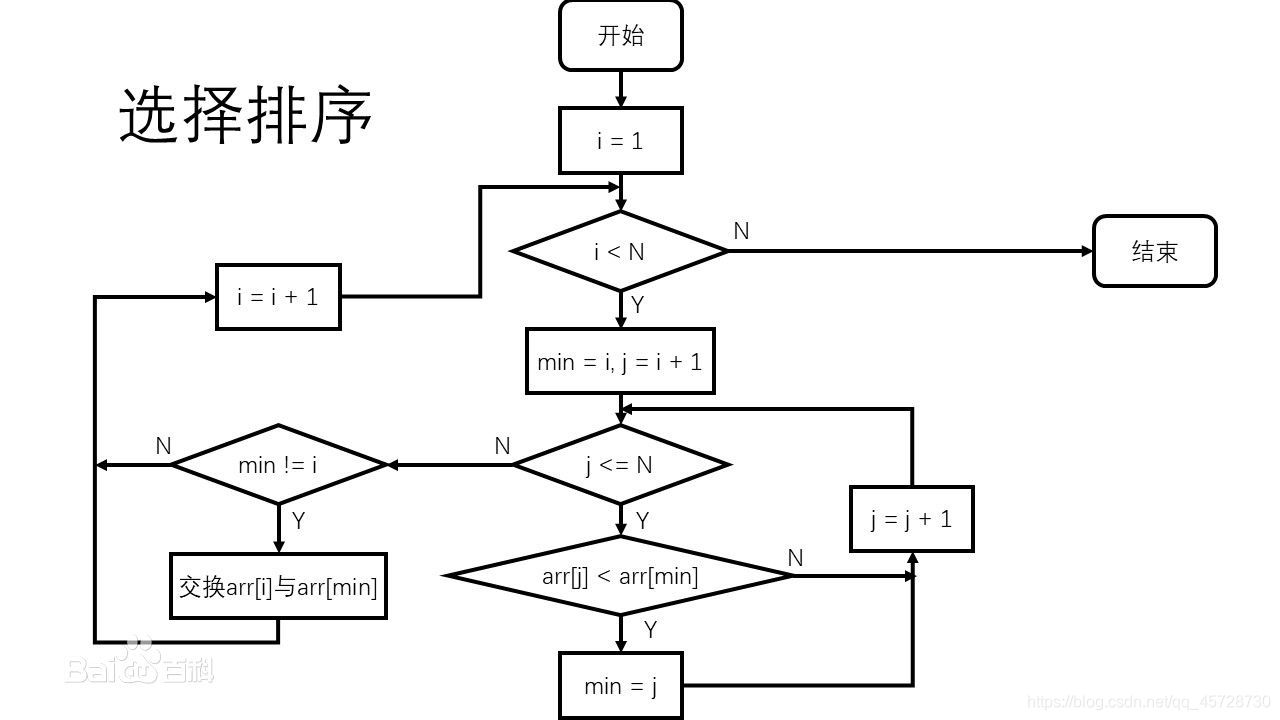
   代码如下：

public static void main(String[] args){
   //准备原始数据
   int[] a={98,65,32,95,62,86,53,76};
   //处理
   selectionSort(a);
 }
 //选择排序
 static void selectionSort(int[] a){
    for(int i=0;i<a.length;i++){
       int min=i;
       for(int j=i;j<a.length;j++){
          if(a[j]<a[min]){
             min=j;
             }
          }
          if(min!=i){
             int temp=a[min];
             a[min]=a[i];
             a[i]=temp;
          }
       }
  }

插入排序

插入排序（Insertion sort）是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序，这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据，算法适用于少量数据的排序，时间复杂度为O(n^2)。是稳定的排序方法。插入算法把要排序的数组分成两部分：第一部分包含了这个数组的所有元素，但将最后一个元素除外（让数组多一个空间才有插入的位置），而第二部分就只包含这一个元素（即待插入元素）。在第一部分排序完成后，再将这个最后元素插入到已排好序的第一部分中。

插入排序的基本思想是：每步将一个待排序的记录，按其关键码值的大小插入前面已经排序的文件中适当位置上，直到全部插入完为止。

思路如下：

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到下一位置中
6. 重复步骤2~5
   如果比较操作的代价比交换操作大的话，可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种，称为二分查找排序。

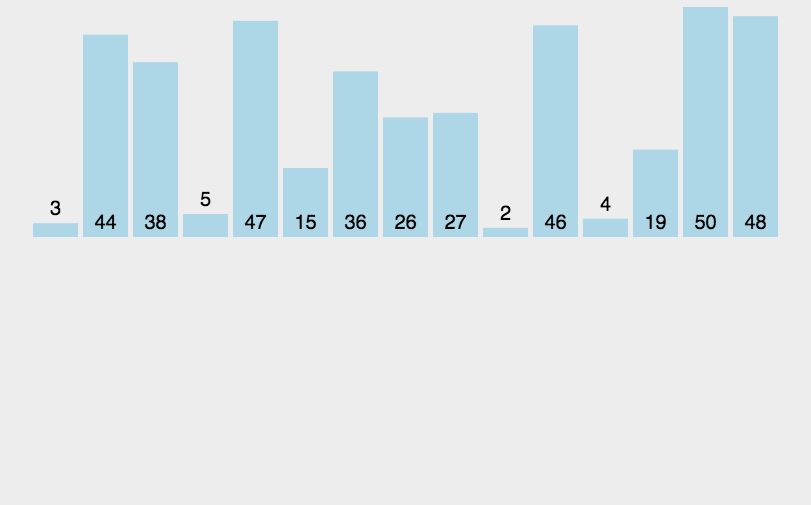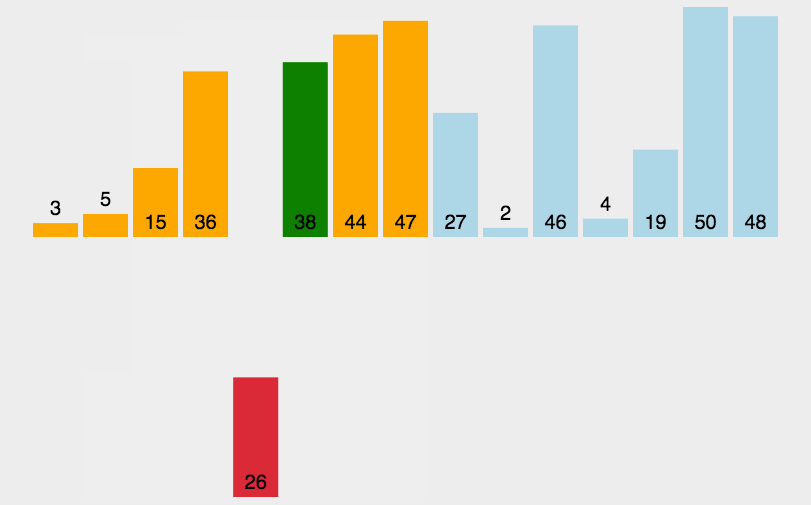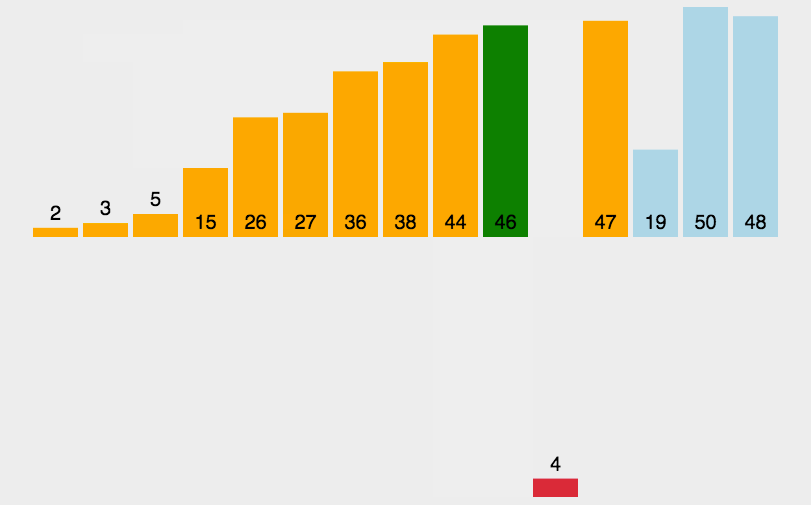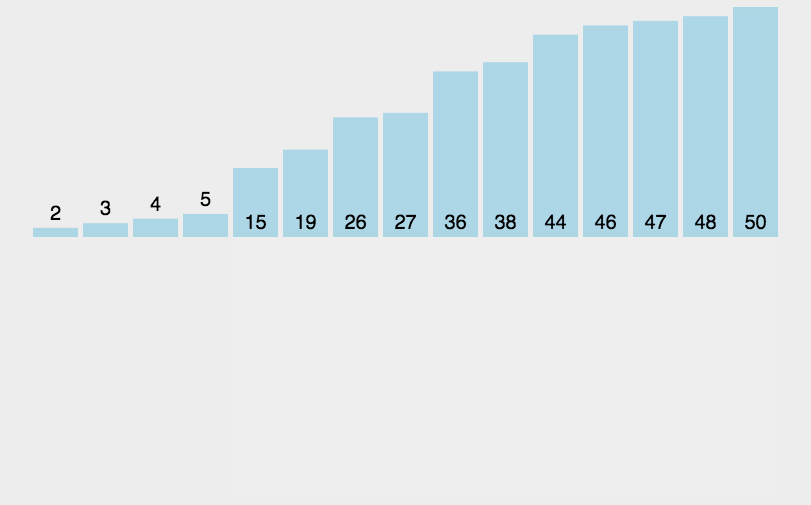
代码如下：

public static void main(String[] args){
//准备原始数据
   iny[] a={98,65,32,95,62,86,53,76};
//处理
   inserSort(a);
//插入排序
static void inserSort(int[] a){
   for(int i=0;i<a.length-1;i++){
      int x=a[i+1];
      int y=i;
      while(y>=0 && x<a[y]){
         a[y+1]=a[y];
         y--;
      }
      a[y+1]=x;
   }
}