计算机二级考试高频考点

计算机二级考点摘要

一.数据结构与算法
考点一
1.1 算法是对解题方案的准确而完整的描述，简单来说算法就是解决问题的操作步骤。
算法的基本特征:

1. 可行性
2. 确定性
3. 有穷性
4. 拥有足够的情报

1.2 算法的复杂度

1. 时间复杂度

2. 空间复杂度
   考点二：数据结构的基本概念
   2.1 什么是数据结构
   数据结构是指相互有关两的数据元素的集合。它包括俩个要素。即“数据”和“结构”。
   所谓数据就是处理数据元素的集合
   结构就是一种关系，集合元素之间的关系
   2.2 数据的结构表述
   数据的逻辑结构就是一个二元组：
   B=(D,R)
   B 表示数据结构，D是数据元素的集合，R是D上的关系的集合，它反映了D中个数据元素之前的关系，我们一般可以用一种树结构来表示。

   2.2节点的基本概念

3. 根节点

4. 终端节点

5. 内部节点

   2.3线性结构与非线性结构的区别

线性结构	有且只有一个根节点；每一个节点最多只有前件，也最多只有一个后件；
非线性结构	不满足上面条件的数据结构就是非线性结构；非线性结构主要是指树形结构和网状结构

考点三 线性表及其顺序的储存结构
1.线性表的基本概念
在数据结构中线性结构通常被称为线性表 ，线性表示最简单也是最常用的一种数据结构。
2.线性表的顺序结构
通常线性表尅采用顺序结构和链式储存俩种储存结构。
顺序表具有俩个特征

• 所有元素所占的储存空间是连续的。

• 数据元素在储存空间中是紧邻的，是按照逻辑顺序依次安放的
  考点四 栈与队列

• 栈的基本定义
  栈数据结构是一种特殊的线性表，它所有的插入语删除都限定在表的同一端进行，允许插入与删除的叫做栈顶，不允许插入的叫做栈底。
  当栈中没有元素时，称为空栈。

栈最重要的法则是，先进后出，后进先出。

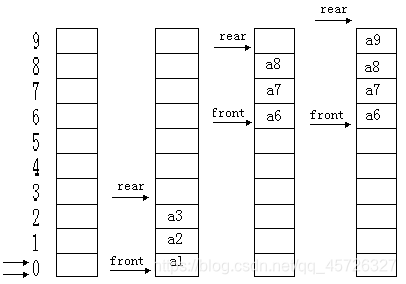
1. 队列的定义
   队列是允许在一段出入，再另端进行删除的线性表。
   记住一句话，先进先出，后进后出

2. 队列的运算
   队列的运算需要一个队头和一个队尾
   队头指针为front，队尾指针为rear。
   

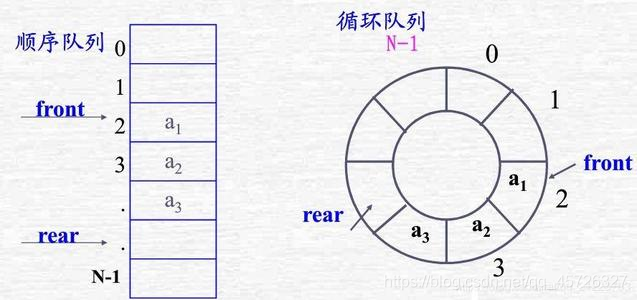
3. 循环队列的运算以及定义
   循环队列就是将队列的储存空间的最后一个位置绕到第一个位置，形成逻辑上的环状空间，供队列循环使用。
   

-关于循环队列

• 第一种情况
  当front<rear(队尾指针大于队首的时候)，这个时候的求元素为rear-front个

• 第二种情况
  当front>rear，元素为front-rear个

• 第三种情况
  front=rear的时候，队列要么为空，要么为满。
  考点5 线性链表

• 线性链表的基本概念：
  线性链表指线性表的链式储存结构，简称链表

• 线性链表的储存但愿是任意的，各数据节点的储存序号可以是连续的也可以是不连续的，各节点的存储空间的位置关系与逻辑关系的不一致。

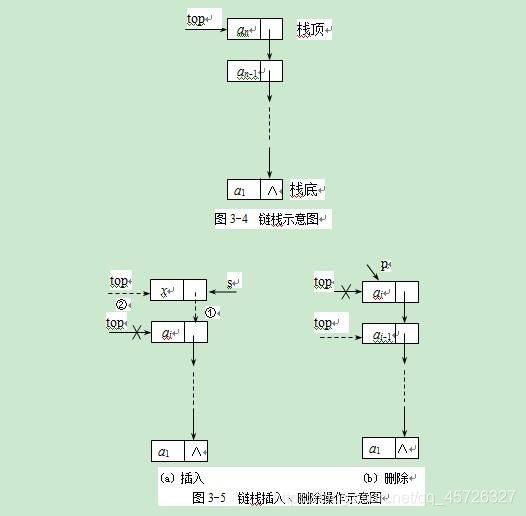
• 带链的栈

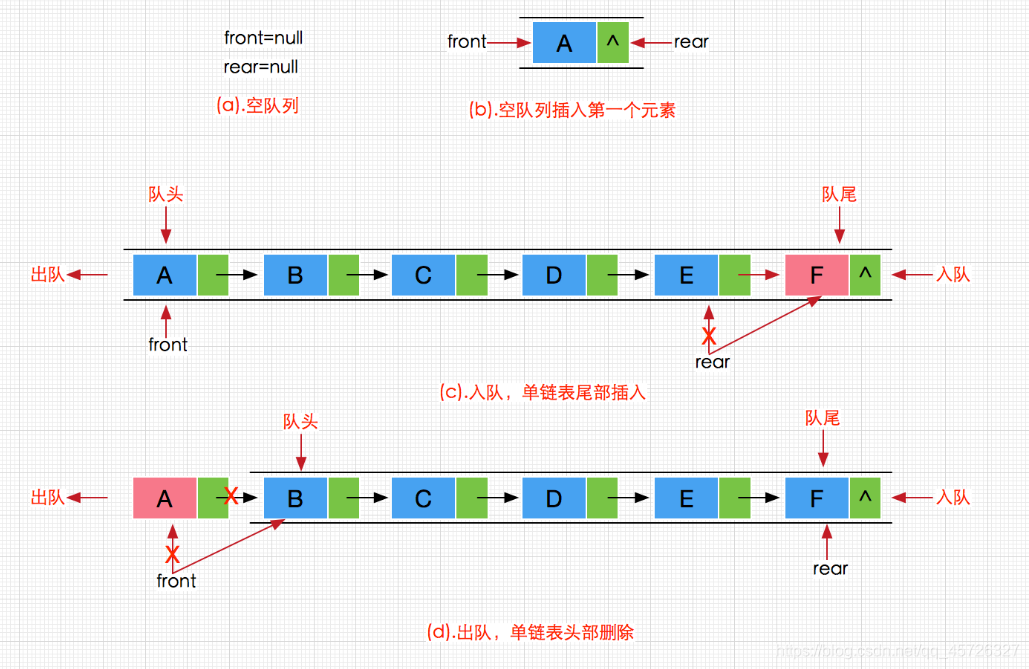
• 带链的队列
  

• 顺序表与链表的比较
  顺序表的优点：
  可以随机存取表中的任意节点。
  无须表示节点间的逻辑关系额外增加存储空间
  缺点：
  插入和删除的效率低
  顺序表的储存空间不易扩展
  顺序表不便于储存空间的动态分配

• 链表
  优点：
  在插入和删除运算时，只需要改变指针即可，不要移动元素。
  链表的储存空间易于扩充，方便空间的动态的分配、
  缺点：
  需要额外得到空间来表示数据之间的的逻辑关系 ，储存密度比顺序表低

• 循环链表
  

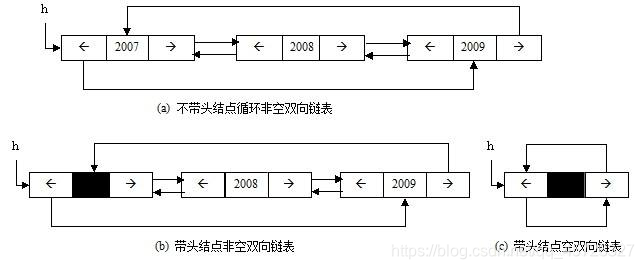
• 关于链表的运算
  栈为空时，头指针和尾指针都为nulll
  栈中只有一个元素时，头指针和尾指针都指向这个元素。
  top不等于botom，无法确定栈中拥有的元素。
  考点6 树与二叉树
  1.树的相关术语

• 父节点：根节点
  每一个节点只有一个前件

• 子节点和叶子节点
  没有后件的称为叶子节点

• 度
  一个节点所拥有的后件个数

• 深度
  树的最大层次称为树的深度。
  其他节点所在的层次等于他们的父节点加1

• 子树
  以一个子节点为根基构成的树，称为子树
  2.树的性质
  树的节点数等于数中所有节点的度之和再加1
  3.二叉树及其性质
  特点

• 二叉树可以为空

• 二叉树最多只有二棵子树，二叉树不存在大于2的节点

• 二叉树有左右之分

性质

• 二叉树的第k层上，最多有2^(k-1)个节点

• 深度为m的二叉树，最多有2^(m-1)个节点

• 对任何一个二叉树，度为0的节点，总是要比度为2的节点多一个

• 具有n个节点的二叉树，深度至少为，以2为底n为真数的大对数+1
  log2n+1，对数取整

• 满二叉树
  满二叉树是指最后一层外，每一层上的所有节点都是二个节点
  而满二叉树满足二叉树的所有特点

• 完全二叉树