Eigen小白学习笔记

于 2024-06-23 10:38:11 发布
阅读量143 收藏
点赞数 1
文章标签： 学习 笔记 c++ opencv
原文链接：https://blog.youkuaiyun.com/QLeelq/article/details/111599195
版权

该笔记学习链接：https://blog.youkuaiyun.com/QLeelq/article/details/111599195

1 Eigen框架

在这里插入图片描述

2 矩阵基础

2.1 矩阵和向量

矩阵 (Matrix)
矩阵是一个由数字排成矩形阵列的集合，每个数字称为矩阵的一个元素或项。矩阵的大小由其行数和列数决定，通常表示为m×n矩阵，其中m是行数，n是列数。

向量可以视为特殊形式的矩阵，即当矩阵的列数为1时，它是列向量；当行数为1时，它是行向量。因此，向量也可以参与矩阵运算。

Matrix<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>
  • scalar：矩阵的类型，包括float、double、int、复数float
  • RowsAtCompileTime：行数
  • ColsAtCompileTime：列数

matrix提供了丰富的矩阵类型，例如matrix4f，表示4*4的矩阵，如下：

typedef Matrix<float, 4, 4> Matrix4f;//4行4列，float

d”表示double类型，”f”表示float类型，”i”表示整数，”c”表示复数

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;


int main()
{
	Matrix4f fourf;
	fourf << 1.2, 2.5, 1.3, 2.1,
			2.2, 2.3, 2.4, 2.5,
			3.5, 3.6, 3.7, 3.8,
			4.2, 4.3, 4.4, 4.5;
	std::cout << "Here is the matrix f4:\n" << fourf << std::endl;
}

在这里插入图片描述
读取行和列的数量方法：

 int r = matrix.rows();//行
 int c = matrix.cols();//列
 //或者直接输出
 std::cout << "fourf rows is:\n" << fourf.rows() << std::endl;
std::cout << "fourf cols is:\n" << fourf.cols() << std::endl;

在这里插入图片描述

向量 (Vector)
向量是一个有方向和大小的量，可以用一组有序的数字来表示。在数学中，向量通常表示为一个列矩阵（即一个n×1的矩阵），其中的每个元素代表向量的一个分量。

typedef Matrix<float, 3, 1> Vector3f;//3行1列，float
typedef Matrix<int, 1, 2> RowVector2i;//1行，2列，int

2.2 动态矩阵

Eigen中除了定义上面固定大小的矩阵外，还有一种动态矩阵，也就是说编译的时候大小未知，在程序运行以后才确定大小。例如：

typedef Matrix<double, Dynamic, Dynamic> MatrixXd;//n行，n列。double类型矩阵。
typedef Matrix<int, Dynamic, 1> VectorXi;//动态列向量，n行1列
Matrix<float, 3, Dynamic>//3行n列

2.3 定义

定义前，在程序中添加eigen

using Eigen::MatrixXd;
using Eigen::Vector2d;
  • MatrixXf

MatrixXf 表示一个动态大小的浮点型矩阵。这里的“动态大小”意味着矩阵的行数和列数可以在运行时指定。

适用于任意大小的二维浮点数数组，非常适合处理大小不确定或需要灵活变化的矩阵运算。

  • VectorXf

VectorXf 是一个动态大小的浮点型向量。虽然它在内部也是一个矩阵，但默认被视作列向量（即一个n×1的矩阵）。

专门用于处理一维的浮点数序列，通常代表有方向的量或数据序列。

  • RowVectorXf

RowVectorXf 同样是动态大小的浮点型向量，但与VectorXf不同，它默认被视作行向量（即一个1×n的矩阵）。

当你需要处理一维数据，但逻辑上更倾向于将其视为一行时使用。尽管在数学运算上与列向量等效（通过转置），但在表达意图和代码可读性上有其独特价值。

2.3.1 未初始化类型

Matrix3f a;//3*3，固定大小float，未初始化
MatrixXf b;// n*n，动态大小float，未初始化
MatrixXf a(10,15);//10*15，动态大小float，未初始化
VectorXf b(30);//动态大小浮点型，30个元素，1*30，向量，未初始化

2.3.2 初始化类型

Matrix3f m;//3-by-3，float
m << 1, 2, 3,
     4, 5, 6,
     7, 8, 9;//不换行也行，只是为了看着方便，因为是行优先

2.3.3 使用已知来定义未知矩阵

例1：

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	RowVectorXd vec1(3);
	vec1 << 1, 2, 3;
	RowVectorXd vec2(4);
	vec2 << 1, 4, 9, 16;
	RowVectorXd joined(7);
	joined << vec1, vec2;
	std::cout << "Here is the vector v:\n" << joined << std::endl;
}

在这里插入图片描述
例2：

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	MatrixXf matA(2, 2);
	matA << 1, 2, 3, 4;
	MatrixXf matB(4, 4);
	matB << matA, matA / 10, matA / 10, matA;
	std::cout << "Here is the vector v:\n" << matB << std::endl;
}

在这里插入图片描述
例3：

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	Matrix3f m;
	m.row(0) << 1, 2, 3;
	m.block(1, 0, 2, 2) << 4, 5, 6, 7;
	//从（1,0）开始取（2,2）大小的块
	m.col(2).tail(2) << 8, 9;
	//从第二列结尾取两个
	std::cout << "Here is the result:\n" << m << std::endl;
}

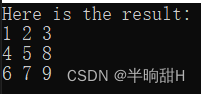
在这里插入图片描述
4位以内的向量还可以用下列方式进行定义并初始化：

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	Vector2d a(5.0, 6.0);
	Vector3d b(5.0, 6.0, 7.0);
	Vector4d c(5.0, 6.0, 7.0, 8.0);
	std::cout << "Here is the result:\n" << c << std::endl;
}

在这里插入图片描述

2.4 访问矩阵信息

2.4.1 获取矩阵元素

矩阵元素访问用(i,j)的形式，下标从0开始

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	MatrixXf m(2, 2);
	m<< 1, 2, 3, 4;  //1 2 3 4
	m(1, 0) = 6;   // 1 2 6 4
	m(1, 1) = 2.7;  //  1 2  6  2.7
	m(0, 1) = m(0, 0) + m(1, 0);  //  1 7  6  2.7
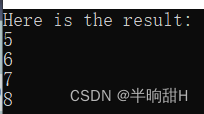
	std::cout << "Here is the result:\n" << m << std::endl;
	VectorXd v(2);
	v(0) = 2.3; 
	v(1) = v(0) - 1;
	std::cout << "Here is the result:\n" << v << std::endl;
}

在这里插入图片描述

2.4.2 rows()

返回矩阵的行数

 #include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	MatrixXf m(2, 2);
	m<< 1, 2, 3, 4;
	m(1, 0) = 6;
	m(1, 1) = 2.7;
	m(0, 1) = m(0, 0) + m(1, 0);
	std::cout << "Here is the result:\n" << m << std::endl;
	std::cout << "ROWS:\n" << m.rows() << std::endl;
	VectorXd v(2);
	v(0) = 2.3;
	v(1) = v(0) - 1;
	std::cout << "Here is the result:\n" << v << std::endl;
	std::cout << "ROWS:\n" << v.rows() << std::endl;
	RowVector2f R(2);
	R(0) = 1.1;
	R(1) = 2.2;
	std::cout << "Here is the result:\n" << R << std::endl;
	std::cout << "ROWS:\n" << R.rows() << std::endl;
}

在这里插入图片描述

2.4.3 cols()

此函数返回矩阵的列数

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	MatrixXf m(2, 2);
	m<< 1, 2, 3, 4;
	m(1, 0) = 6;
	m(1, 1) = 2.7;
	m(0, 1) = m(0, 0) + m(1, 0);
	std::cout << "Here is the result:\n" << m << std::endl;
	std::cout << "COLS:\n" << m.cols() << std::endl;
	VectorXd v(2);
	v(0) = 2.3;
	v(1) = v(0) - 1;
	std::cout << "Here is the result:\n" << v << std::endl;
	std::cout << "COLS:\n" << v.cols() << std::endl;
	RowVector2f R(2);
	R(0) = 1.1;
	R(1) = 2.2;
	std::cout << "Here is the result:\n" << R << std::endl;
	std::cout << "COLS:\n" << R.cols() << std::endl;
}

在这里插入图片描述

2.4.4 size()

对于动态大小的矩阵(MatrixXf)和向量(VectorXf、RowVectorXf)，size()函数返回的是矩阵或向量中元素的总数。

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	MatrixXf m(2, 2);
	m << 1, 2, 3, 4;
	m(1, 0) = 6;
	m(1, 1) = 2.7;
	m(0, 1) = m(0, 0) + m(1, 0);
	std::cout << "Here is the result:\n" << m << std::endl;
	std::cout << "SIZE:\n" << m.size() << std::endl;
	VectorXd v(2);
	v(0) = 2.3;
	v(1) = v(0) - 1;
	std::cout << "Here is the result:\n" << v << std::endl;
	std::cout << "SIZE:\n" << v.size() << std::endl;
	RowVector2f R(2);
	R(0) = 1.1;
	R(1) = 2.2;
	std::cout << "Here is the result:\n" << R << std::endl;
	std::cout << "SIZE:\n" << R.size() << std::endl;
}

在这里插入图片描述

2.5 重置矩阵大小

- resize()

resize() 是一个用于改变矩阵或向量尺寸的成员函数。这个函数允许你在运行时动态地调整已有对象的大小

固定大小对象注意事项：对于像Matrix3f这样的固定大小对象，你不能使用resize()来改变其尺寸，因为它们的尺寸在编译时就已经固定，试图调用resize()将会导致编译错误。

MatrixXf matrix(3, 4); // 初始为3x4的矩阵
matrix.resize(4, 5); // 调整为4x5的矩阵
VectorXf vector(10); // 初始长度为10的向量
vector.resize(15); // 调整为长度为15的向量

resize的大小发生改变的话会删除原来的值，相当于重新定义了一个矩阵。如果resize()的大小没有改变，则元素依旧保存。

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;
using Eigen::MatrixXd;
using Eigen::Vector2d;

int main()
{
	MatrixXf m(2, 2);
	m << 1, 2, 3, 4;
	m(1, 0) = 6;
	m(1, 1) = 2.7;
	m(0, 1) = m(0, 0) + m(1, 0);
	m.resize(2, 2);
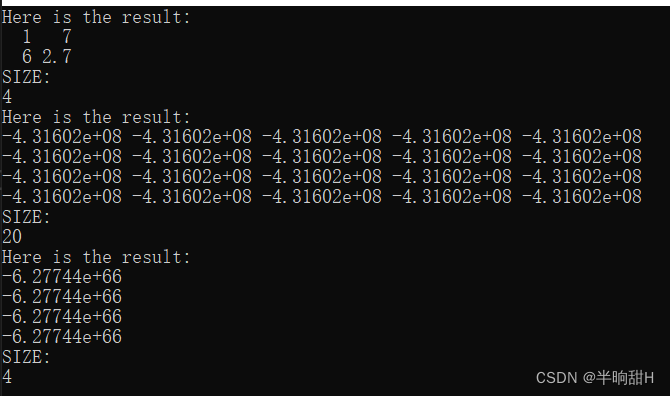
	std::cout << "Here is the result:\n" << m << std::endl;
	std::cout << "SIZE:\n" << m.size() << std::endl;
	m.resize(4, 5);
	std::cout << "Here is the result:\n" << m << std::endl;
	std::cout << "SIZE:\n" << m.size() << std::endl;
	
	VectorXd v(2);
	v(0) = 2.3;
	v(1) = v(0) - 1;
	v.resize(4);
	std::cout << "Here is the result:\n" << v << std::endl;
	std::cout << "SIZE:\n" << v.size() << std::endl;
}

在这里插入图片描述

  • “=”重置大小

对于动态矩阵可以通过赋值操作改变大小，但是固定矩阵则会报错。

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;

int main()
{
    MatrixXd a(3,3);
    MatrixXd b(2,2);
    b<<1,2,3,4;
    a = b;//a的大小也是(2,2)
    cout<<a<<endl;
}

在这里插入图片描述

2.6 怎么选择固定矩阵和动态矩阵

2.6.1 固定大小矩阵（如Matrix3f, Matrix4d等）

  • 定义明确：这类矩阵的行数和列数在编译时就已经确定，例如Matrix3f表示一个3x3的浮点数矩阵，Matrix4d表示一个4x4的双精度矩阵。
  • 性能优势：由于尺寸固定，编译器可以进行更多的优化，如栈上分配内存、避免运行时的尺寸检查和动态内存分配，从而提高运行效率。
  • 内存占用稳定：固定大小矩阵的内存占用在程序运行期间是固定的，有利于内存管理。
  • 限制：一旦定义，其大小不能在运行时更改。

2.6.2 动态大小矩阵（如MatrixXf, MatrixXd等）

  • 灵活性：动态大小矩阵在创建时或运行时可以指定其尺寸，如MatrixXf mat(3, 4);创建一个3x4的浮点数矩阵。这使得它们非常灵活，适用于大小未知或经常变化的场景。
  • 内存管理：动态矩阵可能在堆上分配内存，并且在尺寸改变时可能需要重新分配内存，这可能导致一定的性能开销。
  • 适应性强：适用于各种大小的矩阵操作，不需要为每一种可能的大小定义单独的变量类型。
  • 运行时尺寸检查：在某些操作中，动态矩阵会在运行时检查尺寸兼容性，这增加了安全性但可能略减性能。

当矩阵小于16的时候，建议使用固定矩阵。

3 矩阵的运算

3.1 加法和减法

  • 二元操作符+/-表示两矩阵相加：a+b
  • 一元操作符-表示对矩阵取负：-a
  • 组合操作法+=或者-=：a+=b
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;

int main()
{
  Matrix2d a;
  a << 1, 2,
       3, 4;
  MatrixXd b(2,2);
  b << 2, 3,
       1, 4;
  std::cout << "a + b =\n" << a + b << std::endl;
  std::cout << "a - b =\n" << a - b << std::endl;
  std::cout << "Doing a += b;" << std::endl;
  a += b;
  std::cout << "Now a =\n" << a << std::endl;
  Vector3d v(1,2,3);
  Vector3d w(1,0,0);
  std::cout << "-v + w - v =\n" << -v + w - v << std::endl;
}

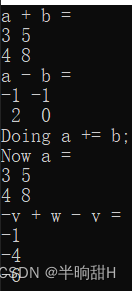
在这里插入图片描述

3.2 标量的乘除法

标量乘除法表示矩阵中的每个元素都对标量进行相应的运算。
#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;

int main()
{
  Matrix2d a;
  a << 1, 2,
       3, 4;
  Vector3d v(1,2,3);
  std::cout << "a * 2.5 =\n" << a * 2.5 << std::endl;
  std::cout << "0.1 * v =\n" << 0.1 * v << std::endl;
  std::cout << "Doing v *= 2;" << std::endl;
  v *= 2;
  std::cout << "Now v =\n" << v << std::endl;
}

在这里插入图片描述
在数学中转置矩阵、共轭矩阵、伴随矩阵分别表示为，

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;

int main()
{
  //MatrixXcf a = MatrixXcf::Random(2,2);//随机产生2-by-2的复数矩阵
  Matrix3d a;
  a<< 1,2,3,4,5,6,7,8,9;
  cout<<"矩阵a："<<endl<<a<<endl;
  cout<<"转置矩阵："<<endl<<a.transpose()<<endl;
  cout<<"共轭矩阵："<<endl<<a.conjugate()<<endl;
  cout<<"伴随矩阵："<<endl<<a.adjoint()<<endl;
  Matrix3d b;
  b = a.transpose();
  cout<<"矩阵a："<<endl<<a<<endl;
  cout<<"矩阵b："<<endl<<a<<endl;
}

在这里插入图片描述
伴随矩阵结果错的，原因：这个伴随是指共轭转置，对于实矩阵来说，共轭还是原矩阵，所以伴随等于转置

注意这里不能用自己的转置(或者其他操作)直接赋值给自己，例如下面的情况会报错：

a = a.transpose();//不允许

如果需要改变自己的状态，可以用transposeInPlace() ，adjointInPlace()来代替

a.transposeInPlace();//直接进行转置，但是也不允许用“=”给自己赋值

3.3 矩阵之间的乘法

矩阵与向量的相乘也是使用操作符*，共有 * 和*=两种操作符

#include <iostream>
#include <Eigen/Dense>

using namespace Eigen;
int main()
{
  Matrix2d mat;
  mat << 1, 2,
         3, 4;
  Vector2d u(-1,1), v(2,0);
  std::cout << "Here is mat*mat:\n" << mat*mat << std::endl;
  std::cout << "Here is mat*u:\n" << mat*u << std::endl;
  std::cout << "Here is u^T*mat:\n" << u.transpose()*mat << std::endl;
  std::cout << "Here is u^T*v:\n" << u.transpose()*v << std::endl;
  std::cout << "Here is u*v^T:\n" << u*v.transpose() << std::endl;
  std::cout << "Let's multiply mat by itself" << std::endl;
  mat = mat*mat;//这个操作是允许的
  std::cout << "Now mat is mat:\n" << mat << std::endl;
}

在这里插入图片描述

3.5 矩阵的点乘与叉乘

3.5.1 点乘

点乘，也叫数量积。结果是一个向量在另一个向量方向上投影的长度，是一个标量。
假设向量a和向量b:
在这里插入图片描述
则a和b的点积公式（要求一维向量a和向量b的行列数相同）为：
在这里插入图片描述

3.5.2 叉乘

两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量，并且两个向量的叉积与这两个向量组成的坐标平面垂直。
设向量a和向量b：
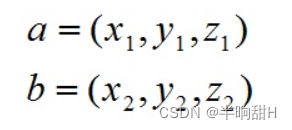
在这里插入图片描述
a和b的叉乘公式为，其中i = （1,0,0）、 j = （0,1,0）、k = （0,0,1）：

在这里插入图片描述
根据i、j、k间关系，有：
在这里插入图片描述
在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面

3.5.3 点乘和叉乘的使用

点乘与叉乘使用dot()和cross()操作完成。

#include <iostream>
#include <Eigen/Dense>
 
using namespace Eigen;
using namespace std;
int main()
{
  Vector3d v(1,2,3);
  Vector3d w(0,1,2);
 
  cout << "Dot product: " << v.dot(w) << endl;
  double dp = v.adjoint()*w; // automatic conversion of the inner product to a scalar
  cout << "Dot product via a matrix product: " << dp << endl;
  cout << "Cross product:\n" << v.cross(w) << endl;
}

在这里插入图片描述

3.6 基本算数运算

#include <iostream>
#include <Eigen/Dense>

using namespace std;
int main()
{
	Eigen::Matrix2d mat;
	mat << 1, 2,
		3, 4;
	cout << "Here is mat.sum():       " << mat.sum() << endl;//求和
	cout << "Here is mat.prod():      " << mat.prod() << endl;//求积
	cout << "Here is mat.mean():      " << mat.mean() << endl;//求平均值
	cout << "Here is mat.minCoeff():  " << mat.minCoeff() << endl;//求最小值
	cout << "Here is mat.maxCoeff():  " << mat.maxCoeff() << endl;//求最大值
	cout << "Here is mat.trace():     " << mat.trace() << endl;//迹，也就是对角线的和
	cout << "Here is mat.diagonal():\n " << mat.diagonal() << endl;
	cout << "Here is mat.diagonal().sum():     " << mat.diagonal().sum() << endl;//迹
}

在这里插入图片描述
最大值和最小值还可以返回他们相应的坐标：

#include <iostream>
#include <Eigen/Dense>
using namespace Eigen;
using namespace std;

int main()
{
	Eigen::Matrix2d m;
	m << 2, 5,
		1, 4;
	std::ptrdiff_t i, j;
	float minOfM = m.minCoeff(&i, &j);
	cout << "Here is the matrix m:\n" << m << endl;
	cout << "Its minimum coefficient (" << minOfM
		<< ") is at position (" << i << "," << j << ")\n\n";
	RowVector4f v;
	v << 1, 2,3,4;
	int maxOfV = v.maxCoeff(&i);
	cout << "Here is the vector v: " << v << endl;
	cout << "Its maximum coefficient (" << maxOfV
		<< ") is at position " << i << endl;
	
}

std::ptrdiff_t 是C++标准库中的一种数据类型，它用来表示两个指针之间的距离，即两个指针可以指向的元素的数量。
由于坐标从0开始，所以V的最大值在3
在这里插入图片描述

4 矩阵的块操作

块操作是以矩形的形式对矩阵或者数组进行操作。块操作可以作为左值也可以作为右值。

4.1 块操作的使用

块操作对静态、动态矩阵或者数组都可以使用。

块操作有两种使用方式，其中块的起始位置为（i,j）块大小为 (p,q)。也就是说从i开始取p个元素，从j开始取q个元素。

matrix.block(i,j,p,q);
matrix.block<p,q>(i,j);

例1：

#include <Eigen/Dense>
#include <iostream>

using namespace std;

int main()
{
	Eigen::MatrixXf m(4, 4);
	m << 1, 2, 3, 4,
		5, 6, 7, 8,
		9, 10, 11, 12,
		13, 14, 15, 16;
	cout << "Block in the middle" << endl;
	cout << m.block<2, 2>(1, 1) << endl << endl;//从（1,1）位置取大小为（2,2）的块
	for (int i = 1; i <= 3; ++i)
	{
		cout << "Block of size " << i << "x" << i << endl;
		cout << m.block(0, 0, i, i) << endl << endl;//从（0,0）位置取大小为（i,i）的块
	}
}

在这里插入图片描述
例2：

#include <Eigen/Dense>
#include <iostream>
using namespace std;
using namespace Eigen;
int main()
{
	Array22f m;
	m << 1, 2,
		3, 4;
	Array44f a = Array44f::Constant(0.6);//4×4数组的每一项都赋0.6
	cout << "Here is the array a:" << endl << a << endl << endl;
	a.block<2, 2>(1, 1) = m;//把m赋值给a(1,1)开始的（2,2）大小的块
	cout << "Here is now a with m copied into its central 2x2 block:" << endl << a << endl << endl;
	a.block(0, 0, 2, 3) = a.block(2, 1, 2, 3);//a（2,1）开始的（2,3）大小的块赋值给a(0,0)开始的（2,3）大小的块
	cout << "Here is now a with bottom-right 2x3 block copied into top-left 2x3 block:" << endl << a << endl << endl;
}

在这里插入图片描述

4.2块的行操作和列操作

  • 行操作：第i行，matrix.row(i)
  • 列操作：第j列，matrix.col(j)
#include <Eigen/Dense>
#include <iostream>
using namespace std;

int main()
{
	Eigen::MatrixXf m(3, 3);
	m << 1, 2, 3,
		4, 5, 6,
		7, 8, 9;
	cout << "Here is the matrix m:" << endl << m << endl;
	cout << "2nd Row: " << m.row(1) << endl;
	m.col(2) += 3 * m.col(0);//第0列的3倍，加到第2列上
	cout << "After adding 3 times the first column into the third column, the matrix m is:\n";
	cout << m << endl;
}

在这里插入图片描述

4.3 矩阵的角操作

Eigen可以对一些特殊的角块进行操作：
在这里插入图片描述

#include <Eigen/Dense>
#include <iostream>
using namespace std;
int main()
{
	Eigen::Matrix4f m;
	m << 1, 2, 3, 4,
		5, 6, 7, 8,
		9, 10, 11, 12,
		13, 14, 15, 16;
	cout << "m.leftCols(2) =" << endl << m.leftCols(2) << endl << endl;//左边两列
	cout << "m.bottomRows<2>() =" << endl << m.bottomRows<2>() << endl << endl;//底下两行
	m.topLeftCorner(1, 3) = m.bottomRightCorner(3, 1).transpose();
	//右下角的块大小为3行1列（8,12,16），转置到左上角去
	cout << "After assignment, m = " << endl << m << endl;
}

在这里插入图片描述

4.4 对向量进行块操作

Eigen对一维向量或者一维数组进行操作：

在这里插入图片描述

#include <Eigen/Dense>
#include <iostream>

using namespace std;

int main()
{
  Eigen::ArrayXf v(6);//6个元素的数组
  v << 1, 2, 3, 4, 5, 6;
  cout << "v.head(3) =" << endl << v.head(3) << endl << endl;//头部的3个元素块
  cout << "v.tail<3>() = " << endl << v.tail<3>() << endl << endl;//尾部的3个元素块
  v.segment(1,4) *= 2;//从第1个开始的4个元素块，然后对它的子块进行乘以2倍的操作。
  cout << "after 'v.segment(1,4) *= 2', v =" << endl << v << endl;
}

在这里插入图片描述
转载链接：https://blog.youkuaiyun.com/QLeelq/article/details/111599195

半晌甜H
关注
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值