PAT-A 1123 Is It a Complete AVL Tree (30 分)

AVL树是一种自平衡二叉搜索树。

在AVL树中，任何节点的两个子树的高度最多相差 1 个。

如果某个时间，某节点的两个子树之间的高度差超过 1，则将通过树旋转进行重新平衡以恢复此属性。

图 1−4 说明了旋转规则。

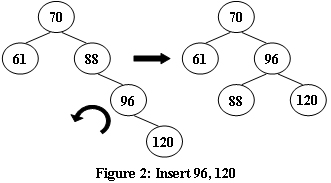
现在，给定插入序列，请你输出得到的AVL树的层序遍历，并判断它是否是完全二叉树。

输入格式
第一行包含整数 N，表示插入序列中元素个数。

第二行包含 N 个不同的整数表示插入序列。

输出格式
第一行输出得到的AVL树的层序遍历序列。

第二行，如果该AVL树是完全二叉树，则输出 YES，否则输出 NO。

数据范围
1≤N≤20
输入样例1：
5
88 70 61 63 65
输出样例1：
70 63 88 61 65
YES
输入样例2：
8
88 70 61 96 120 90 65 68
输出样例2：
88 65 96 61 70 90 120 68
NO

#include <bits/stdc++.h>

using namespace std;
struct node
{
    int data;
    struct node*l,*r;
};
int flag=1;
int n;
int shendu(struct node*root)
{
    int l1,l2;
    if(root)
    {
        l1 = shendu(root->l);
        l2 = shendu(root->r);
        return max(l1,l2)+1;
    }
    return 0;
}
struct node*ll(struct node*root)
{
    struct node*p;
    p=root->l;
    root->l = p->r;
    p->r = root;
    return p;
}
struct node*rr(struct node*root)
{
    struct node*p=root->r;
    root->r = p->l;
    p->l = root;
    return p;
}
struct node*lr(struct node*root)
{
    root->l = rr(root->l);
    root = ll(root);
    return root;
}
struct node*rl(struct node*root)
{
    root->r = ll(root->r);
    root = rr(root);
    return root;
}
void create(int shu,struct node*&root)
{
    if(root==NULL)
    {
        root = new node;
        root->data=shu;
        root->l = NULL;
        root->r = NULL;
    }
    else if(shu<root->data)
    create(shu,root->l);
    else
    create(shu,root->r);
    if(shendu(root->l)-shendu(root->r)>1)
    {
        if(shendu(root->l->l)>shendu(root->l->r))
        root = ll(root);
        else
        root = lr(root);
    }
    else if(shendu(root->r)-shendu(root->l)>1)
    {
        if(shendu(root->r->r)>shendu(root->r->l))
        root = rr(root);
        else
        root = rl(root);
    }
    return;
}
bool check(queue<node*> q)
{
    while(!q.empty())
    {
        node* now = q.front();
        q.pop();
        if(now!=NULL)
        return false;
    }
    return true;
}
void cengxv(struct node*root)
{
    queue<node*> q;
    q.push(root);
    while(!q.empty())
    {
        node* now  = q.front(); 
        q.pop();
        if(now!=NULL)
        {
            cout <<now->data<<" ";
            q.push(now->l);
            q.push(now->r);
        }
        else 
        {
            if(!check(q))
            flag=0;
        }
      
    }
}

int main()
{
    cin >> n;
    struct node*root=NULL;
    for(int i=1;i<=n;i++)
    {
        int x;
        cin >>x;
        create(x,root);
    }
    cengxv(root);
    cout <<endl;
    if(flag)
    cout <<"YES"<<endl;
    else
    cout <<"NO"<<endl;
    
    return  0;
}