葡萄酒质量数据集
葡萄酒质量数据集包括两个文件——红葡萄酒文件和白葡萄酒文件。红葡萄酒文件中包含1599条观测,白葡萄酒文件包含4898条观测。两个文件中都有1个输出变量和11个输入变量。输出变量是酒的质量,是一个从0(低质量)到10(高质量)的评分。输入变量是葡萄酒的物理化学成分和特性,包括非挥发性酸、挥发性酸、柠檬酸、残余糖分、氯化物、游离二氧化硫、总二氧化硫、密度、pH值、硫酸盐和酒精含量。
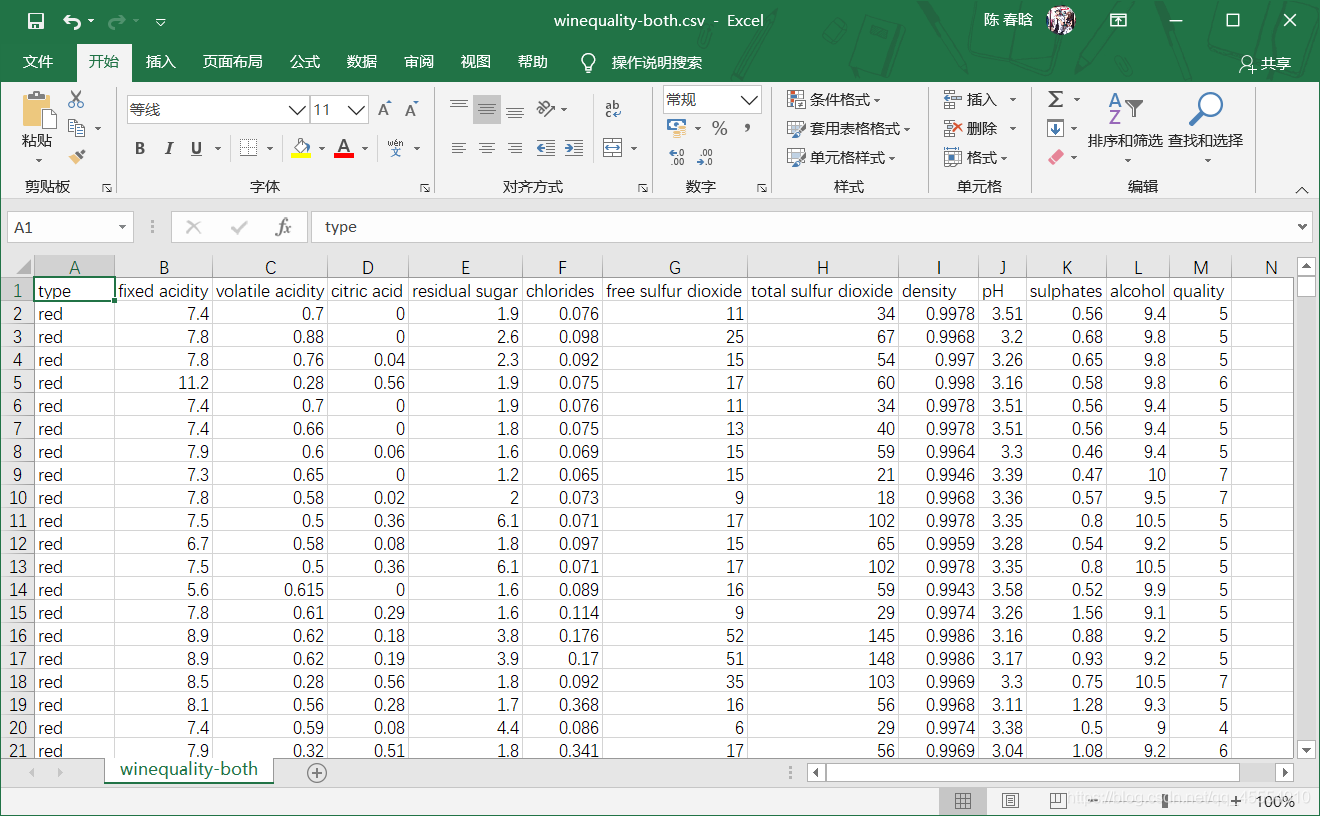
我们把这两个数据集合成一个数据集,保存在文件winequality-both.csv中。这个数据集中应该包括一个标题行和6497条。另外,还应该再添加一列,用来区分这行数据是红葡萄酒还是白葡萄酒的数据。
想要下载数据集?点我!
描述性统计
我们来对这个数据集进行分析。首先,我们要计算出每列的总体描述性统计量、质量列中的唯一值以及和这个唯一值对应的观测数量。代码如下:
#!/usr/bin/env python3
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.formula.api import ols, glm
# 将数据集读入到pandas数据框中
wine = pd.read_csv('winequality-both.csv', sep=',', header=0)
wine.columns = wine.columns.str.replace(' ', '_')
print(wine.head())
# 显示所有变量的描述性统计量
print(wine.describe())
# 找出唯一值
print(sorted(wine.quality.unique()))
# 计算值的频率
print(wine.quality.value_counts())
在使用pandas模块的read_csv()方法将文本文件读入一个pandas数据框之后,我们使用head()函数检查一下标题行和前五行数据,确保数据被正确加载。第17行代码使用pandas的describe()函数打印出数据集中每个数值型变量的摘要统计量。第20行代码使用unique()识别出质量列中的唯一值,并以升序打印在屏幕上。最后,第23行代码计算出质量列中每个唯一值在数据集中出现的次数,并把它们以降序打印到屏幕上。
这段代码的运行结果如下:
type fixed_acidity volatile_acidity ... sulphates alcohol quality
0 red 7.4 0.70 ... 0.56 9.4 5
1 red 7.8 0.88 ... 0.68 9.8 5
2 red 7.8 0.76 ... 0.65 9.8 5
3 red 11.2 0.28 ... 0.58 9.8 6
4 red 7.4 0.70 ... 0.56 9.4 5
[5 rows x 13 columns]
fixed_acidity volatile_acidity ... alcohol quality
count 6497.000000 6497.000000 ... 6497.000000 6497.000000
mean 7.215307 0.339666 ... 10.491801 5.818378
std 1.296434 0.164636 ... 1.192712 0.873255
min 3.800000 0.080000 ... 8.000000 3.000000
25% 6.400000 0.230000 ... 9.500000 5.000000
50% 7.000000 0.290000 ... 10.300000 6.000000
75% 7.700000 0.400000 ... 11.300000 6.000000
max 15.900000 1.580000 ... 14.900000 9.000000
[8 rows x 12 columns]
[3, 4, 5, 6, 7, 8, 9]
6 2836
5 2138
7 1079
4 216
8 193
3 30
9 5
Name: quality, dtype: int64
输出显示,质量评分中有6497个观测,评分范围从3到9,平均质量评分为5.8,标准差为0.87;质量列中的唯一值是3、4、5、6、7、8和9;有2836个观测的质量评分为6,2138个观测的质量评分为5,1079个观测的质量评分为7,216个观测的质量评分为4,193个观测的质量评分为8,30个观测的质量评分为3,5个观测的质量评分为9。
分组、直方图与t检验
下面我们分别分析红葡萄酒数据和白葡萄酒数据,看看统计量是否会保持不变。
...
# 按照葡萄酒类型显示质量的描述性统计量
print(wine.groupby('type')[['quality']].describe().unstack('type'))
# 按照葡萄酒类型显示质量的特定分位数值
print(wine.groupby('type')[['quality']].quantile([0.25, 0.75]).unstack('type'))
# 按照葡萄酒类型查看质量分布
red_wine = wine.loc[wine['type'] == 'red', 'quality']
white_wine = wine.loc[wine['type'] == 'white', 'quality']
sns.set_style("dark")
print(sns.distplot(red_wine, norm_hist=True, kde=False, color="red", label="Red wine"))
print(sns.distplot(white_wine, norm_hist=True, kde=False, color="white", label="White wine"))
sns.utils.axlabel("Quality Score", "Density")
plt.title("Distribution of Quality by Wine Type")
plt.legend()
plt.show()
# 检验红葡萄酒和白葡萄酒的平均质量是否有所不同
print(wine.groupby(['type'])[['quality']].agg(['std']))
tstat, pvalue, df = sm.stats.ttest_ind(red_wine, white_wine)
print('tstat: %.3f pvalue: %.4f' % (tstat, pvalue))
groupby()函数使用type列中的两个值将数据分为两组。方括号可以生成一个列表,列表中的元素是用来生成输出的列。在这里我们只对质量列应用describe()函数。这些命令的结果就是生成一列统计量,来自红葡萄酒数据的计算结果和白葡萄酒数据的计算结果是相互垂直地堆叠在一起的。unstack()函数将结果重新排列,这样红葡萄酒和白葡萄酒的统计量就会显示在并排的两列中。quantile()函数对质量列计算第25百分位数和第75百分位数。
接下来,我们使用seaborn创建直方图,红条表示红葡萄酒,白条表示白葡萄酒。因为白葡萄酒数据比红葡萄酒多,所以直方图显示密度分布而不是频率分布。
最后,进行一下t检验,判断红葡萄酒和白葡萄酒的平均评分是否有区别。在这里我们想知道红葡萄酒和白葡萄酒评分的标准差是否相同,所以在t检验中可以使用合并方差。
下面是这段代码的运行结果。
type
quality count red 1599.000000
white 4898.000000
mean red 5.636023
white 5.877909
std red 0.807569
white 0.885639
min red 3.000000
white 3.000000
25% red 5.000000
white 5.000000
50% red 6.000000
white 6.000000
75% red 6.000000
white 6.000000
max red 8.000000
white 9.000000
dtype: float64
quality
type red white
0.25 5.0 5.0
0.75 6.0 6.0
AxesSubplot(0.125,0.11;0.775x0.77)
AxesSubplot(0.125,0.11;0.775x0.77)
quality
std
type
red 0.807569
white 0.885639
tstat: -9.686 pvalue: 0.0000

由绘制的密度分布直方图和输出结果可以得出结论:两种葡萄酒的评分都近似正态分布;t检验统计量为-9.686,p值为0.000,这说明白葡萄酒的平均质量评分在统计意义上大于红葡萄酒的平均质量评分。
成对变量之间的关系和相关性
前面已经检查了输出变量,下面简单研究一下输入变量。让我们计算一下输入变量两两之间的相关性,并为一些输入变量创建带有回归直线的散点图:
...
# 计算所有变量的相关矩阵
print(wine.corr())
# 从红葡萄酒和白葡萄酒的数据中取出一个“小”样本来进行绘图
def take_sample(data_frame, replace=False, n=200):
return data_frame.loc[np.random.choice(data_frame.index, replace=replace, size=n)]
reds_sample = take_sample(wine.loc[wine['type'] == 'red', :])
whites_sample = take_sample(wine.loc[wine['type'] == 'white', :])
wine_sample = pd.concat([reds_sample, whites_sample])
wine['in_sample'] = np.where(wine.index.isin(wine_sample.index), 1., 0.)
print(pd.crosstab(wine.in_sample, wine.type, margins=True))
# 查看成对变量之间的关系
sns.set_style("dark")
g = sns.pairplot(wine_sample, kind='reg', plot_kws={"ci": False, "x_jitter": 0.25, "y_jitter": 0.25}, hue='type',
diag_kind='hist', diag_kws={"bins": 10, "alpha": 1.0}, palette=dict(red="red", white="white"),
markers=["o", "s"], vars=['quality', 'alcohol', 'residual_sugar'])
print(g)
plt.suptitle('Histograms and Scatter Plots of Quality, Alcohol, and Residual Sugar', fontsize=14,
horizontalalignment='center', verticalalignment='top', x=0.5, y=0.999)
plt.show()
corr()函数可以计算出数据集中所有变量两两之间的线性相关性。
数据集中有6000多个点,所以如果将它们都画在统计图中,就很难分辨出清楚的点。我们定义了一个函数take_sample(),用来抽取在统计图中使用的样本点。这个函数使用pandas数据框索引和numpy的random.choice()函数随机选择一个行的子集。我们是用这个函数对红葡萄酒和白葡萄酒分别进行抽样,并将抽样所得的两个数据框连接成一个数据框。然后,在wine数据框中创建一个新列in_sample,并使用numpy的where()函数和pandas的isin()函数对这个新列进行填充,填充的值根据此行的索引值是否在抽样数据的索引值中分别设为1和0.最后,我们使用pandas的crosstab()函数来确认in_sample列中包含400个1(200条红葡萄酒数据和200条白葡萄酒数据)和6097个0。
seaborn的pairplot()函数可以创建一个统计图矩阵。主对角线上的图以直方图或密度图的形式显示了每个变量的单变量分布,对角线之外的图以散点图的形式显示了每两个变量之间的双变量分布,散点图中可以有回归直线,也可以没有。因为质量评分都是整数,所以加上一点振动可以更容易看出数据在何处集中。
这段代码的运行结果如下:
fixed_acidity volatile_acidity ... alcohol quality
fixed_acidity 1.000000 0.219008 ... -0.095452 -0.076743
volatile_acidity 0.219008 1.000000 ... -0.037640 -0.265699
citric_acid 0.324436 -0.377981 ... -0.010493 0.085532
residual_sugar -0.111981 -0.196011 ... -0.359415 -0.036980
chlorides 0.298195 0.







 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








