SVM简介详细推导核函数线性可分非线性可分-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_45523675/article/details/137276036

注意：由于该文章由jupyter nbconvert导出，若单独执行代码可能出现变量找不到或者没有导入库的情况，正确的做法是将所有的代码片段按顺序放到一个.py文件里面或者按顺序放入一个.ipynb文件的多个代码块中。

SVM(Support Vector Machine)

Vapnik发明用于解决二分类问题的机器学习算法。

线性可分与非线性可分

在二维平面中，线性可分指的是可以通过一条直线对平面上的点进行划分使得标签相同的点在直线的同一侧，标签不同的点在直线的不同侧。

在二维平面中，非线性可分则是指除去线性可分的情况。

下面是一个线性可分的例子：

import matplotlib.pyplot as plot
from random import random
x1 = []
x2 = []
y1 = []
y2 = []
figSize = (6, 6)
dotNum = 20
for i in range(dotNum):
    x1.append(random() * 1 + 4.5 - 0.5)
    x2.append(random() * 1 + 4.5 + 0.5)
    y1.append(x1[-1] + random() * 1 + 0.5)
    y2.append(x2[-1] - random() * 1 - 0.5)

fig, ax = plot.subplots(figsize = figSize)
ax.axis([3.5, 6.5, 2, 8])
ax.plot(x1, y1, "x")
ax.plot(x2, y2, "o")
ax.plot([3, 7], [3, 7], linewidth = 1)
ax.plot([3, 7], [2, 8], linewidth = 1)
ax.plot([3, 7], [1, 9], linewidth = 1)

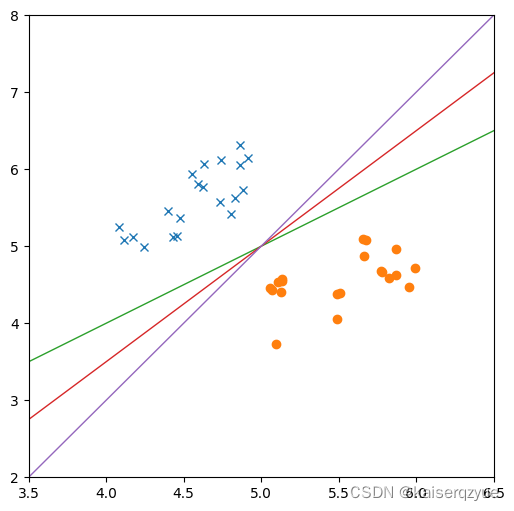
在这里插入图片描述

下面是一个非线性可分的例子：

import numpy as np
plot.close()
dotNum = 50
x1 = np.random.rand(dotNum) * 2 - np.ones(dotNum)
x2 = np.random.rand(dotNum) - 0.5 * np.ones(dotNum)
y1 = np.append(np.sqrt(1 - x1 ** 2), -1 * np.sqrt(1 - x1 ** 2))
x1 = np.append(x1, x1)
y2 = np.append(np.sqrt(0.25 - x2 ** 2), -1 * np.sqrt(0.25 - x2 ** 2))
x2 = np.append(x2, x2)
fig, ax = plot.subplots(figsize=figSize)
ax.axis([-1.5, 1.5, -1.5, 1.5])
ax.plot(x1, y1, "x")
ax.plot(x2, y2, "o")

在这里插入图片描述

问题引入

对于一个线性可分的数据集，存在着多条线段均可以达到划分数据集的目的，哪条直线的分类效果最好？

要找到最好，我们首先要知道什么叫做好。

Vapnik定义了性能指标：间隔。

一些定义

数据集：输入 $X=[x_1, x_2, ..., x_n]$ ，输出 $Y=[y_1, y_2, ..., y_n], y_i\in\{-1, 1\}$ 。
支持向量：将划分线分别向两侧平移后首次经过的数据向量集合。
间隔：将划分线分别向两侧移动至首次经过数据时，移动后形成的两条线之间的距离。
线性模型： $W^Tx+b=0$
线性可分： $\exists W, b$ 使得 $y_i(W^Tx_i+b)\ge0,\quad 1\le i \le n, i \in Z$

在下图中，上下两侧经过的点是支持向量，而上下两条直线之间的距离即间隔。

Vapnik认为间隔越大的直线越能够抵抗噪声的影响，因此Vapnik希望在能够划分数据集的直线中找到使间隔最大的那一条。

从下图中我们不难发现间隔最大的直线有无数条，而这无数条直线中我们只需要找到支持向量到直线距离相同的那一条（即中间那条直线）即可，这样能够尽可能的区分两类样本。

plot.close()
x1 = []
x2 = []
y1 = []
y2 = []
dotNum = 20
for i in range(dotNum):
    x1.append(random() * 1 + 4.5 - 0.5)
    x2.append(random() * 1 + 4.5 + 0.5)
    y1.append(x1[-1] + random() * 1 + 0.5)
    y2.append(x2[-1] - random() * 1 - 0.5)
line1X = [3, 7]
line1Y = [2, 8]
def dotDis2Line(dot, line):
    a = (line[1][1] - line[1][0]) / (line[0][1] - line[0][0])
    b = -1
    c = a * (-line[0][0]) + line[1][0]
    return np.abs(a * dot[0] + b * dot[1] + c) / np.sqrt(a ** 2 + b ** 2)
def moveDis2Dot(x, y, line):   
    d = -1
    for i in range(len(x)):
        if d == -1 or d > dotDis2Line([x[i], y[i]], line):
            d = dotDis2Line([x[i], y[i]], line)
    return d
d1 = moveDis2Dot(x1, y1, [line1X, line1Y])
d2 = moveDis2Dot(x2, y2, [line1X, line1Y])
print(d1, d2)
line2X = line1X
line2Y = line1Y + d1 / ((line1X[1] - line1X[0]) / (np.sqrt((line1X[1] - line1X[0]) ** 2 + (line1Y[1] - line1Y[0]) ** 2)))
line3X = line1X
line3Y = line1Y - d2 / ((line1X[1] - line1X[0]) / (np.sqrt((line1X[1] - line1X[0]) ** 2 + (line1Y[1] - line1Y[0]) ** 2)))
fig, ax = plot.subplots(figsize=figSize)
ax.axis([3.5, 6.5, 2, 8])
ax.plot(x1, y1, "x")
ax.plot(x2, y2, "o")
ax.plot(line1X, line1Y, linewidth = 1)
ax.plot(line2X, line2Y, linewidth = 1)
ax.plot(line3X, line3Y, linewidth = 1)

在这里插入图片描述

SVM的数学推导

复习两条知识：

$W^Tx+b=0$ 与 $aW^Tx+ab=0, \forall a\ne0$ 为同一个（超）平面
欧式空间中点到（超）平面（直线）的距离： $\frac{\vert W^Tx+b\vert}{\parallel W\parallel}$

有了上面的知识我们便可以写出SVM的数学模型：
$max\quad d = \frac{\vert W^Tx_i+b\vert}{\parallel W\parallel},\quad x_i\ is\ SV\quad s.t.\\ y_i(W^Tx_i+b)\ge0,\quad 1\le i \le n, i \in Z\\ W^Tx_i = W^Tx_j,\quad x_i\ and\ x_j\ are\ any\ SV$
上面的式子并不简单，因为我们不能很好的确定那些向量是支持向量。

不过，对于任何一个线性模型，我们总可以用 $a$ 去放缩支持向量到线性模型的距离，也就是： $\exists a, a\vert W^Tx_i+b\vert=1,\quad x_i\ is\ SV$ 。

而 $W^Tx+b=0$ 与 $aW^Tx+ab=0, \forall a\ne0$ 为同一个（超）平面（直线），我们只需要求出 $aW^Tx+ab=0, \forall a\ne0$ 即可。因此，我们可以对上面的式子进行如下整理：
$min\quad \frac 1 2{\parallel W\parallel}^2\quad s.t.\\ y_i(W^Tx_i+b)\ge1,\quad 1\le i \le n, i \in Z\\$
上面的优化问题显然是一个凸优化，可以通过最优化理论学习到的知识找到最优解。