题目描述:207. 课程表 - 力扣(LeetCode)
你这个学期必须选修 nnumCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
隐藏条件:nnumCourses 为总数,只需要判断是否存在环
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]] 输出:true 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]] 输出:false 解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
解题思路:
广度优先(BFS)
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] indegree= new int[numCourses]; //判断每门课的入度情况
Map<Integer,List<Integer>> map= new HashMap<>();//存储每门课后续的出度连接
for(int[] p :prerequisites){ //p[1] 前向
//构建邻接表
if(map.containsKey(p[1])){
map.get(p[1]).add(p[0]);
}else{
List<Integer> l1 = new ArrayList<>();
l1.add(p[0]);
map.put(p[1],l1);
}
indegree[p[0]]++;//入度数
}
Queue<Integer> queue = new LinkedList<>();
//入度为0的入队
for(int i=0;i<numCourses;i++){
if(indegree[i]==0){
queue.offer(i);
}
}
while (!queue.isEmpty()){
int k=queue.poll(); //取出入度为0的
if(map.containsKey(k)){
List<Integer> l1 = map.get(k);
for(Integer i : l1){
indegree[i]--;//将前序课程为k的课程入度减一
if(indegree[i]==0){ //入度数为0,则入队列
queue.offer(i);
}
}
map.remove(k);//将邻接表中所有以k出的线删除
}
}
if(map.isEmpty()){
return true;
}
return false;
}
}
优化:
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
// 入度数组
int[] indegree = new int[numCourses];
// 邻接表
List<List<Integer>> graph = new ArrayList<>();
for(int i = 0; i < numCourses; i++){
graph.add(new ArrayList<>());
}
// 构建图 + 入度统计
for(int[] p : prerequisites){
int course = p[0]; // 需要学的课
int pre = p[1]; // 前置课
graph.get(pre).add(course);
indegree[course]++;
}
// 队列:存所有入度为 0 的课
Queue<Integer> queue = new LinkedList<>();
for(int i = 0; i < numCourses; i++){
if(indegree[i] == 0){
queue.offer(i);
}
}
// 统计被学习的课程数
int count = 0;
// BFS
while(!queue.isEmpty()){
int cur = queue.poll();
count++;
for(int next : graph.get(cur)){
if(--indegree[next] == 0){
queue.offer(next);
}
}
}
// 如果学习的课数 == 总课程数 → OK
return count == numCourses;
}
}
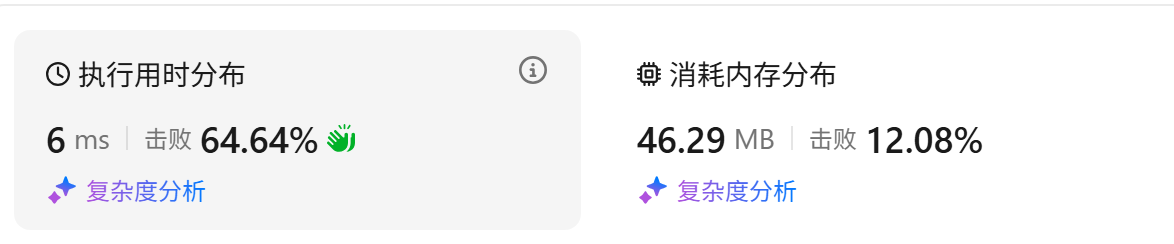
深度优先(DFS):
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<List<Integer>> list = new ArrayList<>(); //存储邻接图
int[] visit = new int[numCourses];//0表示未访问 1正在访问 2访问完成
for(int i=0;i<numCourses;i++){
list.add(new ArrayList<Integer>()); //
}
for(int[] p:prerequisites){ //p[0] p[1]为先修课
list.get(p[1]).add(p[0]);
}
for(int i=0;i<numCourses;i++){
if(!dfs(visit,list,i)){
return false;
}
}
return true;
}
public boolean dfs(int[] visit, List<List<Integer>> list,int cur){
if(visit[cur]==1){ //这是正在访问的,形成了环
return false;
}
if(visit[cur]==2){ //已经访问过
return true;
}
visit[cur] = 1; //进入递归
for(Integer k:list.get(cur)){//
if(!dfs(visit,list,k)){
return false;
}
}
visit[cur]=2;
return true;
}
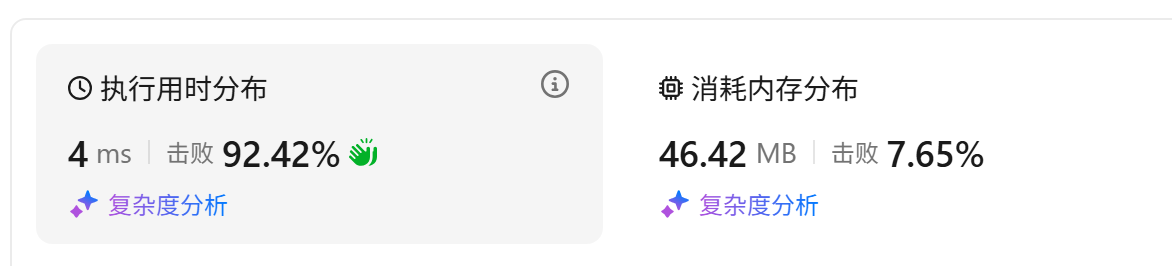
}





















 290
290

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








