对称密码体制:加密密钥与解密秘钥相同的密码体制,这种体制只要加密(或解密)算法,就可以反推出解密(或加密)算法
对称密码体制可以分为分组密码和流密码
古典密码是现代密码的基础,包含着密码处理的基本单元,历史上经典的对称密码体制都采用了替代、置换
替代:将明文中每个元素映射为另一个元素(可以看成是一个大的查表运算),明文元素被其他元素所替代而形成密文
置换:换位,改变明文消息中各元素的排列位置,但明文消息元素本身的取值或内容不变。
近现代密码技术常将替代和置换两种技术结合起来一起使用,使得密码很难破解
接下来是介绍几种有代表性的古典密码及加密运算思想,以及一些破译方法
- 移位密码
移位密码是一种简单的一种密码体制,也称凯撒密码,移位密码将英文字母向前移动k位,假设k=3,则密文字母与明文有如下关系:
明文:y 0 u t h
密文:b r x w k(将明文每个字母前移3位)
移位密码的明文空间(M)、密文空间(C)、秘钥空间(Km)都满足Z26,就表示模26的余数集合
加密变换:Ek(m)=m+(kmod26) m属于M,k属于K
解密变换:Dk(c) =c-(kmod26) c属于C,k属于K
缺点:利用穷举法可以将密文解密
轮转可以很好解密密文
- 一般单表替代密码
一般单表替代密码是通过建立一张“明文-密文”对照表来实现加密方法,这样明文消息中每个字母就不是移动相同的位数,而是根据某张字符对照表进行替换
| 明文 | a | b | c |
|---|---|---|---|
| 密文 | q | w | e |
这样可以很好的解决破译者使用枚举方法进行破解
但是破译者可以通过统计分析来破解
- 仿射密码
仿射密码对移位密码是一种改进,明文空间和密文空间与移位密码相同,但秘钥空间K={(k1,k2)|k1,k2属于Z26,gcd(k,26)=1}
c=Ek(m)=(k1m+k2)mod26
m=Dk(c )=k1^-1(c-k2)mod26
k1k1^-1=1mod26
在抗枚举攻击方面比移位密码要好一点 - 秘钥短语密码
秘钥短语密码选用一个英文短语或单词串作为秘钥,先去掉其中重复的字母,得到一个无重复的字母字符串,然后再将英文字母表中的其他字母依次写于该字母串后,就可以构造出一个字母代替表。

移位密码、一般单表替代密码、仿射密码、秘钥短语密码都属于单表替代密码
单表替代密码:明文字符和密文字符是一对一的映射关系
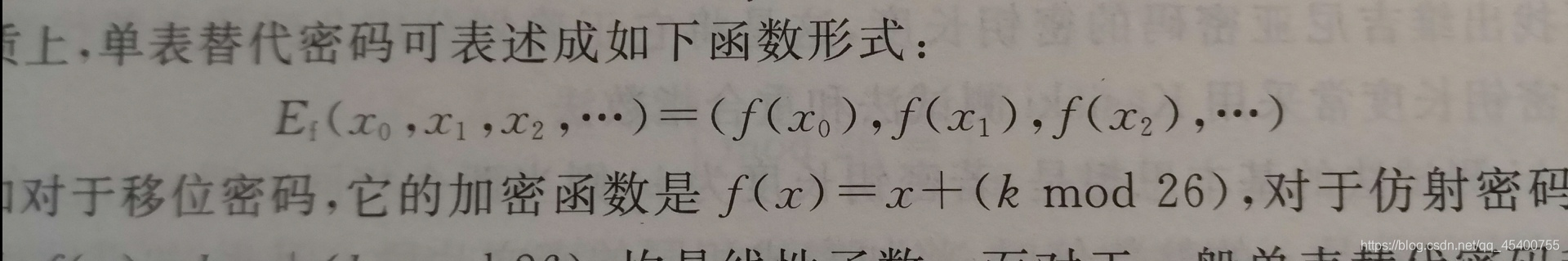
- 维吉尼亚密码
改密码体制有一个参数n,表示采用n位长度的字符串(例如一个英文单词)作为秘钥。在加解密时,同样把英文字母映射成0~25的数字在进行运算,并按n个字母一组进行变换。明文空间、密文空间、秘钥空间都是长度为n的英文字母串的集合。

破解维吉尼亚密码的基本思想:分解为多个单表替代密码组合,再分别统计分析就可以轻松破解,也不能抵抗明文攻击
- 希尔密码
利用矩阵进行加密
设明文对应的数字为7、8、11、11,密文对应的数字为1、3、1、4

- 置换密码
变换明文中各元素的对应位置(即对各元素换位),但保持其内容不变的方法。即通过对明文元素的重新排列来达到隐藏明文原始内容所表达含义的加密方法方法
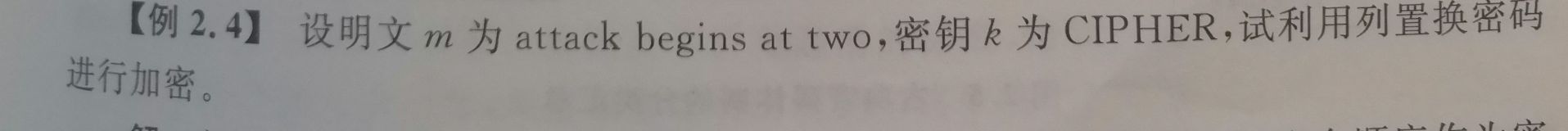
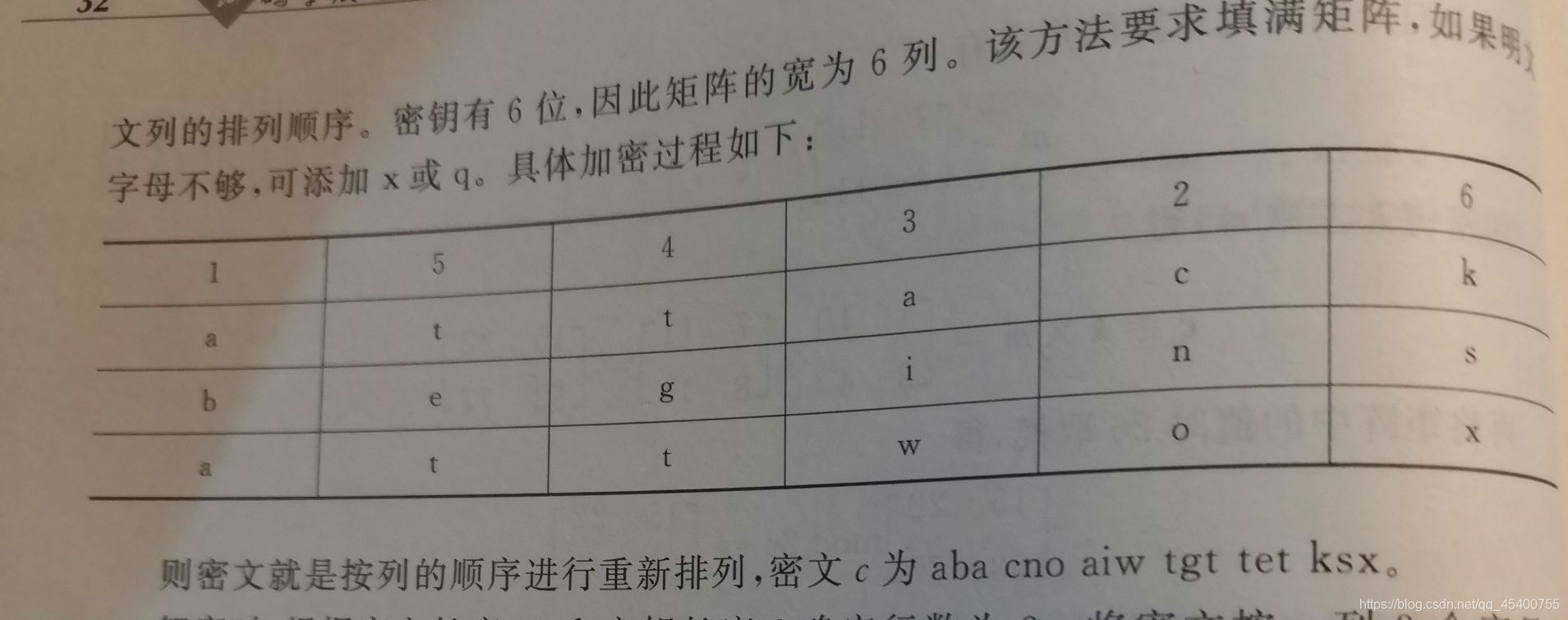
维吉尼亚密码、希尔密码都是多表替代密码,使用从明文到密文多个映射来隐藏单字母出现的频率。多表替代密码将明文字母串划分成为长度相同的消息单元,称为明文分组。对明文分组进行成组的替代,即使用了多张字母替代表
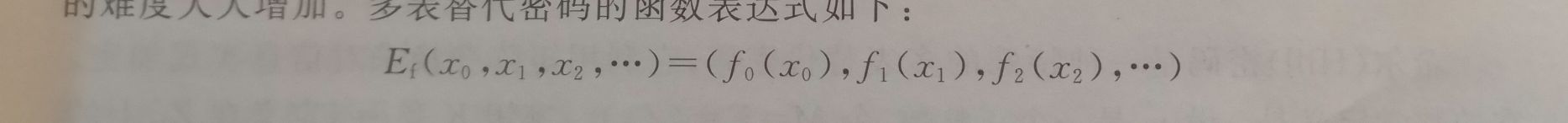








 本文深入探讨了对称密码体制,包括分组密码和流密码。介绍了古典密码如移位密码、一般单表替代密码、仿射密码、秘钥短语密码的原理和加密思想,以及它们的破解方法。同时,讨论了更复杂的维吉尼亚密码和希尔密码,这些属于多表替代密码,利用多张字母替代表隐藏明文信息。虽然对称密码体制在加密效率上有优势,但其主要缺点是密钥管理困难,容易受到统计分析攻击。
本文深入探讨了对称密码体制,包括分组密码和流密码。介绍了古典密码如移位密码、一般单表替代密码、仿射密码、秘钥短语密码的原理和加密思想,以及它们的破解方法。同时,讨论了更复杂的维吉尼亚密码和希尔密码,这些属于多表替代密码,利用多张字母替代表隐藏明文信息。虽然对称密码体制在加密效率上有优势,但其主要缺点是密钥管理困难,容易受到统计分析攻击。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








