文章目录
第二章 高级语言及其语法描述
上下文无关文法
例2.1 教材P30

例2.2 教材P30

例2.3 教材P30

最左推导、最右推导
最左推导:任何一步 α ⇒ β \alpha\Rightarrow\beta α⇒β都是对 α \alpha α中的最左非终结符进行替换
最右推导:任何一步 α ⇒ β \alpha\Rightarrow\beta α⇒β都是对 α \alpha α中的最右非终结符进行替换
最左推导
E + E ⇒ i + E ⇒ i + i E+E \Rightarrow i+E \Rightarrow i+i E+E⇒i+E⇒i+i
E ⇒ ( E ) ⇒ ( E + E ) ⇒ ( E ∗ E + E ) ⇒ ( i ∗ E + E ) ⇒ ( i ∗ i + E ) ⇒ ( i ∗ i + i ) E \Rightarrow (E) \Rightarrow (E+E) \Rightarrow (E*E+E) \Rightarrow (i*E+E) \Rightarrow (i*i+E) \Rightarrow (i*i+i) E⇒(E)⇒(E+E)⇒(E∗E+E)⇒(i∗E+E)⇒(i∗i+E)⇒(i∗i+i)
最右推导
E + E ⇒ E + i ⇒ i + i E+E \Rightarrow E+i \Rightarrow i+i E+E⇒E+i⇒i+i
E ⇒ ( E ) ⇒ ( E + E ) ⇒ ( E + i ) ⇒ ( E ∗ E + i ) ⇒ ( E ∗ i + i ) ⇒ ( i ∗ i + i ) E \Rightarrow (E) \Rightarrow (E+E) \Rightarrow (E+i) \Rightarrow (E*E+i) \Rightarrow (E*i+i) \Rightarrow (i*i+i) E⇒(E)⇒(E+E)⇒(E+i)⇒(E∗E+i)⇒(E∗i+i)⇒(i∗i+i)
第三章 词法分析器
从正规式构造有限自动机
例3.5 教材P56

NFA确定化
例3.3 教材P50



所用方法:子集法
DFA的化简
例3.6 教材P57



其实非常简单,就是带入输入集看状态是否包含在集合中,如果包含则ok,不包含则分开。
第四章 语法分析-自自上而下分析
消除文法的左递归
例4.2 教材P69

例4.3 教材P70

构造FIRST集和FOLLOW集
例4.7 教材P79
文法4.2:


First集合:能由非终结符号推出的所有的开头符号或可能的ε,但要求这个开头符号是终结符号
- 如果X是终结符,则FIRST(X) = {X}
- 如果X是非终结符,且有产生式形如X → a…,则FIRST(X) = {a}
- 如果X经过一步或多步推导出空字符ε,将ε加入FIRST(X)
- 如果X是非终结符,且有产生式形如X → Y 1 , Y 2 , Y 3 , Y 4 Y_1,Y_2,Y_3,Y_4 Y1,Y2,Y3,Y4…
- Y 1 − Y i − 1 Y_1 - Y_{i-1} Y1−Yi−1均属于非终结符且包含 ε, Y i Y_i Yi为终结符,需要把FIRST( Y i Y_i Yi)除去ε的部分加入到 FIRST(X) 中
- 所有Y都含ε,则把ε加入到FIRST(X)中
Follow集合:紧跟随其后面的终结符号或#
对于文法开始符号S,将#加入到FOLLOW(S)
若A → \rightarrow →αBβ是一个产生式,则将集合FIRST(β)中除ε外的所有元素加入到FOLLOW(B)当中
如果存在一个产生式 A->αB , 或者A->αBβ且FIRST(β)中包含ε , 那么将集合FOLLOW(A)中的所有元素加入到集合FOLLOW(B)中
构造预测分析表
例4.8 教材P79

文法4.2:



分析表M[A,a]的构造
- 对文法G的每个产生式 A → α A \rightarrow \alpha A→α执行下面两步
- 对每个终结符 a ∈ F I R S T ( α ) a \in FIRST(\alpha) a∈FIRST(α),把 A → α A \rightarrow \alpha A→α加到M[A,a]中;
- 若 ε ∈ F I R S T ( α ) \varepsilon \in FIRST(\alpha) ε∈FIRST(α),则对任何 b ∈ F O L L O W ( A ) b \in FOLLOW(A) b∈FOLLOW(A)把 A → α A \rightarrow \alpha A→α加到M[A,b]中。
- 所有无定义的M[A,a]标上出错标志
利用预测分析表进行预测分析
例4.6 教材P78
文法4.2:



第五章 语法分析-自下而上分析
短语、直接短语、句柄
以某非终结符为根的两代以上的子树的所有末端结点从左到右排列就是相对于该非终结符的一个短语
如果子树只有两代,则该短语就是直接短语
句柄:一个句型的最左直接短语
例5.1 教材P85

短语: i 1 , i 2 , i 3 , i 1 ∗ i 2 , i 1 ∗ i 2 + i 3 i_1,i_2,i_3,i_1*i_2,i_1*i_2+i_3 i1,i2,i3,i1∗i2,i1∗i2+i3
直接短语: i i , i 2 , i 3 i_i,i_2,i_3 ii,i2,i3
最左直接短语: i 1 i_1 i1
例5.2 教材P85

FirstVT、LastVT、构造优先关系表
例5.4 教材P90



FIRSTVT§即出现的第一个终结符
- 若 P → a . . . P \rightarrow a... P→a...或 P → Q a . . . P \rightarrow Qa... P→Qa...,则 a ∈ F I R S T V T ( P ) a \in FIRSTVT(P) a∈FIRSTVT(P)
- 若 a ∈ F I R S T V T ( Q ) a \in FIRSTVT(Q) a∈FIRSTVT(Q),且 P → Q . . . P \rightarrow Q... P→Q...,则 a ∈ F I R S T V T ( P ) a \in FIRSTVT(P) a∈FIRSTVT(P)
LASTVT§即出现的最后一个终结符
- 若 P → . . . a P \rightarrow ...a P→...a或 P → . . . a Q P \rightarrow ...aQ P→...aQ,则 a ∈ L A S T V T ( P ) a \in LASTVT(P) a∈LASTVT(P)
- 若 a ∈ L A S T V T ( Q ) a \in LASTVT(Q) a∈LASTVT(Q),且 P → . . . Q P \rightarrow ...Q P→...Q,则 a ∈ L A S T V T ( P ) a \in LASTVT(P) a∈LASTVT(P)
构造优先关系表
- 对于候选形 . . . a P . . . ...aP... ...aP...,则对于任何 b ∈ F I R S T V T ( P ) b \in FIRSTVT(P) b∈FIRSTVT(P),有a<b(<中间带.)
- 对于候选形…Pb…,则对于任何 a ∈ L A S T V T ( P ) a \in LASTVT(P) a∈LASTVT(P),有a>b(>中间带.)



利用LR分析表,写出LR分析器的工作过程
例5.7 教材P102


sn:s表示移进,n表示到第几步
rn:r表示归约,n表示用第几个产生式
LR(0)项目集规范族的构造
构成识别一个文法活前缀的DFA的项目集 (状态)的全体称为文法的LR(0)项目集规范族。
例5.9 教材P107




补充:LR(0)分析表的构造

SLR(1)分析表的构造
LR(0)有移进归约冲突,所以我们引入了SLR

和LR(0)的区别在于,LR(0)一遇到终结符就归约,SLR(1)则是如果输入符号属于FOLLOW集合才归约,从一定程度上减少了移进归约问题
PPT 5.3.3 LR分析法3 P25-31


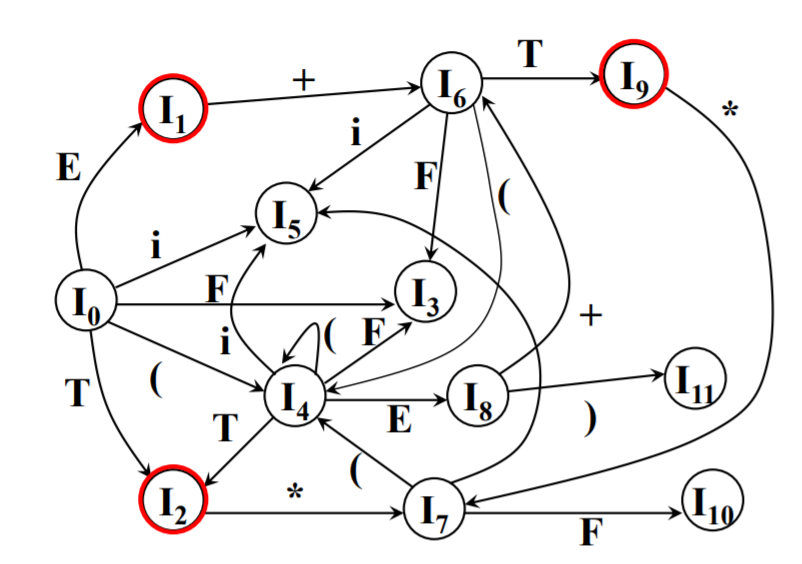



LR(1)项目集族的构造
例5.13 教材P115

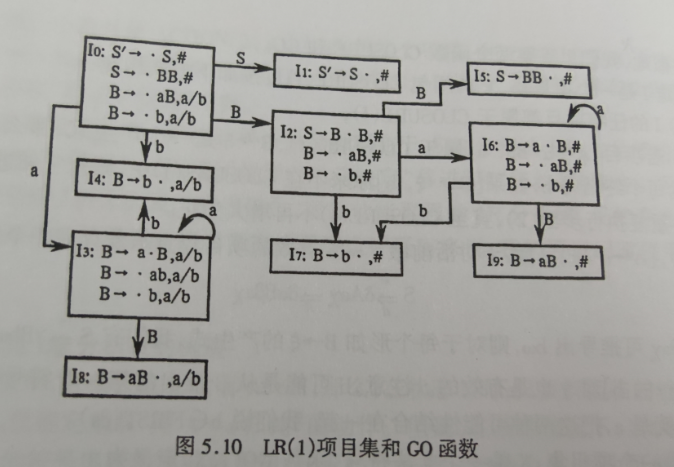
其实就是在LR(0)的基础上往后推一个来判断能否被归约,比如说S→·BB之后的式子,需要满足B之后的一个输入要是B的首符集才能被归约。
我们需要归约的时候,只要对展望串的部分进行归约即可。
LR(1)分析表的构造
PPT 5.3.4 LR分析法4 P22


第六章 属性文案和语法制导翻译
S-属性文法的自下而上计算
例6.9 教材P148


递归下降翻译器的设计
PPT Chapter 6 P60-63




第七章 语义分析和中间代码产生
后缀式

四元式、三元式




说明语句的翻译


赋值语句的翻译

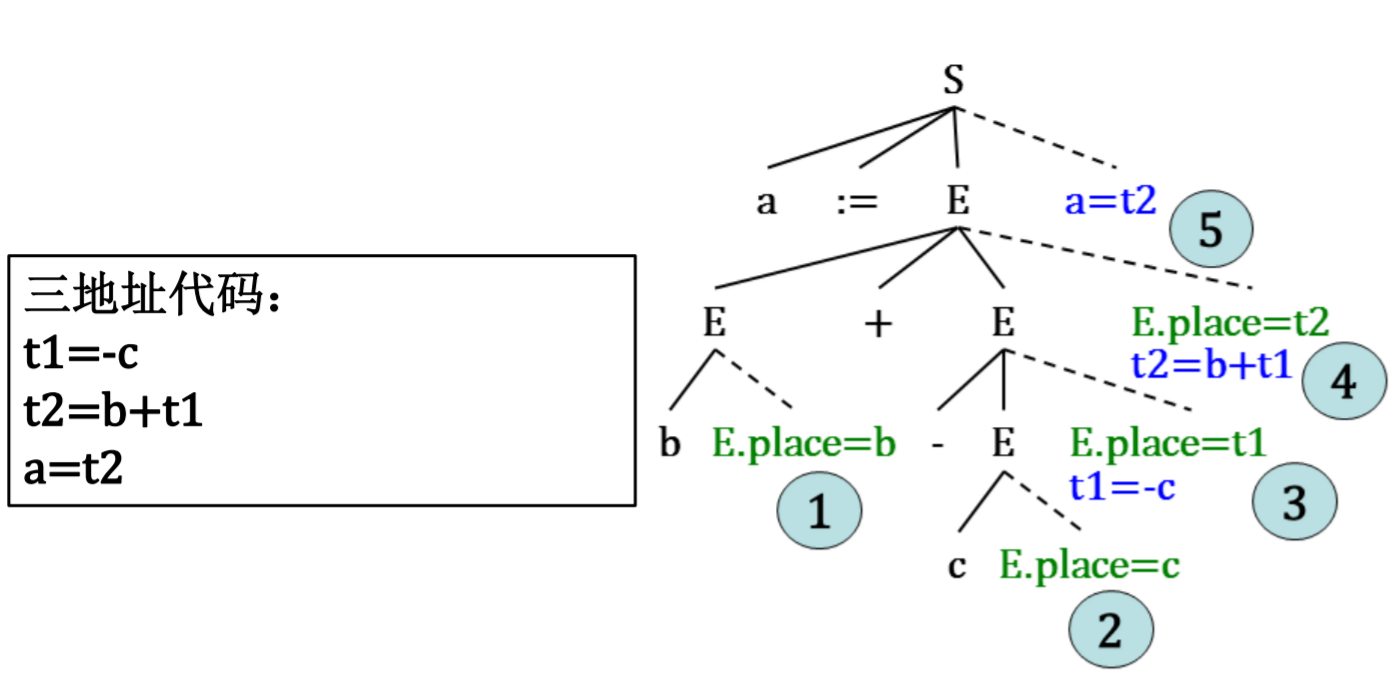
数组元素的引用
例7.1 教材P183

布尔表达式的翻译
例7.4 教材P191


控制语句的翻译
例7.5 教材P194

第十一章 目标代码生成
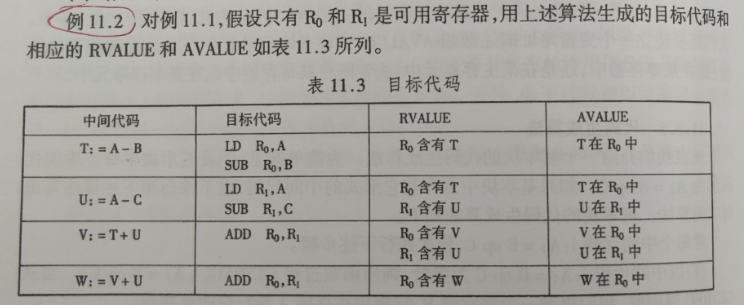
目标代码生成算法
例11.2 教材P316(例11.1 P314)


























 3862
3862

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








