第十一届蓝桥杯——整数拼接

最新推荐文章于 2023-03-01 23:27:58 发布
最新推荐文章于 2023-03-01 23:27:58 发布
阅读量2.8k 收藏 19
点赞数 5
CC 4.0 BY-SA版权
分类专栏： 思维
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_45328552/article/details/108345989
博客详细解析了第十一届蓝桥杯中关于整数拼接的问题，指出暴力解法会超时，并提出优化策略。通过建立表存储乘10的幂次对k取余的结果，减少内层循环的时间复杂度。最后强调了计算中长整型转换和取模防止溢出的重要性，并提示需考虑拼接顺序。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

传送门

 

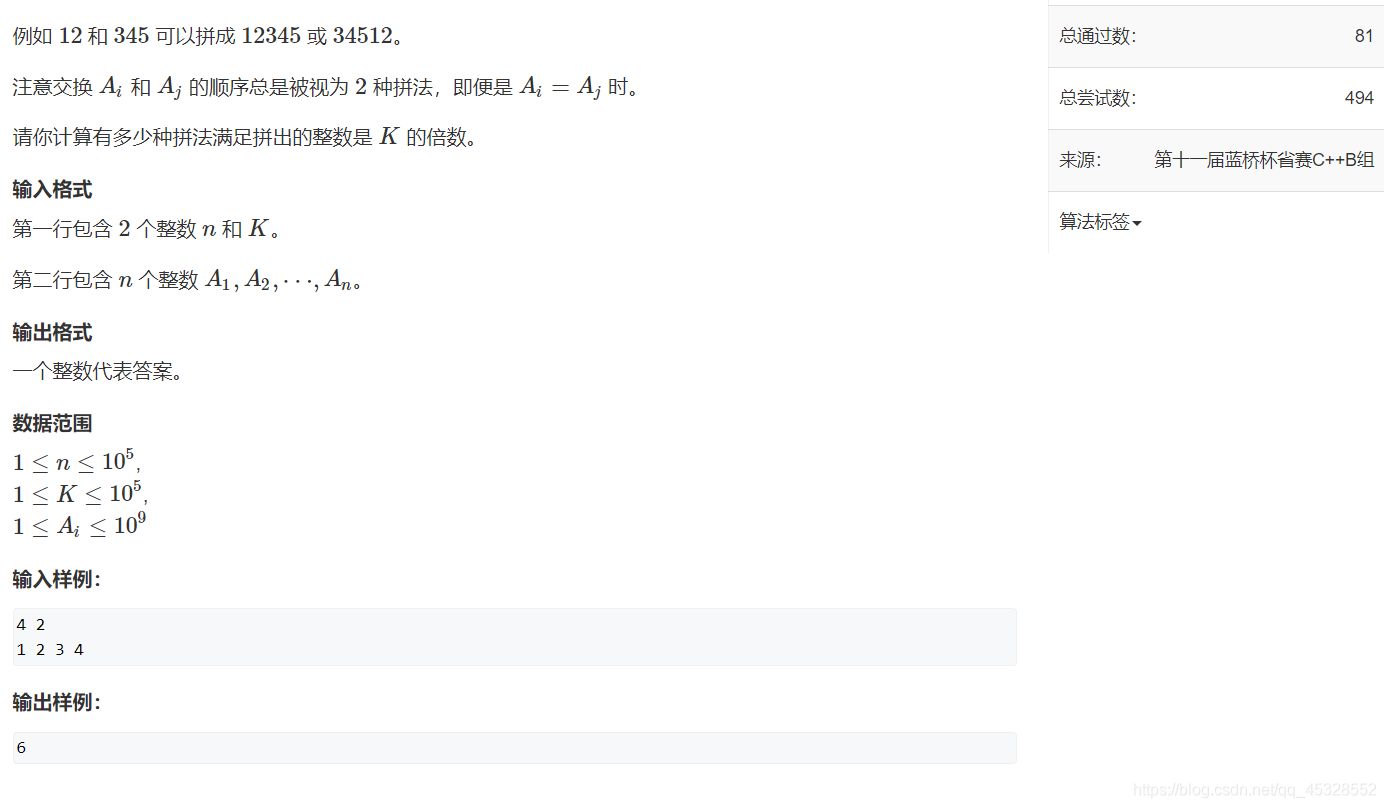
题解：

如果是暴力做法的话，肯定是两个循环遍历一下就行，时间复杂度是O(n^2),但是就这道题而言肯定会超时。

要想计算出有多少种拼法满足两个整数拼出的整数是k的倍数，必须遍历到每一个数，即外层循环必不可少，那如何将内层循环O(n)降下来呢。先将表达式写出来，假如找到两个数Ai和Aj,那么拼出来的数就是Ai*(10^(len(Aj))+Aj,例如12和345拼起来就是12*(10^3)+345,它的余数(Ai*(10^(len(Aj))+Aj)%k就等于((Ai%k*(10^len(Aj)%k))%k + Aj%k)%k.    (len(Aj)表示Aj这个数的长度)

先看前面一项，(Ai%k*(10^len(Aj)%k))%k，由数据范围可知，len(Aj)的长度必然是大于等于1，小于等于10的，而对k取余后，余数肯定小于k的范围，因此数据允许，我们可以建立一张表，用来存放Ai乘10的不同次方（从1到10即可）对k取余的结果的个数，即b[r][(Ai%k*(10^r%k))%k],可知，第一个中括号的r范围是1-10，第二个中括号的范围是小于0-k。

再看第二项Aj%k,如果满足题目条件，那么((Ai%k*(10^len(Aj)%k))%k + Aj%k)%k=0，第一项和第二项的和一定是k（因为两者都小于k），k-Aj%k=(Ai%k*(10^len(Aj)%k))%k,我们如果在上面的表中找到b[len(Aj)][k-Aj%k],证明满足了题目条件，ans++就行。

时间复杂度分析：solve函数外层循环n，内层循环10，log10函数的复杂度为log10(Ai)=9.所以个人

最低0.47元/天 解锁文章

200万优质内容无限畅学
第十一届蓝桥杯C组 试题 J: 整数小拼接
weixin_45741541的博客
09-23 831
时间限制: 1.0s 内存限制: 512.0MB 本题总分：25 分 【问题描述】 给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和 Aj (i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。例如 12 和 345 可 以拼成 12345 或 34512 。注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便 是 Ai = Aj 时。 请你计算有多少种拼法满足拼出的整数小于等于 K。 【输入格式】 第一行包含 2 个整数 n 和 K。
第十三届蓝桥杯大赛青少组——中级组python真题
weixin_51623910的博客
08-10 1763
解析:可以直接暴力，时间复杂度O（N*N*M*M）会超时，预处理二维前缀和，枚举一个起点，然后以这个起点找对角线，找到所有满足条件的对角线，每次找到一个终点，求这个矩形的数据和，如果数据和=正方形的边长，说明其他位置没有1，找到最大的答案即可,时间复杂度为O(N*M*N)。解析：一次可以搬1件，2件，3件，因此要搬k件可以有三类方法，先（k-1）然后1,或者先（k-2），然后2，或者先（k-3）,然后3，用递推就可以了。小马需要将N件物品从河的一岸搬运到河的另一岸，每次搬运的物品为1到3件。
【蓝桥杯】整数拼接
leoyongyuan的博客
03-17 1831
给定一个长度为 n 的数组 A1,A2,⋅⋅⋅,An。 你可以从中选出两个数 Ai 和 Aj(i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。 例如 12 和 345 可以拼成 12345 或 34512。 注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai=Aj 时。 请你计算有多少种拼法满足拼出的整数是 K 的倍数。 输入格式 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1,A2,⋅⋅⋅,An。 输出格式 一个整数代表答案。 数据范围 1≤n≤1
蓝桥杯 整数拼接（思维）
一个小菜鸡的博客
07-18 930
题解看这：https://blog.youkuaiyun.com/weixin_44775484/article/details/107442900 // #pragma GCC optimize(2) #include <iostream> #include <cstdio> #include <algorithm> #include <queue> #include <cmath> #include <string> #i.
蓝桥杯：整数拼接
m0_63613132的博客
03-01 395
adf
整数拼接（蓝桥杯）
weixin_47511190的博客
03-14 604
问题描述 给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和 Aj (i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。例如 12 和 345 可以拼成 12345 或 34512。注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai = Aj 时。请你计算有多少种拼法满足拼出的整数是 K 的倍数。 输入格式 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1, A2, · · · , An。 输出格式 一个整数
蓝桥杯2020年第十一届省赛真题-整数拼接
最新发布
02-11
### 关于蓝桥杯2020年第十一届省赛整数拼接真题 给定长度为 \( n \) 的数组 \( A_1, A_2, \cdots, A_n \)，可以从中选出两个不同的数 \( A_i \) 和 \( A_j \) （\( i \neq j \)），然后将这两个数一前一后拼成一个...
第五届蓝桥杯JavaB组省赛真题
热门推荐
南 墙
07-19 1万+
解题代码部分来自网友，如果有不对的地方，欢迎各位大佬评论 题目1、武功秘籍 小明到X山洞探险，捡到一本有破损的武功秘籍（2000多页！当然是伪造的）。他注意到：书的第10页和第11页在同一张纸上，但第11页和第12页不在同一张纸上。 小明只想练习该书的第81页到第92页的武功，又不想带着整本书。请问他至少要撕下多少张纸带走？ 这是个整数，请通过浏览器提交该数字，不要填写任何多余的内容。 【解析...
蓝桥杯2020年第十一届C/C++B组（第一次）省赛习题题解
lihua777的博客
03-13 3224
蓝桥杯2020年第十一届C/C++B组省赛习题题解
【蓝桥杯】整数小拼接（哈希+二分）
leoyongyuan的博客
03-17 1504
给定一个长度为 n 的数组 A1,A2,⋅⋅⋅,An。 你可以从中选出两个数 Ai 和 Aj(i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。 例如 12 和 345 可以拼成 12345 或 34512。 注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai=Aj 时。 请你计算有多少种拼法满足拼出的整数小于等于 K。 输入格式 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1,A2,⋅⋅⋅,An。 输出格式 一个整数代表答案。 数据范围 1≤n≤10
蓝桥杯---整数拼接
雪岩的博客
03-19 631
整数拼接 问题描述 给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和 Aj (i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。例如 12 和 345 可以拼成 12345 或 34512。注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai = Aj 时。请你计算有多少种拼法满足拼出的整数是 K 的倍数。 输入格式 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1, A2, · · · , An。 输出格式
整数拼接【维度为10的k次方，模数的DP】【蓝桥杯】
谁是凶手1703
10-09 286
整数拼接 题意 给n个整数，从里面选俩个整数，一前一后拼接成一个新数，若这个新数是k的倍数，那么res++。问res多少? 思路 首先暴力代码 for (int i = 0; i < n; i ++ ) for (int j = 0; j < n; j ++ ) if (check(a[i], a[j])) ans ++ ; 第一重循环，去不了的情况下，我们试图优化第二重循环。 第二重循环，求的是：拼接结果a[i] 在前a[j]在后是k的倍数的个
蓝桥杯-整数拼接
Cap07博客
03-29 1323
#include<bits/stdc++.h> using namespace std; long long int getweishu(long long int a) { //获取a是多少位数 long long int num = 0; while (a / 10 != 0) { num++; a = a / 10; } num++; return num; } int main() { int begin1 = 1, begin2 = 1; long lon.
整数拼接（记忆化更新）
qq_43813373的博客
08-19 2065
给定一个长度为 n 的数组 A1,A2,⋅⋅⋅,An。 你可以从中选出两个数 Ai 和 Aj(i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。 例如 12 和 345 可以拼成 12345 或 34512。 注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai=Aj 时。 请你计算有多少种拼法满足拼出的整数是 K 的倍数。 输入格式 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1,A2,⋅⋅⋅,An。 输出格式 一个整数代表答案。 数据范围 1≤n≤1
整数拼接
qq_52413081的博客
02-23 1436
Description 给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和Aj(i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。例如 12 和 345 以拼成 12345 或 34512。注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai = Aj 时。 请你计算有多少种拼法满足拼出的整数是 K 的倍数。 Input 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1, A2, · · · , An。 Out
【十一届蓝桥杯】整数拼接
weixin_46047677的博客
04-04 449
题目链接 ** 根据题意可推出，A与B拼接可以推出等式 A + 10x + B，题目可以翻译成是求A + 10^x + B % K ==0的个数。首先我们肯定不能去枚举两重循环，这样必定会超时， 我们通过观察等式A + 10x + B % K ==0进行等价变形，变成(A + 10^x) % K = - B % K，并且B与x正相关，则我们可以用一个哈希表存起来A +10x，用空间换时间，那么我们的两重循环就可以换成一个只枚举A，调用哈希只需要O(1)的时间，到现在看来题目就迎刃而解了，本题时间复杂度
蓝桥杯 整数小拼接
qq_52385348的博客
02-27 415
【问题描述】 给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和 Aj (i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。 例如 12 和 345 可以拼成 12345 或 34512 。 注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便是 Ai = Aj 时。 请你计算有多少种拼法满足拼出的整数小于等于 K。 【输入格式】 第一行包含 2 个整数 n 和 K。 第二行包含 n 个整数 A1, A2, · · · , An。 【输
蓝桥杯——第十一届省赛——整数小拼接
优快云_765的博客
04-01 591
试题 J: 整数小拼接 本题总分：25 分 【问题描述】 给定义个长度为 n 的数组 A1, A2, · · · , An。你可以从中选出两个数 Ai 和 Aj (i 不等于 j)，然后将 Ai 和 Aj 一前一后拼成一个新的整数。 例如 12 和 345 可以拼成 12345 或 34512 。 注意交换 Ai 和 Aj 的顺序总是被视为 2 种拼法，即便 是 Ai = Aj 时。 请你计算有多少种拼法满足拼出的整数小于等于 K。 【输入格式】 第一行包含 2 个整数 n 和 K。 第
蓝桥杯 python 整数拼接
04-04
题目描述 给定两个正整数 a 和 b，将它们拼接起来得到一个新的整数。 例如，a=12，b=34，则拼接后得到的新整数为 1234。 输入格式 输入共两行，第一行为正整数 a，第二行为正整数 b。两个数字都不超过 10000 位。 输出格式 输出一个整数，表示拼接后的新整数。 样例输入 12 34 样例输出 1234 算法1 (字符串拼接) $O(n)$ 将两个整数转化为字符串，然后将它们拼接起来，最后将拼接后的字符串转化为整数输出即可。 时间复杂度 字符串拼接的时间复杂度为 O(n)，其中 n 表示两个整数的位数。 空间复杂度 需要额外 O(n) 的空间存储字符串。 Python 代码 a = input().strip() b = input().strip() c = int(a + b) print(c) 算法2 (字符串迭代) $O(n)$ 根据题目要求，需要将两个整数拼接起来，可以将两个整数转化为字符串后，通过迭代的方式将两个字符串拼接起来，最后将拼接后的字符串转化为整数输出即可。 时间复杂度 字符串迭代的时间复杂度为 O(n)，其中 n 表示两个整数的位数。 空间复杂度 需要额外 O(n) 的空间存储字符串。 Python 代码 a = input().strip() b = input().strip() c = '' for i in a: c += i for j in b: c += j c = int(c) print(c) 算法3 (数学运算) $O(logn)$ 根据题目要求，需要将两个整数拼接起来，可以通过数学运算实现。 设第一个整数为 a，第二个整数为 b，其位数分别为 len1 和 len2。 将第二个整数 b 乘以 10 ^ len1，然后加上第一个整数 a 即可得到拼接后的结果。 时间复杂度 时间复杂度为 O(logn)，其中 n 表示两个整数的位数。 空间复杂度 只需要额外 O(1) 的空间存储变量。 Python 代码 a = input().strip() b = input().strip() c = int(b) + int(a) * (10 ** len(b)) print(c)
评论 3
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值